软间隔SVM与正则化模型
前面讲到,软间隔SVM对每个数据点记录了其“间隔破坏量”,记为\(\xi_n\),并对该量施加一些惩罚,得到软间隔SVM的优化问题 \[ \begin{align*} \min_{b, {\bf w}}\hspace{2ex}&\frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{n=1}^N \xi_n\\ {\rm s.t.} \hspace{2ex} &y_n({\bf w^\mathsf{T}z}_n + b) \ge 1 -\xi_n,\ \xi_n \ge 0 \forall n \end{align*} \] 这个问题可以使用另一种形式来表示,看看它到底要解决什么事情:给定\(b\)和\(\bf w\),则\(\xi_n\)是怎么算出来的呢?\(\xi_n\)的本质是看这个点对间隔边界的破坏程度,因此对任意一个点,\(\xi_n\)有两种情况
- 这个点的确破坏了间隔边界,因此\(\xi_n\)记录它离想要的数字1有多远,此时\(\xi_n = 1 - y_n({\bf w}^\mathsf{T}{\bf z}_n + b)\)。由于这个点已经破坏了边界,因此\(\xi_n \ge 0\)
- 这个点没有破坏间隔边界,此时\(\xi_n = 0\)
综上所述,\(\xi_n\)可以用一个式子来表示,即\(\xi_n = \max(1 - y_n({\bf w}^\mathsf{T}{\bf z}_n + b), 0)\)。这也意味着软间隔SVM问题可以写成一个没有限制条件的优化问题,为 \[ \min_{b, {\bf w}}\hspace{2ex}\frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{n=1}^N \max(1 - y_n({\bf w}^\mathsf{T}{\bf z}_n + b), 0) \] 此时\(\xi_n\)不再是一个变量,而是一个由\(b\)和\(\bf w\)算出来的结果
这种表示形式和之前讲过的正则化方法非常像:优化问题本身可以分解为两个部分,第一项是\(\bf w\)的长度,代表了模型的复杂度;而第二项可以看做是样本中所有误差的和,这不过这里似乎使用了一种新的误差函数,可以记为\(\widehat{\rm err}\)。但是为什么不能直接解这个问题呢?首先,它不再是一个二次规划问题,因此对偶和核技巧可能不太好用上;其次,\(\max(\cdot, 0)\)并不是处处可微,因此这个优化问题更难解
下表给出了硬/软间隔SVM和正则化模型之间的一些比较
| 模型 | 最小化的目标函数 | 限制条件 |
|---|---|---|
| 带限制条件的正则化 | \(E_{\rm in}\) | \({\bf w^\mathsf{T}w} \le C\) |
| 硬间隔SVM | \(\bf w^\mathsf{T}w\) | \(E_{\rm in} = 0\)(及其他) |
| L2正则化 | \(\frac{\lambda}{N}{\bf w^\mathsf{T}w} + E_{\rm in}\) | |
| 软间隔SVM | \(\frac{1}{2}{\bf w^\mathsf{T}w} + CN\widehat{E_{\rm in}}\) |
即软间隔SVM和L2正则化这两个问题其实非常相似。从上表可知,大间隔其实就是正则化的一种实现,代表可选择的超平面要更少,实际上就是对\(\bf w\)的一种L2正则化;而软间隔则意味着要计算一种特殊的误差函数\(\widehat{\rm err}\)。对于\(C\)来讲,无论是带限制条件的正则化问题还是软间隔SVM问题,\(C\)越大,对应着越小的\(\lambda\),即越小的正则化
把SVM看作是一种正则化模型的好处是,可以将其理论延伸到其他模型,并与这些模型建立联系
SVM vs. Logistic回归
类似于第11讲中的做法,也可以把上面推出的SVM的损失函数\(\widehat{\rm err}_{\rm SVM}\)做出图像,与原始0/1误差函数\({\rm err_{0/1}}(s, y) = [\![ys \not= 1]\!]\)作比较。下图给出了这两个函数的图像
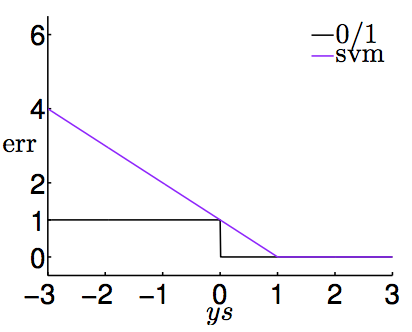
由上图可知,\(\widehat{\rm err}_{\rm SVM}\)是\({\rm err}_{0/1}\)的上界,因此可以用这个上界推导出一些算法,这些算法间接地降低0/1误差,来把0/1分类问题做好。在文献中,SVM使用的这个误差函数通常被称作hinge loss(一些人翻译成“铰链损失函数”)。注意hinge loss不仅是0/1误差函数的上界,还是一个凸的上界,因此在优化时有些好的性质可以利用
接下来再把hinge loss和Logistic回归用的损失函数(经过缩放以后,记为SCE)\(\log_2(1+\exp(-ys))\)做一个比较。当\(ys\)趋近于\(+\infty\)时,\(\widehat{\rm err}_{\rm SVM}(s, y) = 0\);当\(ys\)趋近于\(-\infty\)时,\(\widehat{\rm err}_{\rm SVM} = 1-ys \approx ys\)。而SCE也有类似的结果(只不过是\(ys \rightarrow +\infty\)时,\(\rm SCE \approx 0\)。因此可以说,SVM可以看做是带有L2正则化的Logistic回归
下表对目前讲解过的三种用于0/1分类的模型做了比较
| 模型名称 | 基本思想 | 优点 | 缺点 |
|---|---|---|---|
| PLA | 直接最小化\(\rm err_{0/1}\) | 数据集线性可分时算法效率很高 | 只能用于数据集线性可分的情况,否则就要用口袋算法 |
| 带有正则化的Logistic回归 | 使用GD/SGD最小化正则化的\(\rm err_{SCE}\) | 易于优化,正则化使得模型不易过拟合 | \(ys\)很小时(是很大的负数时)误差函数是0/1误差函数太松的上界 |
| 软间隔SVM | 使用QP最小化正则化的\(\rm \widehat{err}_{SVM}\) | 易于优化,有理论保证 | \(ys\)很小时(是很大的负数时)误差函数是0/1误差函数太松的上界 |
从这个角度来看,带有正则项的Logistic回归其实几乎就是在做SVM。那么当解SVM时,可否将这个解用在Logistic回归中(即估计每个点是正例的概率)?
用作软二元分类的SVM
那么怎么将SVM用在软二元分类问题中呢?一种比较直观的方法是,先使用软间隔SVM算法得到\((b_{\rm SVM}, {\bf w}_{\rm SVM})\),然后使用Logistic函数计算\(\theta({\bf w}_{\rm SVM}^\mathsf{T}{\bf x} + b_{\rm SVM})\),将该结果作为\(g({\bf x})\)的结果返回。这种做法在实际应用中效果还不错,但是失去了之前推导Logistic回归时候用到的最大似然等等思想。另一种方法是,先用SVM算法得到\((b_{\rm SVM}, {\bf w}_{\rm SVM})\),将这个结果作为Logistic回归的初始权重,然后使用Logistic回归算法得到最后的\(g({\bf x})\)。这种方法最后得到的结果跟直接用Logistic回归算法跑出的模型应该差不多,丢失了SVM自己的一些特性,例如核方法等等。因此,这两种简单的做法都不尽如人意,需要想一种办法融合这两个算法的优势
SVM得到的结果如果用\({\bf w}_{\rm SVM}^\mathsf{T}{\boldsymbol{\Phi}({\bf x})} + b_{\rm SVM}\)表示,其本质实际上就是一个分数。接着,对这个分数做缩放和平移,即返回\(g({\bf x}) = \theta(A \cdot ({\bf w}_{\rm SVM}^\mathsf{T}{\boldsymbol{\Phi}({\bf x})} + b_{\rm SVM}) + B)\),通过用Logistic回归训练\(A\)和\(B\)这两个参数来达到使用MLE的目的和效果。由于这个算法的核心还是SVM,因此对偶和核技巧都可以使用。从几何的角度来看,SVM的用处是找到法向量,Logistic回归是使用MLE进行微调。如果\({\bf w}_{\rm SVM}\)比较好,那么\(A > 0, B \approx 0\)
因此,新的Logistic回归问题为 \[ \min_{A,B}\hspace{2ex}\frac{1}{N}\sum_{n=1}^N \log\left(1+\exp\left(-y_n(A\cdot (\underbrace{ {\bf w}_{\rm SVM}^\mathsf{T}{\boldsymbol{\Phi}({\bf x}_n)} + b_{\rm SVM}}_{\boldsymbol{\Phi}_{\rm SVM}({\bf x}_n)}) + B)\right)\right) \] 该问题可以看做是一个两阶段学习问题:先把数据用SVM做一个变换,再用Logistic回归学习两个参数。这个方法称为Platt模型。这种模型,这里称为软二元分类器,的边界和第一步得到的SVM分类器的边界是不太一样的,因为\(B\)的存在会使边界稍微有所移动
这里的做法是先把数据用核方法变换到空间\(\mathcal{Z}\)里,然后用Logistic回归得到一个模型。这种方法并没有直接在\(\mathcal{Z}\)空间里求解Logistic回归,因此并不是该空间里最好的Logistic回归的解。有没有办法真的在这个空间里找到Logistic回归的最优解呢?
核Logistic回归
要使用核方法做Logistic回归,其根本问题是Logistic回归根本就不是一个二次规划问题!但是之前的核方法为什么能管用呢?其基本思想就是把\(\mathcal{Z}\)空间做的内积转化为在\(\mathcal{X}\)空间可以轻易计算的函数。之前提到过,在求解核SVM问题时,不仅在求解\(\bf w_\ast\)时要用到\(\mathcal{Z}\)空间的内积,而在得到最优的\(g\)以后真正预测时,也需要用到\(\mathcal{Z}\)空间的内积。如果最优的\(\bf w_\ast\)可以表达为一堆已经看过的\(\bf z\)的线性组合,那么才能把最后计算\(\bf w_\ast^\mathsf{T}z\)的过程表达为核函数计算的形式。而核SVM能做到这一点,因此核SVM最后有\({\bf w}_\ast^\mathsf{T}{\bf z} = \sum_{n=1}^N\beta_n{\bf z}^\mathsf{T}_n{\bf z} = \sum_{n=1}^N\beta_n K({\bf x}_n, {\bf x})\)。因此,最优解\({\bf w}_\ast\)是一些\({\bf z}_n\)的线性组合,是能用核方法的关键条件
之前讲过的SVM,其最优权重\({\bf w}_{\rm SVM}\)可以写为\({\bf w}_\ast = \sum_{n=1}^N(\alpha_n y_n){\bf z}_n\)这种形式,此时\(\alpha_n\)来自于对偶问题的解。PLA的最优权重实际上也可以写为这种形式,此时\(\alpha_n\)来自于对错分样本的修正。Logistic回归的最优权重也有这样的性质,此时系数由做SGD过程中总共的移动步数决定。换句话说,这三种算法中\(\bf w_\ast\)都可以被\({\bf z}_n\)表示
推而广之,可以先讨论一个更高级的问题:什么时候\(\bf w_\ast\)可以被\({\bf z}_n\)表示?这里可以证明:
对任何带有L2正则化的线性模型
\[ \min_{\bf w}\hspace{2ex}\frac{\lambda}{N}{\bf w^\mathsf{T}w} + \frac{1}{N}\sum_{n=1}^N {\rm err}(y_n, {\bf w^\mathsf{T}z}_n) \]
其最优的\(\bf w_\ast\)都可以被表示为\({\bf z}_n\)的线性组合,即\({\bf w}_\ast = \sum_{n=1}^N \beta_n{\bf z}_n\)。
这个定理称为表示定理。证明如下
将最优的\({\bf w}_\ast\)分解为两个向量\({\bf w}_{||}\)和\({\bf w}_{\perp}\),记由\({\bf z}_n\)张成的空间为\({\rm span}({\bf z}_n)\),\({\bf w}_{||} \in {\rm span}({\bf z}_n), {\bf w}_{\perp} \perp {\rm span}({\bf z}_n)\),即\({\bf w}_\ast = {\bf w}_{||} + {\bf w}_\perp\)。则问题转化为证明在这种分解下有\({\bf w}_{\perp} = {\bf 0}\)。假设\({\bf w}_\perp \not= {\bf 0}\),则由于正交向量的内积为0,有\({\rm err}(y_n, {\bf w_\ast^\mathsf{T}z}_n) = {\rm err}(y_n, ({\bf w_\|} + {\bf w}_\perp)^\mathsf{T}{\bf z}_n) = {\rm err}(y_n, {\bf w_\|^\mathsf{T}z}_n)\),因此\(\bf w_\ast\)和\(\bf w_\|\)有相同的\(\rm err\)。又\({\bf w}_\ast^\mathsf{T}{\bf w}_\ast = {\bf w_\|^\mathsf{T}w_\|} + 2{\bf w_\|^\mathsf{T}w_\perp} + {\bf w_\perp^\mathsf{T}w_\perp} = {\bf w_\|^\mathsf{T}w_\|} + {\bf w_\perp^\mathsf{T}w_\perp} > {\bf w_\|^\mathsf{T}w_\|}\)。这意味着\(\bf w_\|\)比最优解\(\bf w_\ast\)还要使目标函数更小,矛盾!因此肯定有\({\bf w}_\perp = {\bf 0}\),最优解可以用\({\bf z}_n\)的线性组合表示,得证 \(\blacksquare\)
表示定理表明,任何L2正则化的线性模型都可以核化。那么接下来的问题是怎么核化带有L2正则项的Logistic回归。考虑原先问题的定义 \[ \min_{\bf w}\hspace{2ex}\frac{\lambda}{N}{\bf w}^\mathsf{T}{\bf w} + \frac{1}{N}\sum_{n=1}^N \log(1+\exp(-y_n{\bf w}^\mathsf{T}{\bf z}_n)) \] 由表示定理,最优的\({\bf w}_\ast = \sum_{n=1}^N\beta_n{\bf z}_n\)。将该式代入原始问题,可以将原来关于\(\bf w\)的问题转化成关于\(\boldsymbol{\beta}\)的问题,即 \[ \min_{\boldsymbol{\beta}} \frac{\lambda}{N} \sum_{n=1}^N\sum_{m=1}^N\beta_n\beta_m K({\bf x}_n, {\bf x}_m) + \frac{1}{N}\sum_{n=1}^N\log\left(1+\exp\left(-y_n\sum_{m=1}^N\beta_m K({\bf x}_m, {\bf x}_n)\right)\right) \] 这是一个没有条件的最优化问题,因此GD或者SGD方法仍然可以使用
记上面这个问题为KLR问题(Kernel Logistic Regression),可以从另一个角度理解:由前面的讲解,可知核函数从某种意义上也是相似度的一种体现,那么最后一项\(\sum_{m=1}^N\beta_m K({\bf x}_m, {\bf x}_n)\)可以看做是先把所有数据点\({\bf x}_1,\ldots, {\bf x}_N\)与\({\bf x}_n\)的相似度求出来,将这个变换后的数据\(K({\bf x}_1, {\bf x}_n), K({\bf x}_2, {\bf x}_n), \ldots, K({\bf x}_N, {\bf x}_n)\)组成向量与变量\(\boldsymbol{\beta}\)求内积,这其实也是一个小的线性模型。而前面的项\(\sum_{n=1}^N\sum_{m=1}^N \beta_n \beta_m K({\bf x}_n, {\bf x}_m)\)如果写成矩阵形式就是\(\boldsymbol{\beta}^\mathsf{T}{\rm K}\boldsymbol{\beta}\),其本质实际上是一个正则化。即KLR可以看做是一个关于\(\boldsymbol{\beta}\)的线性模型,其对应的\(\bf x\)是用核变换后得到的结果,而正则化也是使用核来做
需要注意的是,KLR与SVM最大的不同为,对KLR,其系数\(\beta_n\)通常都不为0
