核岭回归
由上一讲提到的表示定理可知,任何带有L2正则项的线性模型都能被核化。那么如何把回归模型核化呢?而且回想之前讲岭回归(带有L2正则项的线性回归)时,曾经说过该模型可以得到一个闭合的解析解,那么使用了核方法以后的模型是否能同样有解析解?
首先,将原始岭回归的问题写出 \[ \min_{\bf w}\hspace{2ex}\frac{\lambda}{N}{\bf w^\mathsf{T}w} + \frac{1}{N}\sum_{n=1}^N(y_n - {\bf w^\mathsf{T}z}_n)^2 \] 要使该问题的最优解\({\bf w}_\ast\)可以写作若干个\({\bf z}_n\)的线性组合,即\({\bf w}_\ast = \sum_{n=1}^N \beta_n{\bf z}_n\)。类似于之前KLR的推导,可以把\({\bf w}_\ast\)的表达式代回到原始问题,进而求解最优的\(\boldsymbol{\beta}\)。因此原问题可以化为 \[ \min_{\boldsymbol{\beta}}\hspace{2ex}\frac{\lambda}{N}\sum_{n=1}^N\sum_{m=1}^N\beta_n\beta_mK({\bf x}_n, {\bf x}_m) + \frac{1}{N}\sum_{n=1}^N\left(y_n - \sum_{m=1}^N\beta_mK({\bf x}_n, {\bf x}_m)\right)^2 \] 同样的,第一项可以看做是使用核矩阵\(\rm K\)对\(\boldsymbol{\beta}\)做正则化,第二项是对\(N\)维经核变化过的样本做线性回归,权重为\(\boldsymbol{\beta}\)。经过矩阵/向量化,该问题可以进一步化简为 \[ \min_\boldsymbol{\beta}\hspace{2ex}\frac{\lambda}{N}\boldsymbol{\beta}^\mathsf{T}{\rm K}\boldsymbol{\beta} + \frac{1}{N}(\boldsymbol{\beta}^\mathsf{T}{\rm K^\mathsf{T}K}\boldsymbol{\beta} - 2\boldsymbol{\beta}^\mathsf{T}{\rm K}^\mathsf{T}{\bf y} + {\bf y^\mathsf{T}y}) \] 将上式对\(\boldsymbol{\beta}\)取梯度,同时注意\(\rm K\)是对称矩阵(Mercer定理),可知\({\rm K = K^\mathsf{T} = K^\mathsf{T}I}\)。因此 \[ \nabla E_{\rm aug}(\boldsymbol{\beta}) = \frac{2}{N}(\lambda {\rm K^\mathsf{T}I}\boldsymbol{\beta} + {\rm K^\mathsf{T}K}{\boldsymbol{\beta}} - {\rm K^\mathsf{T}}{\bf y}) = \frac{2}{N}{\rm K^\mathsf{T}((\lambda{\rm I+K})\boldsymbol{\beta} - {\bf y})} \] 可知最后也可以得到\(\boldsymbol{\beta}\)的解析解为\(\boldsymbol{\beta} = (\lambda {\rm I +K})^{-1}{\bf y}\),返回的\(g({\bf x}) = \sum_{n=1}^N \beta_nK({\bf x}_n, \bf x)\)。由于\(\rm K\)是半正定矩阵且\(\lambda >0\),因此\(\lambda {\rm I + K}\)总是可逆的。求解该问题的时间复杂度为\(O(N^3)\)。相比而言,线性岭回归得到的结果\({\bf w}={\rm (\lambda I + X^\mathsf{T}X)^{-1}X^\mathsf{T}}{\bf y}\)更受限(如果不做多项式变换,只能得到线性模型),但是训练时间复杂度\(O(d^3 +d^2N)\),预测时间复杂度\(O(d)\),在\(N >\!> d\)时效率更高。核岭回归尽管得到的模型更灵活,但是训练时间复杂度\(O(N^3)\),预测时间复杂度\(O(N)\),不适合处理大的数据集。这再次说明我们通常要在模型的灵活性和计算效率之间进行权衡
支持向量回归的原始问题
前面说到,线性回归(及其带正则化的变种)也可以用来解决分类问题。使用了核方法的核岭回归也可以解决同样的问题,此时这个模型被称为最小二乘支持向量机(Least-Squares SVM, LSSVM)。高斯LSSVM和软间隔高斯核SVM的对比可见下图

可见两者的边界差别不是很大,但是对LSSVM,几乎所有点都是支持向量,而对软间隔SVM,只有少数点是支持向量。支持向量越多,预测的时间就越长,效率就越低。那么有没有办法得到这样一种模型:它既可以解决回归问题,又可以像标准SVM那样有稀疏的\(\boldsymbol{\beta}\)呢?
首先考虑一个“管道回归”问题(tube regression):之前讲线性回归的时候,对模型误差的判定非常严苛:对某个点\(({\bf x}_n, y_n)\),只有当它完全落在学习出的超平面上时,它的误差才是0。只要出现一点偏差,就要负责任。但是在管道回归问题里,错误评判的标准宽松了一些:在标线的基础上,拓展出来一部分“中立区”。即便是某些点没有落在超平面上,只要落在中立区里,误差就不计算了。对于落在中立区外的点,其误差计算也不是看它到超平面的距离,而是看它离中立区的距离。下图给出了一个示例
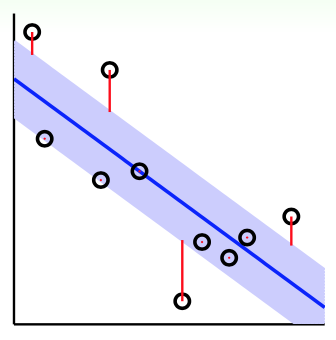
上图中,蓝色线是学习出的超平面,蓝色带是划分出的“中立区”,红线表明了各点误差的大小。假设中立区的(单侧)高度为\(\epsilon\),管道回归的误差函数为 \[ {\rm err}(y, s) = \max(0, |s-y|-\epsilon) \] 可以看出,这个误差函数(通常称为\(\epsilon\)-不敏感误差)与前面讲到的SVM的hinge loss形式很像。而如果将此误差函数的图像做出来,可以发现当\(|y-s|\)比较小时,管道回归的误差与平方误差大致相等。\(|y-s|\)比较大时,管道回归的误差又远小于平方误差,这说明前者受离群点的影响更小
接下来要做的就是求解这个带有L2正则项的管道回归问题来得到一个稀疏的\(\boldsymbol{\beta}\)。首先将问题描述出来 \[ \min_{\bf w}\hspace{2ex}\frac{\lambda}{N}{\bf w^\mathsf{T}w} + \frac{1}{N}\sum_{n=1}^N\max\left(0, |{\bf w^\mathsf{T}z}_n-y|-\epsilon\right) \] 尽管这是一个无限制条件的优化问题,但是\(\max\)函数不是处处可微的,因此使用微分的方法会遇到问题。标准SVM也有类似的问题,但是重写为一个QP问题以后就好解了。此外,为了使用核方法,该问题可以用表示定理来转换为一个可核化的问题,但是可能不会有稀疏性的保证;而标准SVM由于有对偶问题和KKT条件,有稀疏性的保证。因此在求解此问题时,也会试着像QP、对偶和KKT条件靠拢。所以接下来仿照标准SVM问题对原问题进行重写 \[ \min_{b, {\bf w}}\hspace{2ex}\frac{1}{2}{\bf w^\mathsf{T}w} + C\sum_{n=1}^N\max(0, |{\bf w^\mathsf{T}z}_n+b-y_n|-\epsilon) \] 原始软间隔SVM问题对\(\max\)函数的处理是引入了边界破坏量\(\xi_n\)。这里使用了类似的思想,但是由于绝对值符号的存在,只引入一个\(\xi_n\)是不够的,约束条件还不是一个线性问题。应该将绝对值符号展开,并引入两个量:向下惩罚项\(\xi_n^\lor\)和向上惩罚项\(\xi_n^\land\)。这样一来,就得到了标准支持向量回归(SVR)的原始问题,形式为 \[ \begin{align*} \min_{b, {\bf w}, \boldsymbol{\xi}^\lor, \boldsymbol{\xi}^\land}\hspace{2ex}&\frac{1}{2}{\bf w^\mathsf{T}w} + C\sum_{n=1}^N(\xi_n^\lor + \xi_n^\land) \\ {\rm s.t.}\hspace{2ex}& -\epsilon - \xi_n^\lor \le y_n - {\bf w^\mathsf{T}z}_n - b \le \epsilon + \xi_n^\land \\ &\xi_n^\lor \ge 0, \xi_n^\land \ge 0 \end{align*} \] 这里各参数的意义为
- \(C\)在正则的程度和对管道的破坏程度中做均衡
- \(\epsilon\)控制管道在竖直方向上的宽度(比原来SVM多出来一个超参数)
这个QP问题有\(\tilde{d}+1+2N\)个变量,\(2N+2N\)个限制条件
支持向量回归的对偶问题
要写出上述原始问题的对偶问题,第一步是引入拉格朗日乘子。记约束条件\(y_n - {\bf w^\mathsf{T}z}_n - b \le \epsilon + \xi_n^\land\)对应的拉格朗日乘子为\(\alpha_n^\land\),约束条件\(-\epsilon - \xi_n^\lor \le y_n - {\bf w^\mathsf{T}z}_n - b\)对应的拉格朗日乘子为\(\alpha_n^\lor\)。经过类似第18讲和20讲的一些计算,可以得到以下一些KKT条件 \[ \begin{align*} \frac{\partial \mathcal{L}}{\partial w_i} = 0&\Rightarrow {\bf w} = \sum_{n=1}^N(\alpha_n^\land - \alpha_n^\lor){\bf z}_n \\ \frac{\partial \mathcal{L}}{\partial b} = 0 & \Rightarrow \sum_{n=1}^N(\alpha_n^\land - \alpha_n^\lor) = 0 \end{align*} \] 以及其中的互补松弛条件为 \[ \begin{cases} \alpha_n^\land(\epsilon + \xi_n^\land - y_n + {\bf w^\mathsf{T}z}_n + b) = 0 \\ \alpha_n^\lor(\epsilon + \xi_n^\lor + y_n - {\bf w^\mathsf{T}z}_n - b) = 0 \end{cases} \] 最终可以得到对偶问题为 \[ \begin{align*} \min \hspace{2ex} &\frac{1}{2}\sum_{n=1}^N\sum_{m=1}^N(\alpha_n^\land - \alpha_n^\lor)(\alpha_m^\land - \alpha_m^\lor)K({\bf z}_n, {\bf z}_m) + \sum_{n=1}^N((\epsilon-y_n)\cdot \alpha_n^\land + (\epsilon + y_n)\cdot \alpha_n^\lor) \\ {\rm s.t.} \hspace{2ex} &\sum_{n=1}^N(\alpha_n^\land - \alpha_n^\lor) = 0 \\ &0 \le \alpha_n^\land \le C, 0\le \alpha_n^\lor \le C \end{align*} \] 这个问题也可以用二次规划求解器求解
最后,由前面的KKT条件可知\({\bf w} = \sum_{n=1}^N (\alpha_n^\land - \alpha_n^\lor){\bf z}_n\)。记\(\alpha_n^\land - \alpha_n^\lor\)为\(\beta_n\),要证明的就是\(\beta_n\)组成的系数向量\(\boldsymbol{\beta}\)是稀疏的。由前面的互补松弛条件,对那些在管道中的点,其对应的\(\xi_n^\land\)和\(\xi_n^\lor\)都为0。由于此时有\(|{\bf w}^\mathsf{T}{\bf z}+b-y_n|<\epsilon\),因此互补松弛条件中\(\epsilon + \xi_n^\land - y_n + {\bf w^\mathsf{T}z}_n + b\)和\(\epsilon + \xi_n^\lor + y_n - {\bf w^\mathsf{T}z}_n - b\)都不为0,也就是它们对应的\(\alpha_n^\land\)和\(\alpha_n^\lor\)都为0,\(\beta_n\)也就为0。所以可以得出结论:落在管道边界上或管道外的数据点才对\(\bf w\)有贡献,它们才是支持向量,\(\boldsymbol{\beta}\)是稀疏的
核模型总结
最后对前面讲过的所有线性模型和使用了核技巧的模型(简称核模型)做一总结,参见下图
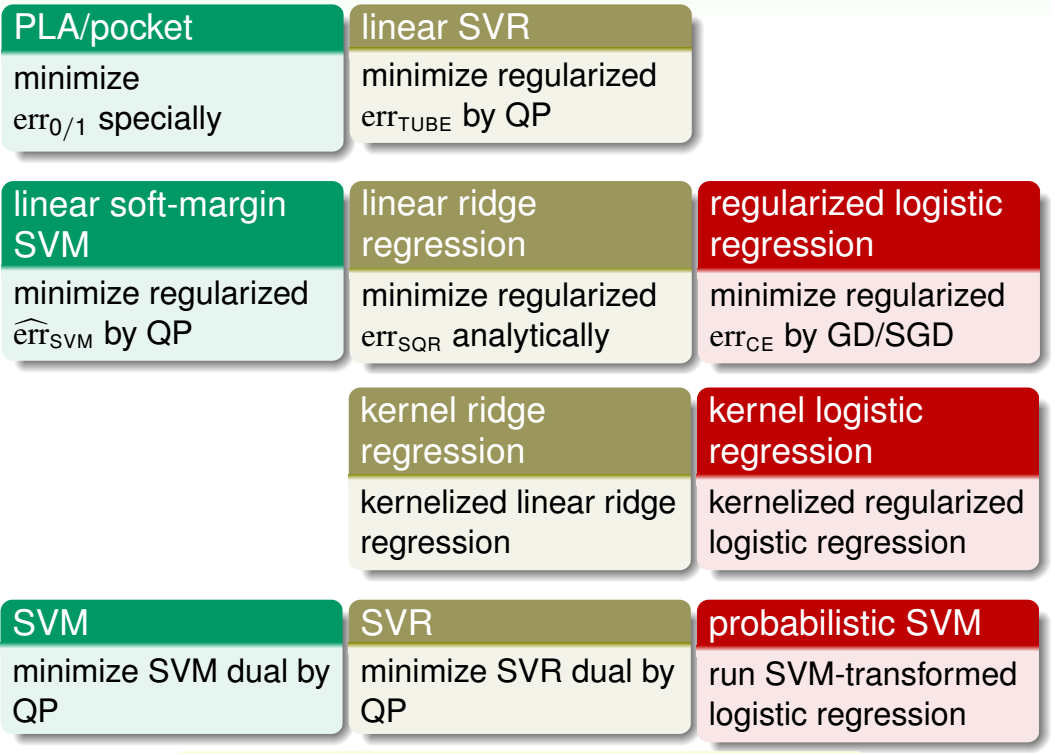
上图中,
- 前两行均为线性模型,其中
- 第一行较少使用,因为性能/效果比较差
- 第二行是经典机器学习包liblinear的主力
- 后两行均为核模型,其中
- 第三行较少使用,因为支持向量是稠密的
- 第四行是经典机器学习包libsvm的主力
核模型中可用的核包括多项式核、高斯核,或者是任何满足Mercer条件的自定义核。它们是线性模型的有力扩展。但是“能力越大责任越大”,使用这些强力模型时,要更小心地调参以及做验证,避免过拟合现象的出现
