动机与原始问题
上一讲最后提到,SVM也会出现过拟合的情况。那么在什么时候SVM会过拟合呢?其中一种情况是使用太强力的\(\boldsymbol{\Phi}\),而另一种情况是坚持认为数据是完全可分的。回顾之前的理论,如果总是坚持要完全可分输入数据,就是要找到一个\(g\)使得输入数据可以被\(g\)打散,因此也就增大了过拟合的可能性
回想之前介绍的口袋算法,这个算法对那些线性不可分的数据集做了一些退让:不再要求得到的超平面可以完全分开已知数据,但求最优超平面犯的错误越少越好,即口袋算法得到的\(b, {\bf w}\)满足 \[ \min_{b, {\bf w}}\sum_{n=1}^N [\![y_n \not= {\rm sign}({\bf w^\mathsf{T}z}_n + b)]\!] \] 相比而言,前面提到的硬间隔SVM的条件实在是太苛刻了:不仅要求每个样本都分对,还要求每个样本离分离超平面有一定的距离。因此,可以适当放松要求,让它对错分的样本不再施加到超平面的距离限制,只控制错分样本的数目让其越少越好(即不让模型无止境地犯错)。这样,得到的优化问题变成了 \[ \begin{align*} \min_{b, {\bf w}}\hspace{2ex}&\frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{n=1}^N [\![y_n \not= {\rm sign}({\bf w^\mathsf{T}z}_n + b)]\!] \\ {\rm s.t.} \hspace{2ex} &y_n({\bf w^\mathsf{T}z}_n + b) \ge 1 {\rm\ for\ correct\ }n \\ &y_n ({\bf w^\mathsf{T}z}_n + b) \ge -\infty{\rm\ for\ incorrect\ }n \end{align*} \] 这里\(C\)控制了在训练集上准确性和间隔大小这两者之间的平衡。\(C\)越大,越倾向于不要再训练集上犯错误;\(C\)越小,越倾向于在正确分类的数据上分类器间隔尽可能大
上述问题可以对表达形式做一步化简,得到一个等价的问题 \[ \begin{align*} \min_{b, {\bf w}}\hspace{2ex}&\frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{n=1}^N [\![y_n \not= {\rm sign}({\bf w^\mathsf{T}z}_n + b)]\!] \\ {\rm s.t.} \hspace{2ex} &y_n({\bf w^\mathsf{T}z}_n + b) \ge 1 -\infty\cdot [\![y_n \not= {\rm sign}({\bf w^\mathsf{T}z}_n + b)]\!] \end{align*} \] 注意这个问题的限制条件里有\(N\)个布尔表达式\([\![\cdot]\!]\),因此不是线性约束,整个问题不能再用二次规划求解器来求解,之前的对偶方法、核方法也就没法做了。而且“预测错”也有两种错误的方法,一种是离边界很近的错误,一种是离边界很远的错误,这个问题也没法区分这两种错误,因此需要对这个问题进行修改。一种修改方法是对每个数据点引入\(\xi_n\)这个变量,表示分类器在这个数据点上犯的错误的严重性。最优化问题里要优化的问题也不再简单记录“犯了多少错误”,而是记录所有数据点总共犯错误的情况。即要求解的问题和约束为如下形式 \[ \begin{align*} \min_{b, {\bf w}}\hspace{2ex}&\frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{n=1}^N \xi_n\\ {\rm s.t.} \hspace{2ex} &y_n({\bf w^\mathsf{T}z}_n + b) \ge 1 -\xi_n,\ \xi_n \ge 0 \forall n \end{align*} \] 这样一来,所有约束条件都是线性约束,要求解的目标问题是二次函数,又可以用QP求解器求解了。这种问题称为软间隔支持向量机,其中\(\xi_n\)记录的是数据点的“间隔破坏程度”,如下图所示
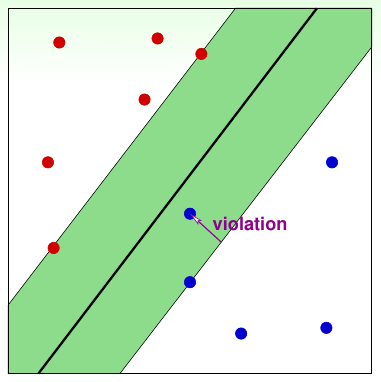
上面描述的问题中,\(C\)越大,表示对错误的容忍程度越小,对所有点尽可能不错分;\(C\)越小,表示对错误的容忍程度越大,要求的间隔越宽
新的问题有\(\tilde{d} + 1 + N\)个变量,有\(2N\)个约束条件。接下来,就要用对偶问题来移除问题对\(\tilde{d}\)的依赖
对偶问题
对原始问题 \[ \begin{align*} \min_{b, {\bf w}}\hspace{2ex}&\frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{n=1}^N \xi_n\\ {\rm s.t.} \hspace{2ex} &y_n({\bf w^\mathsf{T}z}_n + b) \ge 1 -\xi_n,\ \xi_n \ge 0 \forall n \end{align*} \] 可以看到对每个点都有两个约束条件。引入拉格朗日乘子\(\alpha_n\)和\(\beta_n\),可以得到拉格朗日函数 \[ \begin{align*} \mathcal{L}(b, {\bf w}, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\beta}) = &\frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{n=1}^N \xi_n \\ & +\sum_{n=1}^N \alpha_n\cdot (1-\xi_n - y_n({\bf w^\mathsf{T}z}_n + b)) + \sum_{n=1}^N \beta_n \cdot (-\xi_n) \end{align*} \] 对应的对偶问题可以写为 \[ \begin{align*} \max_{\alpha_n \ge 0, \beta_n \ge 0} \left(\min_{b, {\bf w}, \boldsymbol{\xi}} \frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{n=1}^N \xi_n +\sum_{n=1}^N \alpha_n\cdot (1-\xi_n - y_n({\bf w^\mathsf{T}z}_n + b)) + \sum_{n=1}^N \beta_n \cdot (-\xi_n)\right) \end{align*} \] 解这个问题可以用第18讲中相同的技巧:最优的\(\boldsymbol{\xi}\)必然满足\(\frac{\partial \mathcal{L}}{\partial \xi_n} = 0\),因此可以先解这个关系式 \[ \frac{\partial \mathcal{L}}{\partial \xi_n} = 0 \Rightarrow C - \alpha_n-\beta_n = 0 \] 因此可以把\(\beta_n\)换掉,即\(\beta_n = C - \alpha_n\),并施加一个写明的约束条件\(0 \le \alpha_n \le C\)。将\(\beta_n\)的这个表达式代入到上面的对偶问题,可以消掉\(\beta_n\)和\(\xi_n\),问题转化为 \[ \max_{0\le \alpha_n \le C, \beta_n = C-\alpha_n}\left(\min_{b, {\bf w}} \frac{1}{2}{\bf w^\mathsf{T}w} + \sum_{n=1}^N \alpha_n\cdot (1-y_n({\bf w^\mathsf{T}z}_n + b)) \right) \] 这个问题和第18讲中推出的对偶问题非常相近,只是最外部\(\alpha_n\)的条件有细微差别。利用同样的方法可以推出 \[ \begin{align*} \frac{\partial \mathcal{L}}{\partial b} = 0 &\Rightarrow \sum_{n=1}^N\alpha_ny_n = 0 \\ \frac{\partial \mathcal{L}}{\partial {\bf w}} = 0 &\Rightarrow {\bf w} = \sum_{n=1}^N\alpha_ny_n{\bf z}_n \end{align*} \] 因此,软间隔SVM对偶问题的标准形式为 \[ \begin{align*} \min_{\boldsymbol{\alpha}} \hspace{2ex}&\frac{1}{2}\sum_{n=1}^N\sum_{m=1}^N \alpha_n\alpha_m y_ny_m{\bf z}_n^\mathsf{T}{\bf z}_m - \sum_{n=1}^N\alpha_n \\ {\rm subject\ to} \hspace{2ex}&\sum_{n=1}^Ny_n\alpha_n = 0; \\ & 0 \le \alpha_n \le C, {\rm for\ }n=1,2,\ldots,N \end{align*} \] 与前面硬间隔SVM对偶问题的标准形式的唯一区别就是这里\(\alpha_n\)有了上限\(C\)。这也是一个标准的二次规划问题,有\(N\)个变量,\(2N+1\)个限制条件
软间隔SVM传递的信息
得到软间隔SVM对偶问题的标准形式以后,求解这个问题的步骤与第18讲硬间隔SVM对偶问题的求解步骤基本类似(如果引入核方法,那么就把在高维空间算内积的步骤用核函数代替)。由于\(C\)和\(\xi_n\)的存在,软间隔SVM不再像硬间隔SVM那样数据必须线性可分时才能有解,而是总有解的。因此软间隔SVM是一种更灵活的模型,在实践中是最常用的SVM模型
接下来的问题是软间隔SVM如何求解\(b\),因为这两个毕竟是不同的QP问题,KKT条件不完全相同。对于软间隔SVM,其互补松弛条件(complementary slackness)为 \[ \begin{align*} \alpha_n(1-\xi_n - y_n({\bf w^\mathsf{T}z}_n + b)) &= 0 \\ \beta_n(-\xi_n) &= 0 \end{align*} \] 将前面推出的\(\beta_n\)的关系式代入,有 \[ \begin{align*} \alpha_n(1-\xi_n - y_n({\bf w^\mathsf{T}z}_n + b)) &= 0 \\ (C-\alpha_n)\xi_n&= 0 \end{align*} \] 假设\(\alpha_s > 0\),即\(s\)是一个支持向量,由第一个式子,可以求出 \[ b = y_s - y_s\xi_s - {\bf w^\mathsf{T}z}_s \] (注意这里用到了\(y_s\)的一个特点:因为\(y_s \in \{-1, +1\}\),因此任意数除以\(y_s\)与乘以\(y_s\)的效果是一样的)
这里带了一个惩罚项,如果要算出\(\xi_s\),就得先算出\(b\),造成了一个鸡生蛋蛋生鸡的问题。因此要看第二个式子,如果\(\alpha_s < C\),那么就会有\(\xi_s = 0\)。这种\(0 < \alpha_s < C\)的支持向量称为自由的支持向量。综上所述,使用任意自由的支持向量\(({\bf x}_s, y_s)\),都可以求出唯一的\(b\)为 \[ b = y_s - \sum_{ {\rm SV\ indices\ }n} \alpha_ny_nK({\bf x}_n, {\bf x}_s) \] 当然,极少数的情况下,没有自由的支持向量,那么\(b\)就只能通过一系列不等式得出,此时可能有不止一个\(b\)存在
软间隔SVM(使用高斯核)的例子如下图所示。可以看到,小的\(C\)可能会有欠拟合,而大的\(C\)仍然会导致过拟合的现象。因此,对软间隔SVM,仍然要小心地选择\((\gamma, C)\)

由前面的互补松弛条件,可以看到不同的数据点对应的\(\alpha_n\)可以分为三种
- 非支持向量,\(\alpha_n = 0, \xi_n = 0\) 。这种点被正确分类,且远离分离超平面的间隔边界
- 自由支持向量,\(0 < \alpha_n < C, \xi_n = 0\) 。这种点被正确分类,骑在分离超平面的间隔边界上,决定\(b\)值
- 受限的支持向量,\(\alpha_n=C\) 。这种点的\(\xi_n = 1-y_n({\bf w^\mathsf{T}z}_n + b)\),肯定越过了间隔边界。这种店如果要分还能分成两种:一种是跨过了间隔边界,但是没跨过分离超平面;还一种是已经跨过了分离超平面
这三种点可见下图示意。其中自由支持向量以方框圈出,受限的支持向量以三角圈出

模型选择
前面说过,对高斯SVM(之后提到SVM都默认是软间隔SVM+核方法),不同的\((C, \gamma)\)都会产生不同的分隔边界。到底怎样的组合才是最好的?还是要用交叉验证的方法来选择
这里着重观察交叉验证中最特殊的一种交叉验证:留一交叉验证(LOOCV)。由前面的讲解,可知在训练样本数为\(N\)的情况下,LOOCV可以看做是N折交叉验证。这里要证明的一点是:
对于SVM,有 \[ E_{\rm LOOCV} \le \frac{\#{\rm SV}}{N} \]
证明如下:
假设对\(({\bf x}_N, y_N)\),解出来最优的\(\alpha_N=0\),则该点不是支持向量。因此,如果把这个点从原始数据集中除去,剩下的\((\alpha_1, \alpha_2, \ldots, \alpha_{N-1})\)仍然是剩下的数据集按照算法求出来的最优的\(\boldsymbol{\alpha}\)。也就是说,在LOOCV时如果去掉的是非支持向量点,那么得到的\(g^-\)和不去掉这个点得到的\(g\)是一样的。考虑到非支持向量点肯定是被正确分类,且远离边界的点,因此有 \[ \begin{align*} e_{\rm non-SV} &= {\rm err}(g^-, {\rm non\text{-}SV}) \\ &= {\rm err}(g, {\rm non\text{-}SV}) = 0 \end{align*} \] 对支持向量,有\(e_{\rm SV} \le 1\)
将这些式子都加起来求平均,可知 \[ E_{\rm LOOCV} \le \frac{\# {\rm SV}}{N} \] \(\blacksquare\)
这意味着似乎可以通过支持向量的数量来判断SVM算法是否过拟合。如果一个算法的支持向量数比较少,那么它过拟合的风险可能就比较小。但是实际应用时,有这么几点需要注意
\({\#{\rm SV}}(C, \gamma)\)是\((C, \gamma)\)一个不平滑的函数,因此很难优化
\(\#{\rm SV}\)只是\(E_{\rm LOOCV}\)的上界,并非确界
因此,如果在调参时太耗时间,可以先干掉一些支持向量数太多的模型,然后再去仔细验证剩下的模型
