核技巧
前面提到,对偶问题最后也能写成二次规划问题的标准形式。乍一看,问题的变量数为\(N\),条件数为\(N+1\),跟数据的维度\(\tilde{d}\)无关,但是需要注意的是,\(\rm Q_D\)中的每一项计算方式为两个\(y\)相乘再乘上两个\(\bf z\)的内积(\(q_{n, m} = y_ny_m{\bf z}_n^\mathsf{T}{\bf z}_m\)}),这个内积就跟\(\tilde{d}\)有关了。如果数据维度很大,那么\(\rm Q_D\)的计算量就很大,成为了求解问题的瓶颈所在。如果使用某种技巧把\({\bf z}_n^\mathsf{T}{\bf z}_m\)这个直接做内积步骤替换掉,那么计算效率就能得到比较大的提升
经过进一步分析可以发现,之前的讨论都是在\(\mathcal{Z}\)空间做的。但是\(\bf z\)实际上是原始数据\(\bf x\)经过非线性变换\(\boldsymbol{\Phi}\)得到,因此求\({\bf z}_n^\mathsf{T}{\bf z}_m\)实际上是两步:先做变换,再内积。这两个步骤如果能合起来,是不是计算会快一点?
先从一个比较简单的例子入手:考虑之前提到的二次多项式变换 \[ \boldsymbol{\Phi}_2({\bf x}) = (1, x_1, x_2, \ldots, x_d, x_1^2, x_1x_2, \ldots x_1x_d, x_2x_1, x_2^2, \ldots ,x_2x_d, \ldots, x_d^2) \] 这里为了简单起见,将\(x_1x_2\)和\(x_2x_1\)都放了进来。接下来,假设有两个数据点\(\bf x\)和\(\bf x'\),看一看先转换再做内积的结果,有 \[ \begin{align*} \boldsymbol{\Phi}_2({\bf x})^\mathsf{T}\boldsymbol{\Phi}_2({\bf x}') &= 1 +\sum_{i=1}^dx_ix_i' + \sum_{i=1}^d\sum_{j=1}^dx_ix_jx_i'x_j' \\ &= 1+\sum_{i=1}^dx_ix_i' + \sum_{i=1}^d x_ix_i'\sum_{j=1}^dx_jx_j' \\ &= 1 + {\bf x}^\mathsf{T}{\bf x}' + ({\bf x}^\mathsf{T}{\bf x}')({\bf x}^\mathsf{T}{\bf x}') \end{align*} \] 化简以后,\(\boldsymbol{\Phi}_2({\bf x})^\mathsf{T}\boldsymbol{\Phi}_2({\bf x}')\)的计算复杂度从\(O(d^2)\)降到了\(O(d)\)。因此,在某些情况下,如果把变换和内积这两个步骤合起来,计算效率可以得到提高。这里可以把转换+内积这个合并步称为核函数,即对变换\(\boldsymbol{\Phi}\)有对应的核函数\(K_\boldsymbol{\Phi}\)满足 \[ K_\boldsymbol{\Phi}({\bf x}, {\bf x}') \equiv \boldsymbol{\Phi}({\bf x})^\mathsf{T}\boldsymbol{\Phi}({\bf x}') \] 在本例中,有 \[ \boldsymbol{\Phi}_2 \Leftrightarrow K_{\boldsymbol{\Phi}_2}({\bf x}, {\bf x}') = 1 + ({\bf x}^\mathsf{T}{\bf x}') + ({\bf x}^\mathsf{T}{\bf x}')^2 \] 有了核函数以后,原始对偶SVM的算法可以有如下几点修改
矩阵\(\rm Q_D\)中的每一项\(q_{n, m}\)的计算得到了简化:\(q_{n, m} = y_ny_m {\bf z}_n^\mathsf{T}{\bf z}_m = y_ny_mK({\bf x}_n, {\bf x}_m)\)。注意这里给核函数传递的是在原始空间\(\mathcal{X}\)的向量,提出核函数也就是为了避免在高维空间的计算
计算最优的偏置\(b\)时,也会用到。具体为(注意\({\bf w}= \sum_{n=1}^N \alpha_n y_n {\bf z}_n\)) \[ b = y_s - {\bf w}^\mathsf{T}{\bf z}_s = y_s - \left(\sum_{n=1}^N \alpha_ny_n{\bf z}_n\right)^\mathsf{T}{\bf z}_s = y_s - \sum_{n=1}^N \alpha_ny_n\left(K({\bf x}_n, {\bf x}_s)\right) \] 这里\(({\bf x}_s, y_s)\)是得到的任意一个支持向量
类似地,得到最优的\({\bf w}\)和\(b\)以后,对新的测试输入\(\bf x\),也可以引入核函数来做预测 \[ g_{\rm SVM}({\bf x}) = {\rm sign}({\bf w}^\mathsf{T}\boldsymbol{\Phi}({\bf x}) + b) = {\rm sign}\left(\sum_{n=1}^N \alpha_ny_nK({\bf x}_n, {\bf x}) + b\right) \]
可以注意到,原有对偶问题求解的时候,里面所有要在\(\tilde{d}\)维空间\(\mathcal{Z}\)做的操作,最后都可以在\(d\)维空间\(\mathcal{X}\)通过核函数\(K\)得到相等的结果。这种方法也称为“核技巧”,即把所有转换-内积的步骤都换成计算核函数的值,因此在算法里就不会依赖\(\tilde{d}\)了
引入核函数以后,就可以得到核硬边界SVM算法(Kernel Hard-Margin SVM Algorithm)
\(q_{n,m} = y_ny_m K({\bf x}_n, {\bf x}_m); {\bf p} = -{\bf 1}_N\) (\(\rm A\)和\(\bf c\)还是对偶硬边界SVM算法中的对应值)
\(\boldsymbol{\alpha} \leftarrow {\rm QP}({\rm Q_D}, {\bf p}, {\rm A}, {\bf c})\)
任选一个支持向量\(({\bf x}_s, y_s)\),计算\(b \leftarrow \left(y_s - \sum_{\rm SV\ indices}\alpha_ny_nK({\bf x}_n, {\bf x}_s)\right)\)
将所有支持向量、对应的\(\alpha_n\)和\(b\)返回。对新的\(\bf x\),计算 \[ g_{\rm SVM}({\bf x}) = {\rm sign}\left(\sum_{\rm SV\ indices}\alpha_ny_nK({\bf x}_n, {\bf x})+b\right) \]
假设核函数的计算时间为\(k\),则算法中第一步的时间复杂度仅为\(O(kN^2)\),第二步只有\(N\)个变量和\(N\)个限制条件,第三、四步的时间复杂度为\(O(k\#{\rm SV})\)。因此可以看到,引入核函数以后,就可以完全避免在\(\tilde{d}\)维空间做计算,而且核SVM的预测还是只需要支持向量就可以
多项式核
除去上一节给出的变换,还有其它一些比较常见的二次多项式变换方法,例如 \[ \begin{align*} \boldsymbol{\Phi}_2({\bf x}) = (1, \sqrt{2}x_1, \ldots, \sqrt{2}x_d, x_1^2, \ldots, x_d^2) &\Leftrightarrow K_{2'}({\bf x}, {\bf x}') = 1 + 2{\bf x^\mathsf{T}x}'+({\bf x^\mathsf{T}x}')^2 \\ \boldsymbol{\Phi}_2({\bf x}) = (1,\sqrt{2\gamma}x_1, \ldots, \sqrt{2\gamma}x_d, \gamma x_1^2, \ldots, \gamma x_d^2) &\Leftrightarrow K_2({\bf x}, {\bf x}') = 1 + 2\gamma{\bf x^\mathsf{T}x}' + \gamma^2({\bf x^\mathsf{T}x}')^2 \\ &= (1+\gamma{\bf x^\mathsf{T}x}')^2 \hspace{3ex} (\gamma > 0) \end{align*} \] 可以看到\(K_2\)的计算比\(K_{\boldsymbol{\Phi}_2}\)更简单一些,而能力相同(两者映射到的空间相同)。但是要注意的是,转换不同,内积就不同。内积不同,距离就不同。而SVM是由距离决定的,因此会得到不同的边界。实际上\(K_2\)更常用
下图中给出了使用不同的核和同一个核使用不同\(\gamma\)的效果。其中带方框的点是支持向量
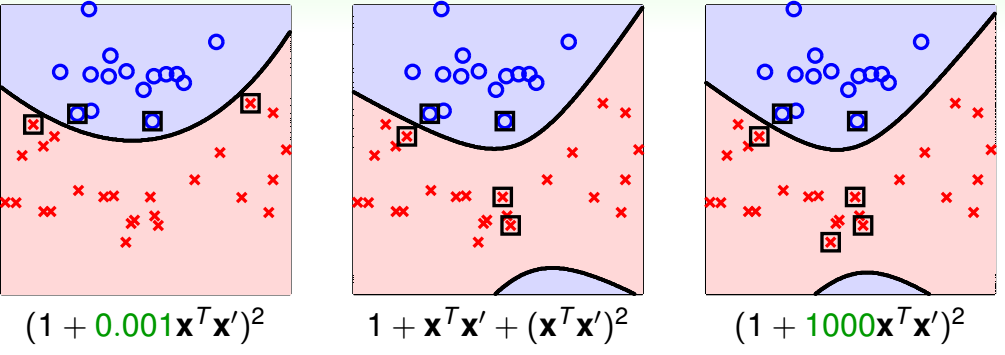
由上图可知,不同的\(g_{\rm SVM}\)会使用不同的支持向量,也就会产生的不同的边界。而使用什么核和\(\gamma\)也是很难在学习之前就能判断出来的。究竟哪个核,这个核的哪个\(\gamma\)最合适,也得通过交叉验证的方法来判断
进一步地,可以加入两个新的变量\(\zeta\)和多项式次数\(Q\),得到一个更广义的多项式核,即(均设定\(\gamma > 0, \zeta \ge 0\)) \[ \begin{align*} K_2({\bf x}, {\bf x}') &= (\zeta + \gamma {\bf x^\mathsf{T}x}')^2 \\ K_3({\bf x}, {\bf x}') &= (\zeta + \gamma {\bf x^\mathsf{T}x}')^3 \\ &\vdots \\ K_Q({\bf x}, {\bf x}') &= (\zeta + \gamma {\bf x^\mathsf{T}x}')^Q \end{align*} \] 这说明,原来的\(Q\)次多项式变换\(\boldsymbol{\Phi}_Q\)在引入参数为\((\zeta, \gamma)\)的核以后,可以得到相同的效果。而核函数的计算方法又使得不再需要将经过\(\boldsymbol{\Phi}_Q\)变换得到的\(\bf z\)展开,极大加快了计算效率。这种将SVM和多项式核结合起来的方法称为多项式SVM
多项式核里比较特殊的一种是\(\zeta=0, \gamma = 1, Q=1\)。这种核称为线性核。尽管高次多项式核非常强大,但是真正实验模型时还是应该先从线性核这种简单模型试起
高斯核
由上一节可知,如果设计一个很好的核函数,则可以使用\(O(d)\)的时间复杂度计算原始数据被映射到\(\tilde{d}\)维空间以后的内积。那么有没有可能有这么一种核函数,使得可以很方便地计算无限维空间的内积呢?的确存在这么一种核函数。接下来的推导中,为了方便起见,假设\(\bf x\)只有一个维度,记为\(x\),则 \[ \begin{align*} K(x, x') &= \exp(-(x-x')^2) \\ &= \exp(-(x)^2)\exp(-(x')^2)\exp(2xx') \\ &= \exp(-(x)^2)\exp(-(x')^2)\left(\sum_{i=0}^\infty\frac{(2xx')^i}{i!}\right) \hspace{3ex}{\rm Taylor\ expansion} \\ &= \sum_{i=0}^\infty\left(\exp(-(x)^2)\exp(-(x')^2)\sqrt{\frac{2^i}{i!}}\sqrt{\frac{2^i}{i!}} (x)^i(x')^i\right) \\ &= \boldsymbol{\Phi}(x)^\mathsf{T}\boldsymbol{\Phi}(x') \end{align*} \] 即多项式变换 \[ \boldsymbol{\Phi}(x) = \exp(-x^2)\cdot \left(1, \sqrt{\frac{2}{1!}}x, \sqrt{\frac{2^2}{2!}}x^2,\ldots\right) \] 可以把\(x\)映射到一个无限维空间,而在该空间两个元素的内积可以在原始空间很方便地使用高斯函数求解。更普遍性地,称形如 \[ K({\bf x}, {\bf x}') = \exp\left(-\gamma |\!|{\bf x} - {\bf x}'|\!|^2\right), {\hspace{3ex}}\gamma>0 \] 这样的核函数为高斯核
将高斯核的表示代入到核SVM中,可以得到使用高斯核的SVM的形式 \[ \begin{align*} g_{\rm SVM}({\bf x}) &= {\rm sign}\left(\sum_{\rm SV}\alpha_ny_n K({\bf x}_n, {\bf x})+b\right) \\ &= {\rm sign}\left(\sum_{\rm SV}\alpha_ny_n \exp\left(-\gamma|\!|{\bf x}-{\bf x}_n|\!|^2\right)+b\right) \end{align*} \] 此时SVM实际上是以各支持向量\({\bf x}_n\)为中心的高斯函数的线性组合。考虑到“线性组合”的意义,高斯核通常也称为径向基函数核(Radial Basis Function kernel, RBF kernel)。高斯核函数的使用进一步展示了核SVM的强大:不需要太多的数据点(仅使用支持向量),也不需要太多的计算(仅在原始\(d\)维空间做向量运算),就能得到特别复杂的边界(因为高斯核实际上隐含地将原始数据映射到了无限维空间),而且很鲁棒(SVM本身最大边界的性质)。核函数的简洁性使得我们也不需要去显式地把转换\(\boldsymbol{\Phi}\)写出来,对偶SVM的性质使得我们不需要去存储最优的\(\bf w\),只需要存好哪些是支持向量以及这些支持向量对应的\(\alpha_n\)就可以
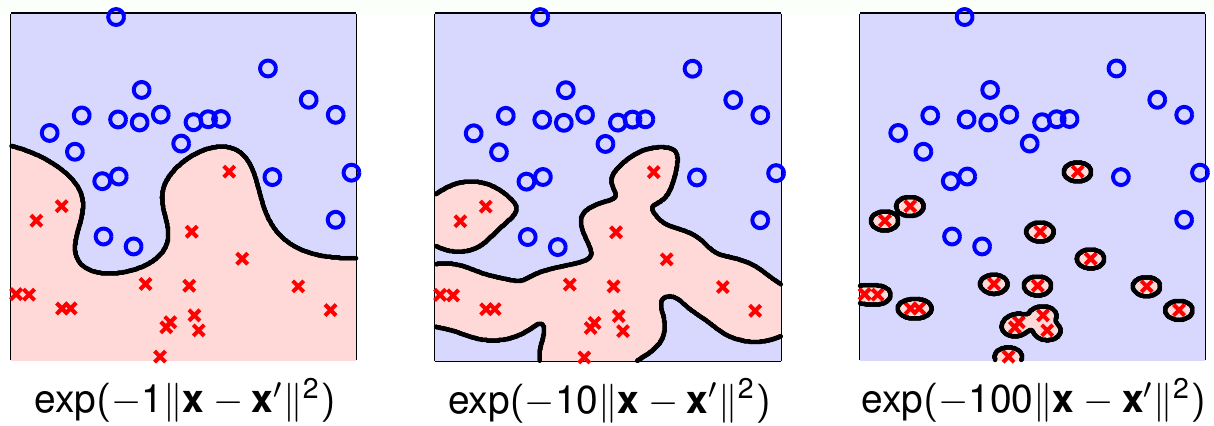
上图给出了使用不同\(\gamma\)的高斯核SVM的示意图。可以看出,\(\gamma\)越大,对应的高斯函数越尖锐,模型越容易过拟合。这里也说明SVM是不容易过拟合,但是不会永远不过拟合。使用高斯核时,\(\gamma\)的选取仍然是需要仔细考虑的。当\(\gamma\rightarrow \infty\)时,如果\(K\)是高斯核函数,则\(K({\bf x, x}') = [\![{\bf x} = {\bf x}']\!]\)
核的比较
本讲一共介绍了三种常见的核,下面对它们做一比较
- 最简单的线性核\(K({\bf x, x}') = {\bf x^\mathsf{T}x}'\)实际上没有对原始数据做任何变化。这种核最简单最安全,而且最快(直接对原始问题用QP求解器求解)。最后得到的模型解释性也比较强,\(\bf w\)会给出每个特征的权重,支持向量会给出每个数据点的重要性。其坏处是可用的场景比较有限,数据并不总是线性可分的。然而无论如何,线性核都是最简单直接的工具,应该在最开始的时候就试用一下
- 多项式核\(K({\bf x}, {\bf x}') = (\zeta + \gamma {\bf x^\mathsf{T}x}')^Q\)的好处是可用场景比线性核要广泛,而且工程师可以通过限制\(Q\)的大小来对模型的复杂度加以控制。其坏处是当\(Q\)比较大时,如果\(|\zeta + \gamma {\bf x^\mathsf{T}x}'| < 1\)则核函数值会逼近0,如果\(|\zeta + \gamma {\bf x^\mathsf{T}x}'| > 1\)则核函数值会非常大。总体来讲,数值计算会不太稳定。而且,这个模型里有三个参数\((\gamma, \zeta, Q)\),调参也比较困难。因此,多项式核可能仅适用于\(Q\)比较小的场景,而且在这种情况下有时反而把\(\boldsymbol{\Phi}({\bf x})\)展开然后代入到线性核求解效率更高
- 高斯核\(K({\bf x}, {\bf x}') = \exp\left(-\gamma |\!|{\bf x} - {\bf x}'|\!|^2\right)\)可以算出最复杂的边界,而且由于其值域为\((0, 1]\),计算稳定性也比较高,不会出现浮点数计算的上溢和下溢。这个核函数只有一个参数\(\gamma\)可调,也比较容易调参。但是由于它把原始数据映射到无限维空间,因此没有一个直观的\(\bf w\)可以用来解释模型。它的计算也比线性核慢,也更容易过拟合。总体来讲,高斯核是一种最常用的核函数,但是用的时候一定要小心
当然,还可以使用其它核函数。从本质上看,核函数实际上是相似性的某种度量方式,其度量的是\(\bf x\)和\(\bf x'\)经过变换以后在空间\(\mathcal{Z}\)中的相似性。那么所有相似性都能用一个合法的核函数来表示呢?并非总是如此。给定函数\(K\),令\(k_{ij} = K({\bf x}_i, {\bf x}_j)\),则矩阵\(\rm K\)必须同时满足以下两个条件(充要条件),\(K\)才是合法的核函数。这两个条件包括
- \(\rm K\)是对称的
- \(K\)必须是半正定的
这个条件称为Mercer条件
自定义核是可能的,不过需要注意的是,也是很难的
额外的话
我大概算了算,这应该是我第五遍听关于SVM的课了(吴恩达Coursera课、吴恩达CS229、白思理哥伦比亚大学EdX课、林轩田课x2)。如果算上看pluskid大神、JerryLead大神两神的文章,SVM的理论我不知道过了多少遍。但是遗憾的是,一是由于我天性驽钝,二是因为我有学而不思的毛病,关于“核方法”这个概念,我每次都是很快拾起,然后更快忘记。这次重听林轩田老师的课,我决定努力从各个方面试着战胜自己一次。其中之一就是试着写一点自己关于核方法的理解,让自己能多思考一点,进而把核方法这个概念和思想留在脑子里的时间延长一些,+ns
既然是自己理解的,肯定会有这样那样的问题。欢迎在知乎专栏里指正
首先一点,核方法是一个独立的方法。大部分课程在讲授核方法的时候,都会在讲SVM时引入它。相比较而言,白思理的课程更微妙一些,是先讲核再讲SVM。所以我觉得核方法和SVM的关系应该是这样:核方法提供了一种在低维空间对向量做计算的方式,通过这种方式计算出来的结果,与通过某种映射将原始向量映射到高维空间以后在高维空间做内积的结果是一致的。SVM的对偶问题里计算\(\rm Q\)时、根据支持向量计算\(b\)时以及对新的\(\bf x\)计算估计值\(\hat{y}\)时,都有高维空间计算内积的需求,而这个计算恰好能用核函数在原始空间计算的结果替代,如此而已。更简单地说,是SVM可以用到核方法,而不是SVM产生了核方法
其次一点,在很多讲核SVM的讲义里,都可以看到类似这样的写法(事实上,在林的课件里,就有类似的写法): \[ K\langle{\bf x}, {\bf x}'\rangle = \boldsymbol{\Phi}({\bf x})^\mathsf{T}\boldsymbol{\Phi}({\bf x}') \] 初学者最开始看到这个式子的时候,不知道会不会像驽钝的我一样,开始好奇一些其实不用好奇的问题,例如:
- 尖角符号代表了什么意义啊?
- 这个对应的\(\boldsymbol{\Phi}\)应该是怎样的啊?
- 映射了以后的那个高维空间\(\mathcal{Z}\)应该是什么样的啊?
在这里我试着回答以前的我一下
- 尖角符号没毛意义,写成\(K({\bf x}, {\bf x}')\)这种普通函数的形式一点问题都没有。核方法的核心是核函数,核函数,归根到底,还是函数,就是给你两个向量,定义一种计算方法,没了。值得玩味的是,这种计算方法里一般会有原始向量的内积运算。多项式核里这个内积是写在明面上的,高斯核稍微不那么明显,但是考虑两点:首先,\(|\!|{\bf v}|\!|^2 = {\bf v^\mathsf{T}v}\),其次,看上面展开计算的式子,其实也有内积的影子
- \(K\)对应的\(\boldsymbol{\Phi}\)和\(\mathcal{Z}\)是什么样的,这个在理论证明提出的核函数有效时可能应该需要分析,但是如果只站在应用层面,我觉得是不用太关心的。事实上,提出核函数的目的就是为了避免直接像高维空间的变换和在高维空间的计算,如果问题使得我们必须要提出一个自定义的核函数,证明时只需要证明 1. 这个新的核函数确实好用 2. 这个核函数满足Mercer条件,可能就可以了。另外,讲义中给出了\(K\)对应的矩阵\(\rm K\),我甚至怀疑在证明\(\rm K\)是半正定的时候,也不需要把所有\(\boldsymbol{\Phi}({\bf x}_i)^\mathsf{T}\boldsymbol{\Phi}({\bf x}_j)\)都列出来放在一个大的矩阵里,肯定有其它更抽象的证明方法
所以最后再唠叨一句,核方法的意义就在于,我们只需要关心核函数\(K\)是什么样的就行,它后头的\(\boldsymbol{\Phi}, \mathcal{Z}\)都是透明的了
