本讲使用了CS231n的讲义,而这份讲义非常详细,这里只做一个简单的笔记。所有插图的链接都链到了原始讲义的图片地址
卷积神经网络,又被称为CNN或者ConvNet。这种体系结构直接假设输入是图片(原文如此,实际上某些文本问题也可以用CNN处理),并直接将一些性质编码在了体系结构中。而且,CNN可以显著减少参数数量,因此计算更高效
体系结构概览
常规神经网络的所有隐藏层神经元都与前面一层的所有神经元全连接,这种做法不是很适合处理图像。假设输入图像宽200像素、高200像素,有3个颜色通道,那么第一个隐藏层就有\(200 \times 200 \times 3 = 120,000\)个权重需要训练,权重太多容易过拟合
一般来说,CNN会分成若干层,这些层可能属于不同类型,完成不同功能。CNN中常见的层大致可以属于以下类型:卷积层、池化层、ReLU层和全连接层。成熟的CNN体系结构(例如AlexNet、VGGNet等)都是将这些层组合起来的产物。每一层接受一个三维的输入,通过一个可微函数将其转化成一个三维的输出。其中卷积层和全连接层有参数(可以理解为权重,会随反向传播而更新)而ReLU和池化层没有,卷积层、全连接层和池化层都有额外超参数可以调节,ReLU层没有
卷积层(CONV)
卷积层是CNN的核心组成部分,是减少计算量的关键所在
基本概念
卷积层的参数由一组可学习的滤波器组合,每个滤波器的宽度和高度都比较小,不过与输入有相同的深度。例如,CNN的第一层所用的滤波器通常大小为\(5 \times 5\times 3\),也就是5像素宽,5像素高,3通道。在正向传播时,把每个滤波器沿着输入的宽和高滑动,计算滤波器和输入对应区域的点积(实际上更准确地说,是做了一个卷积操作)。在这个滑动的过程中,可以生成一个二维的激活映射,给出这个滤波器在每个点上的回应。直觉上来看,网络学习到的滤波器会在看到某种视觉特征的时候被激活
网络在每个卷积层都会学习若干个滤波器,然后沿着深度的维度将它们堆叠起来。如果从神经科学的角度看,输出的每个元素都可以理解为是某个神经元的输出。该神经元只观察输入的一个很小的区域,然后将参数共享给“左边”和“右边”的神经元。神经元看的区域的大小,也就是之前提到的滤波器的尺寸。这个尺寸是一个超参数,也被称作是神经元的感受野。注意滤波器的深度通常与输入的深度相同
前面讲述的是卷积层与输入的连通性,接下来说一下其与输出的连通性。这里一共有三个超参数来控制:深度、步幅(stride)和补零(zero-padding)
- “深度”定义了要使用多少滤波器。每个滤波器对同一输入内容(就是前面说的那个“很小的区域”)的关注点可能不一样
- “步幅”定义每次将滤波器滑动多少像素
- 有时,需要在图像周围补0,这样可以控制输出的空间大小(就是宽和高的乘积)
这样,输出的空间大小可以看作是一个关于输入大小\(W\)、神经元感受野大小\(F\)、步幅大小\(S\)和补零数量\(P\)的函数。具体值为 \[
{\rm output\_size} = \frac{W-F+2P}{S} + 1
\] 
上图给出了对一维数据的卷积结果。灰色代表输入,\(W=5, P=1, F=3\)。左边给出的是\(S=1\)的情况,中间给出的是\(S=2\)的情况。注意\(S\)不能设为3,因为此时\(W-F+2P = 4\)不能被3整除(所以补零很大程度上是为了解决这种问题)。右边给出了神经元的权重(\(1 \times 0 + 0\times 1+2\times(-1) = -2\),以此类推)
通常情况下,\(S=1\)时,\(P\)被设置为\((F-1)/2\),这样可以使得输出大小和输入大小相等。具体原因后面解释
参数共享
CNN崭露头角的第一年,2012年问世的AlexNet接受的图片大小为\(227 \times 227 \times 3\),第一层卷积层的感受野大小\(F=11\),步幅\(S=4\),深度\(K=96\)。由上面的计算可知卷积层输出的大小是\(55 \times 55 \times 96\),每个神经元都连接到一块\(11 \times 11 \times 3\)的输入。如果没有参数共享的话,那么这意味着\(55 \times 55 \times 96 = 290,400\)个神经元每一个都有\(11 \times 11 \times 3 = 363\)个权重和1个偏置,因此第一个卷积层就会有\(290,400 \times 364 = 105,705,600\)个参数,实在是太大了
对于这样的问题,可以做一个合理假设来显著减少参数数量:如果某个特征对计算某个空间位置\((x,y)\)有效果,那么它计算另一位位置\((x_2,y_2)\)应该也有效果。也就是说,对关注同一层深度的神经元,可以让它们享有同样的权重和偏置。这样,第一个卷积层的参数个数会降低到\(96 \times (11 \times 11 \times 3 + 1) = 34,944\)。不过,如果输入的图像有某些特殊的结构,例如要做脸部识别时,需要学出关于眼睛或者头发的特征,那么这种参数共享的方法就会出现问题。应对方案是放松限制,将这一层转化为局部连接层
总而言之,卷积层
- 接受的输入大小为\(W_1 \times H_1 \times D_1\)
- 由4个超参数配置
- 滤波器数量\(K\)
- 感知野大小\(F\)
- 步幅\(S\)
- 补零数量\(P\)
- 产生的输出大小为\(W_2 \times H_2 \times D_2\),其中
- \(W_2 = (W_1 - F + 2P) / S+1\)
- \(H_2 = (H_1 - F + 2P)/S+1\)
- \(D_2 = K\)
- 每个滤波器有\(F \times F \times D_1\)个权重
- 输出的第\(d\)个切片是使用第\(d\)个滤波器在输入上以步幅\(S\)做合法卷积,然后以第\(d\)个偏置的大小做出偏移的结果
实现
由于卷积的核心就是滤波器和输入某块区域的点乘,因此卷积层的正向传播操作通常实现为大矩阵的乘积。具体做法为
- 将输入图像的各个局部区域拉伸成若干列。例如假设输入大小是\(227 \times 227 \times 3\),滤波器大小为\(11 \times 11 \times 3 = 363\),步幅为4,那么输出的大小为\((227 - 11) / 4 + 1 = 55\)。整个图像就会被拉伸成一个\(363 \times 3025\ (55 \times 55 = 3025)\)的矩阵
X_col,每一列都是一个感受野 - 卷积层的权重被拉伸为行。假设有96个滤波器,那么得到的权重矩阵
W_row的大小为\(96 \times 363\) - 卷积操作实际上就是
np.dot(W_row, X_col) - 得到的矩阵大小为\(96 \times 3025\),需要再被调整到正确的维度\(55 \times 55 \times 96\)
其它细节
1x1 卷积:一些论文使用的是\(1\times 1\)的卷积核,这种做法由Network in Network这篇论文率先引入。如果输入的深度为\(d\),这相当于做一个\(d\)维的点乘(笔者注:看知乎上的相关讨论,这种做法一般会伴随着深度的改变,从而也达到一些降维的效果。可参考 这篇导览型的文章 )
空洞卷积(dilated convolution):Multi-Scale Context Aggregation by Dilated Convolutions为卷积层引入了一个新的超参数,称为空洞(dilation,或译为膨胀)。具体的讨论可以参考这篇知乎回答
池化层(POOL)
通常会在两个卷积层之间插入一个池化(pooling)层,来减小表示的空间大小,这样可以减少参数数量和计算量,控制过拟合。最常见的操作是在深度这个维度上,对每个切片使用大小为\(2\times 2\)的滤波器,以跨度2来求最大值,这样可以将75%的激活值都砍掉(\(2\times 2\)的区域上只保留一个值)。下图右边给出了一个例子
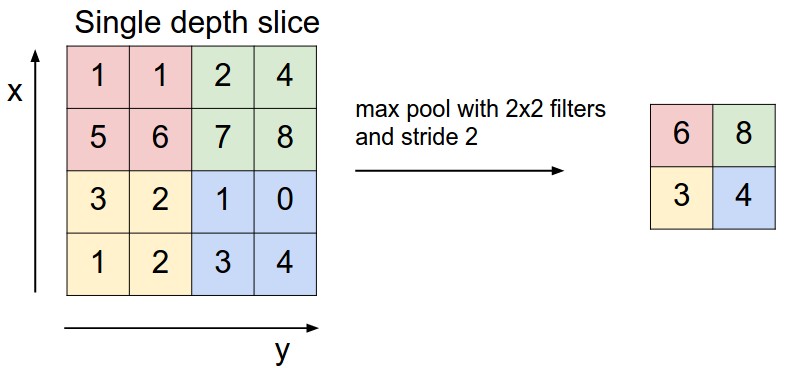
总体来讲,池化层
- 接受的输入大小为\(W_1 \times H_1 \times D_1\)
- 由两个超参数配置
- 滤波器大小\(F\)
- 步幅\(S\)
- 产生的输出大小为\(W_2 \times H_2 \times D_2\)
- \(W_2 = (W_1 - F) / S+1\)
- \(W_2 = (H_1 - F) / S + 1\)
- \(D_2 = D_1\)
- 由于池化操作是一个固定函数,因此不引入参数。此外,池化通常不需要补零
实践中通常只有两种配置:\(F=3, S=2\)或\(F=2, S=2\)。不建议使用太大的滤波器。除了最大池化,还可以使用平均池化和L2-范数池化,不过最大池化的效果实践显示最好。一些研究人员不喜欢池化操作,建议在卷积层使用更大的步幅来替代之。此外,训练生成模型(例如VAE、GAN等)时通常为了达到更好的效果而舍弃池化层
归一化层
由于实践中没什么贡献,归一化层已经基本不太被人使用。详细内容参考Alex Krizhevsky的cuda-convnet library API
全连接层(FC)
与普通的前馈神经网络中的层无异
将全连接层转化为卷积层
这部分内容笔记暂时略去了
卷积神经网络体系结构
以上介绍了三种层:CONV、POOL和FC。此外,我们会把激活函数RELU也单独写作一层,该层对输入的每个值做一个非线性变换。下面讨论如何将这些部件组装起来,形成一个完整的卷积神经网络
层的模式
最常见的卷积神经网络体系结构是将若干个CONV-RELU层堆叠起来, 后面跟一个POOL层,然后将这种模式重复若干遍,直到图像的大小被合并到足够小为止。然后,通过若干个FC层,最后得到输出,例如每个类别的得分。也就是说,最常见的卷积神经网络体系结构满足如下模式
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC
这里*表示重复,POOL?表示有一个可选的池化层。通常情况下有
- \(N \ge 0\)(且通常\(N \le 3\))
- \(M \ge 0\)
- \(K \ge 0\)(且通常\(K < 3\))
通常将若干使用小尺寸滤波器的CONV堆叠在一起,而不是使用一个大感受野的CONV。假设堆起3个\(3 \times 3\)的CONV(层与层之间做一个非线性变换),这样,第一个CONV的神经元关注原始输入中\(3 \times 3\)的数据,第二个CONV的神经元关注第一层中\(3 \times 3\)的数据,相当于关注原始输入中\(5 \times 5\)的数据。那么,第三个CONV的神经元以此类推是关注原始输入中\(7 \times 7\)的数据。那么为什么不直接使用一个感受野为\(7 \times 7\)的CONV层呢?这样做有以下几个缺点
- 这样神经元计算的是输入的线性函数,而分三个CONV可以做两次非线性变换
- 假设所有输入有\(C\)个信道,感受野大小为\(7 \times 7\)的CONV层有\(C \times (7 \times 7 \times C) = 49C^2\)个参数,而堆叠的CONV层有\(3 \times (C \times (3 \times 3 \times C))\)个参数,参数数量更少,而且可以表示输入中更强力的特征
堆叠小感受野CONV的唯一缺点是,在做反向传播时,需要更多内存来存储中间CONV的结果
需要注意的是,从Google的Inception架构开始,CNN的联通结构变得更加复杂
层的大小
输入层的大小通常应该能被2整除很多次,常见的设置如32、64、96、224、384、512
卷积层通常使用小的滤波器(\(3 \times 3\)或最多\(5 \times 5\)),使用步幅\(S=1\)。当补零数\(P=(F-1)/2\)时,卷积层会保留原始输入大小。一般不使用更大的滤波器,即便要如此做,也把它放在第一个卷积层,直接接受原始输入。一般来讲,小的步幅(\(S=1\))在实践中效果更好,而且可以把所有空间降采样的任务都交给池化层,让卷积层专注于转换输入。补零也可以改善模型效果,因为如果不补零,输入的尺寸在每个卷积层处理后都会变小,图片边界上的信息消失太快
池化层用来对输入的空间维度降采样,通常使用\(F=2\)的最大池化层,步幅\(S=2\)。另一种做法是设\(F=3\)。一般情况下不要把池化层的感受野大小设成大于3的数,因为这样会损失太多信息,效果不好
如果网络难以拟合,一种比较好的办法是降低batch大小。CONV比较吃显存,要注意
成熟的体系结构
包括了LeNet、AlexNet、ZFNet、GoogLeNet、VGGNet和ResNet
