无Hessian矩阵(Hessian-Free, HF)优化法及其应用
HF优化原理
假设损失函数是一个二次曲线(曲率恒定),确切说,是一个碗口向上的抛物线,那么在这个曲线上选定方向,向前一直前进,误差在重新变大之前会减少多少?这个值取决于梯度和曲率的比值,所以如果选定的方向是好的方向,这个比值应该高。也就是说,梯度小的地方曲率也小
之前在讲神经网络优化的时候,曾经提到过,如果选最陡的方向做梯度下降,那么有可能这个方向并没有指向我们真正想去的方向。不过,如果误差表面的横截面是一个正圆形,那么梯度的方向就可以用了。牛顿法的思路就是使用一个线性变换将椭圆形的横截面转变成圆形,即将梯度乘以曲率矩阵(Hessian矩阵)的逆: \[ \Delta {\bf w} = -\epsilon {\bf H}({\bf w})^{-1}\frac{dE}{d\bf w} \] 如果损失函数的纵截面是二次曲线,\(\epsilon\)选择合适,使用牛顿法可以直达靶心!但是这里的问题是,如果权重特别多,达到百万量级,那么Hessian矩阵里面会有万亿个项。因为曲率矩阵里的每一个元素指明的是,当我们沿着某方向移动时,梯度在任一方向的变化量,即 \[ {\bf H} = \left[\begin{matrix}\frac{\partial^2E}{\partial w_1^2} & \frac{\partial^2E}{\partial w_1\partial w_2} & \cdots & \frac{\partial^2E}{\partial w_1\partial w_n} \\ \frac{\partial^2E}{\partial w_2\partial w_1} & \frac{\partial^2E}{\partial w_2^2} & \cdots & \frac{\partial^2E}{\partial w_2\partial w_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2E}{\partial w_n\partial w_1} & \frac{\partial^2E}{\partial w_n\partial w_2} & \cdots & \frac{\partial^2E}{\partial w_n^2}\end{matrix}\right] \] 如果损失函数的横截面是正圆,那么Hessian矩阵中非对角线元素都是0,即沿着该方向移动时,梯度在其它方向上不会变化,因此梯度方向就是真正想去的方向。但是如果损失函数的横截面是椭圆,Hessian矩阵中非对角线元素就不是0,沿着该方向变化来修改权重的某个分量,梯度在其它方向上的分量也会改变。因此如果同时修改所有权重,那么其它权重的变化会导致梯度在权重的第一个分量上的变化,使得事情可能会变得更糟(其它权重的变化导致梯度的第一分量符号被逆转,走向相反方向)。权重维度越大,就应该越小心
由于大的神经网络中Hessian矩阵的项太多,很难求逆,因此需要解决这个问题。LeCun组提出的一个方案是只关注对角线上的前若干个元素,但是这些元素太少了,如果这么做基本上要忽略掉矩阵中其它所有元素。另一种做法是使用各种方法近似Hessian矩阵,降低它的秩,例如HF法、LBFGS法等等。在HF法中,我们对Hessian矩阵做一个近似,然后假设这个近似是对的,使用共轭梯度法(conjugate gradient)来减小误差,接着再做一次近似和优化,如此往复。如果在RNN中使用这种方法,一般要加一个正则化,防止优化方法将隐藏层状态改变太多(因为RNN一般是按时间展开,如果较早时间步中的隐藏状态发生了巨大变化,会连锁影响后面所有的隐藏状态。因此一般可以加状态改变量的平方作为正则项)
共轭梯度法的核心思想是,先找到某个方向的最小值,一直前进,然后再找新的方向。寻找新的方向时,保证新的方向与前一个方向“共轭”,这样就不会破坏已经取得的前面所有方向的梯度。假设这个二次曲面是在\(N\)维空间上的二次曲面,共轭梯度法保证在\(N\)步之后可以找到最小点,因为它的原理就是每一步都在一个独立的(尽管不是正交的)方向达到该方向上梯度为0的点。一个更好的性质是,在远小于\(N\)步之后,算法就能非常接近最小值点。此外,共轭梯度在非二次曲面上效果也不错,也适用于mini batch的学习
HF优化器的原理就是,先使用一个二次表面逼近原始表面,然后再在这个近似的二次表面上使用共轭梯度法
使用HF的字符模型
字符模型
通常情况下,讲到神经网络语言模型,提到的都是单词级别的语言模型,也就是把一句话看作是由单词组成的字符串。但是,就把这些句子看成是由字母组成的字符串也是有好处的。假设现在想通过“阅读”维基百科的所有文章来构建一个模型,如果需要将wiki里的所有文本都预处理成单词,那么就会比较麻烦,包括以下几个方面
- 词素(morpheme)。词素是表达词意的最小单位,但是具体一个单词里哪些部分可以算作是词素,这个是见仁见智的
- sub-word。有的时候,词的一部分可能反映了某种意思。例如,英语里以sn-开头的词都多少与嘴唇和鼻子有关,例如sneeze, snarl等等。这里是否包含了一些规律?
- 例如New York这样的词,大多数情况下是希望把它看做是一个词,但是有的时候,例如谈论New York minster roof的时候,应该把它看作是两个词
- 最后,对于黏着语,这类语言的单词通常都附着了多个语法成分,因此可以做出来特别长的单词。例如芬兰语的ymmärtämättömyydelläänsäkään对应了英语的“even with his/her/their lack of understanding”。这个词在字典里没有,而且日常生活中也很少用到
因此设计一个RNN来建立一个字符模型是有必要的,即使用\(T\)时刻的隐藏状态和输入来决定\(T+1\)时刻的隐藏状态,然后通过一个softmax来产生下一个可能的字符。假设输入字符表有86个, 隐藏层有一层,里面有1500个隐藏单元,那么下面给出了这个RNN的示意图
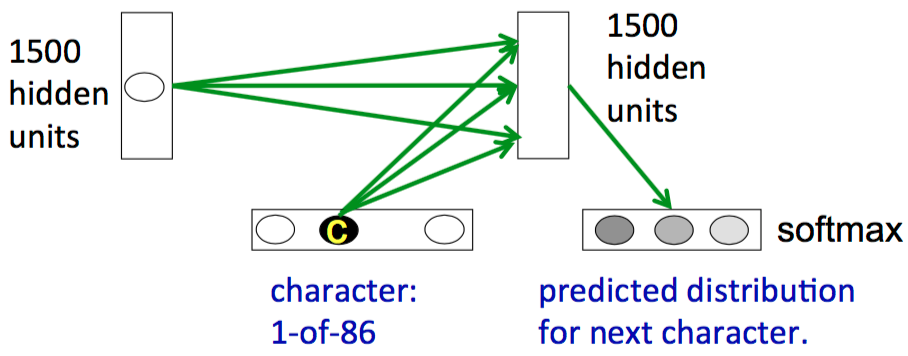
但是一般并不会使用这种体系结构(这里存疑,因为感觉现在常见的用的的确是这种结构)。为什么呢?由于理论上任何前缀后面都可以跟86个字母中的任意一个,因此最后可以组成一个很大的树,如图所示。每当接受一个字符输入时,都会沿着这棵树向下走向一个新的节点。对于长度为\(N\)的词,如果用的是统计的方法,那么就需要存储整个的这棵大树,每条边实际上存储了给定前面所有前缀的情况下,接下来的字母的概率。在RNN里,这样的前缀信息被隐藏状态向量来表示,也就是说,每个输入都会把当前的隐藏状态转化为一个新的隐藏状态
使用神经网络的隐层(隐式地)实现这棵树有一个好处,就是可以共享很多结构。例如当前面的输入为f, i, x时,已经可以判断出来正在输入的可能是一个动词,而这时如果再输入i,后面跟着的很可能会是n和g。这种“前面是动词,输入i,后面可能是ng”的知识可以共享给所有其他动词。需要再着重提一下的是,是当前的隐藏状态和当前的输入共同决定了接下里的输出。如果隐藏状态里没有动词信息,那么输入i并不一定期望后面是ng。
乘性连接(multiplicative connection)
基于前面的介绍,现在要解决的问题是,如何使用当前的输入字符来确定从当前隐藏状态到下一个隐藏状态的权重矩阵。对于原始的做法,实际上要把所有86个字符都试一遍,来找出一个1500 x 1500的矩阵,这样会有很多参数(86 x 1500 x 1500),容易过拟合。如果非要使用这种方法,也需要数据量很大的时候才行(但是我个人感觉这个条件已经可以很容易地满足了)
前面提到,对不同的单词,可以有一些通用的“特征”。那么一个思路就是,使用这样的特征来减少参数的数量,同时仍然实现这种“乘性连接”的功能。即,对着86个字符训练不同的转移矩阵,但是让这些矩阵共享参数。在这里,引入“因子”(factor)的概念,并假设因子的输入是两个组a和b,输出是一个组c。如下所示
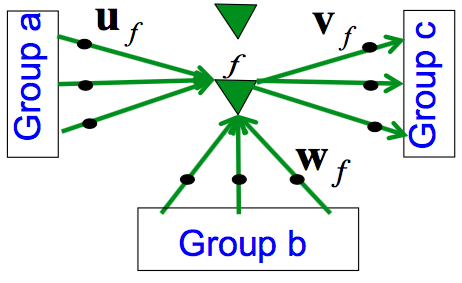
因子会先对其两个输入组各自计算加权和\({\bf a}^\mathsf{T}{\bf u}_f\)以及\({\bf b}^\mathsf{T}{\bf w}_f\),然后,将这两个积再相乘,可以得到一个标量。用这个标量去缩放输出权重\({\bf v}_f\)可以得到组c的输入,即 \[ {\bf c}_f = ({\bf b}^\mathsf{T}{\bf w}_f)({\bf a}^\mathsf{T}{\bf u}_f){\bf v}_f \] 沿用之前的例子,这时,因子从上一个隐藏状态接收到1500个参数,从字母表接收到86个参数,产生给下一个隐藏状态1500个参数,这样,因子总共只需要3086个参数
这个过程也可以换一个角度理解,即每个因子实际上定义了一个非常简单的转换矩阵,其秩为1。上面的等式等价于下式 \[ {\bf c}_f = ({\bf b}^\mathsf{T}{\bf w}_f)({\bf u}_f{\bf v}_f^\mathsf{T}){\bf a} \] 这里外积\({\bf u}_f{\bf v}_f^\mathsf{T}\)就是秩为1的矩阵
最后,将所有因子的\({\bf c}_f\)加起来,就得到了送入c的转换矩阵 \[ {\bf c} = \left(\sum_f ({\bf b}^\mathsf{T}{\bf w}_f)({\bf u}_f{\bf v}_f^\mathsf{T})\right){\bf a} \] 也就是说,每个因子都给出了一个秩为1的矩阵,而字母表\({\bf b}\)中的每个字母决定了这些矩阵的权重
使用HF优化器预测下一个字符
Ilya Sutskever从英文维基挑出了500万个长度为100个字符的句子,从第11个字符开始预测。训练在一块GPU上持续进行了大约一个月,最后得到的模型效果还不错,可能是到2012年为止效果最好的单神经网络模型(除非将多个模型组合起来才能击败他)。这个模型的一个显著特点是,可以匹配长距离的括号和引号
具体生成字符串的做法是,以默认的隐藏状态开始,给出一个句子。模型随着读入这个句子的字符时会更新隐藏状态。读完这个句子以后,开始预测接下来的字符。对于接下来的字符,模型会产生一个概率分布,然后我们随机从这个分布中取一个字符,告诉它这个字符就是我们要的,让它接着预测(也就是说默认它预测的字符总是对的),直到我们想结束这个过程为止
观察这个模型产生的文本,可以发现有这么一些特点:
- 尽管有的词搭配很怪,例如Opus Paul at Rome,但是考虑到Opus, Paul和Rome之间存在关系,还是可以理解的
- 不会产生特别长的句法结构,每一个句号后面新的句子都会开始一个新的主题
- 很少产生英语单词表里没有的词。即便是产生了,这个词也很像英语单词,例如ephemerable
- 尽管有时候会产生不匹配的括号,但是它也会匹配长距离的括号和引号
另一个有趣的实验是,给一个自造词,看看会有什么结果。Hinton选择了thrunge这个词,它不存在于词典里,但是看着像是一个动词。如果前面给的是Sheila,那么对于Sheila thrunge模型会预测接下来的字母是s,这意味着它能发现主语是单数,前面有点像动词。如果前面给People,那么对于People thrunge模型预测接下来的字符是空格,说明它能掌握people是复数这个特征。如果前面给Shiela, 并将t大写,那么对于"Shiela, Thrunge"它会补成"Shiela, Thrungelini del Rey",即一个人名——而且这个人名还不错
经过实验观察,可以肯定的是,模型能够学到以下知识
- 能够知道什么是词,长什么样。它产生的词绝大部分都是英语单词,而且知道句首字母大写,产生出的日期格式也没什么问题。即便是产生了虚构的,非英语的单词,也很难看出来。它可以产生专有名词,也知道日期和数字应该出现的语境
- 能够产生匹配的括号和引号,而且某种意义上还会对括号和引号记数。例如,如果给出的字符没有括号/引号,它后面基本不会给出右括号/引号。如果给出的字符有左括号/引号,那么在20个字符以内基本就会生成对应的符号
- 能够掌握某些语法规则,不过很难说具体的语法规则是什么,看上去像是很多比较弱的句法关联。例如,在产生“柏拉图”这个词以后不久,就会产生“维特根斯坦”。模型大概知道卷心菜和蔬菜之间存在关系,但是并不知道具体是什么关系。当然,这种特点是可以理解的,人类也会存在。假设现在玩一个游戏,提问者问完问题以后回答者必须马上喊出答案,那么在听到问题“奶牛喝什么”以后大部分人的意识都是喊出“牛奶”。实际上奶牛是不喝牛奶的,但是人们听到“奶牛”和“喝”以后都会想到牛奶,即便逻辑上不通
Mikolov组使用了类似的技术来预测下一个单词会是什么单词。总体而言,RNN不需要太多数据就能达到其他模型能够达到的效果,而且随着数据集的增大,RNN的效果提升得更快
回声状态网络
回声状态网络(Echo State Network, ESN)使用一种更聪明的技巧来让学习RNN变得更容易。它把网络中的链接初始化为一个大的,耦合的振子(oscillator)库,并将输入转化为这些振子的状态,通过这些状态来预测输出。ESN学到的唯一东西是如何将振子与输出相关联,而不用学习隐藏层之间,以及隐藏层与输出层之间的链接。不过,ESN需要大量的隐藏状态
更具体地说,ESN随机初始化所有的隐藏状态并将其固定,然后训练这些隐藏状态如何去影响输出。这种做法与感知机的思路有点像,它最后训练的就是从大量随机隐藏状态到输出的线性模型。此外,这种方法与支持向量机SVM也有异曲同工之妙。但是,这些随机的权重必须设置得非常精妙,才会避免出现梯度消失/梯度爆炸的现象。做法是保证隐藏层到隐藏层的权重满足如下性质:在每个迭代之后,活动向量的长度保持不变。即对于某个线性系统而言,其矩阵的谱半径(spectral radius)为1,也就是隐藏层到隐藏层的权重矩阵的最大特征值为1。在非线性系统中,如果权重被设置在一个合适范围之内,则输入能够在循环状态中回响很久
另一种重要的做法是使用稀疏连通性,即对隐藏层到隐藏层的权重矩阵,不去设置大量中等大小的权重,而是只保留少数几个很大的权重,其它的权重都设为0。这样,可以得到很多松耦合的振子,使得信息可以在网络的一部分中停留一段时间,不会很快被传播到其它部分。对于这种方法,需要小心选择输入层到隐藏层的连接数,要既保证能够得到松耦合的振子,还不会清除掉振子中包含的关于最近历史的信息
(中间的实验略)
ESN的好处是训练起来很快,因为只需要拟合一个线性模型,而且对一维时间序列的建模能力非常好,可以预测未来很长一段时间的数据。但是它不适合对高维数据建模(例如声音帧、视频帧等)。为了建模这样的数据,它需要的隐藏层单元数比RNN所需要的多很多。最近(2012年),Ilya Sutskever发现,使用ESN用到的初始化方法来初始化RNN,并使用带有动量的rmsprop优化方法,能很有效地训练RNN
