径向基函数网络假设函数
前面讲使用高斯核的SVM时曾经提到过这种模型的一个性质:在高斯核的帮助下,这种模型可以在无限维的空间里学习到一个最大间隔超平面。该模型的定义如下 \[ g_{\rm SVM}({\bf x}) = {\rm sign}\left(\sum_{\rm SV}\alpha_n y_n \exp(-\gamma\|{\bf x}-{\bf x}_n\|^2)+b\right) \] 从最后得到的假设函数来看,它做的事情还可以表述为,使用一系列高斯核函数做线性组合,它们各自的中心就是在支持向量上。高斯核函数又称为径向基函数(Radial Basis Function,RBF),这个词可以做如下分解:
- “径向”表示要求的函数值与某个距离有关,这个距离是新的点\(\bf x\)和已知点\({\bf x}_n\)之间的距离
- “基函数”表示这些函数要用来做线性组合。对于上式,系数就是\(\alpha_n y_n\)
如果定义\(g_n({\bf x}) = y_n\exp(-\gamma\|{\bf x} - {\bf x}_n\|^2)\),这个函数就表示新的点与已知点够不够近,越近给的票越多,这个票数就是\(y_n\)。这样一来,上面的SVM可以表示为 \[ g_{\rm SVM}({\bf x}) = {\rm sign}\left(\sum_{\rm SV} \alpha_n g_n({\bf x}) + b\right) \] 这样更清楚地表明\(g_{\rm SVM}\)其实就是\(g_n\)的线性组合,每个\(g_n\)代表一个径向假设。而径向基函数网络(RBF网络)就是这种模型的延伸。之所以说它是一个“网络”,就是因为其结构与之前讲过的神经网络有类似的地方。下图给出了两者的对比
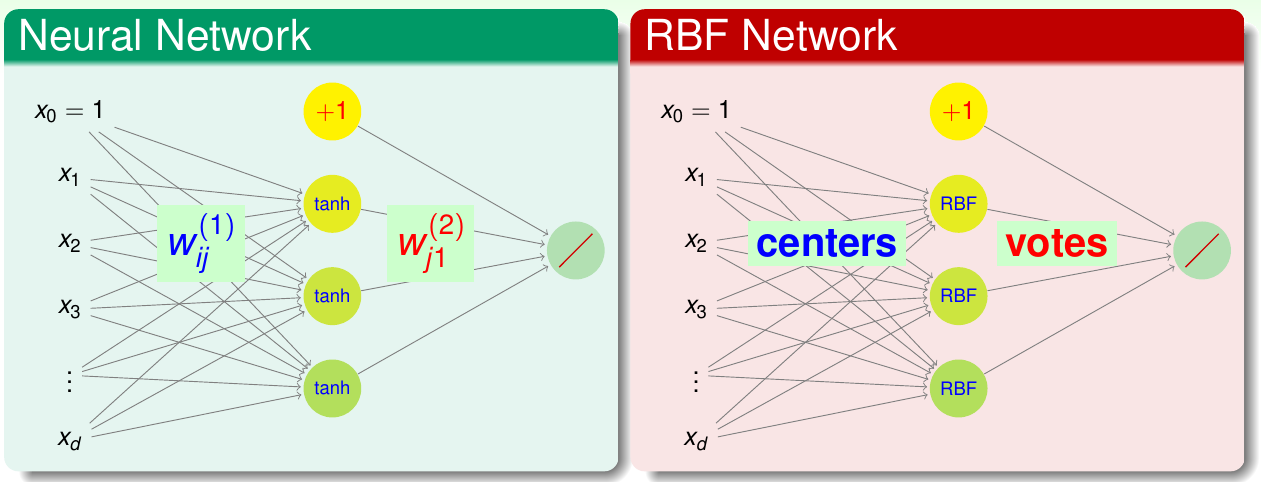
可以看出,两者的输出相同,都是线性组合。不同的地方在隐含层:神经网络是计算权重和输入的内积,然后做非线性变换\(\tanh\);而RBF网络则是计算两点之间的距离,然后使用高斯函数做变换。从历史上讲,RBF网络实际是神经网络的分枝
总体来看,RBF网络的假设函数可以写成如下形式 \[ h({\bf x}) = {\rm Output}\left(\sum_{m=1}^M \beta_m {\rm RBF}({\bf x}, \boldsymbol{\mu}_m)+b\right) \] 其包括以下几个部分:
- 径向基函数\(\rm RBF\),注意高斯函数只是其中一种,可以有其它选择
- 中心点\(\boldsymbol{\mu}_m\)
- 投票\(\beta_m\)
- 输出转换\(\rm Output\)
其中\(\boldsymbol{\mu}_m\)和\(\beta_m\)是两个关键变量
如果把高斯核SVM看作是RBF网络的一个特例,则存在以下对应关系:
- \({\rm RBF}\):高斯函数
- \(\rm Output\):\(\rm sign\)函数
- \(M\):支持向量的数量
- \({\boldsymbol{\mu}_m}\):SVM的各个支持向量
- \(\beta_m\):由对偶问题解出的\(\alpha_m y_m\)
因此RBF网络的问题就是,对给定的\(\rm RBF\)和\(\rm Output\) ,求出\(\boldsymbol{\mu}_m\)和\(\beta_m\)
前面提到过,核函数是在变换后的空间\(\mathcal{Z}\)中的内积,因此能保证满足Mercer定理即可。核函数实际上描述了向量之间的相似性,而RBF描述的也是相似性,只不过这种相似性可以直接通过向量之间的距离来计算,因此可以定义不同的RBF,只要能满足对距离的定义就可以。一般情况下,随着距离的变大,RBF的值应该单调不增。也就是说,核函数和RBF是两种对距离的定义,而高斯函数就属于这两者的交集之中。除此以外,神经网络中每个神经元也可以看作是描述了一种距离的计算方式,为\(\tanh(\gamma {\bf x}^\mathsf{T}{\bf x}' + 1)\)。在DNA序列的应用中,可以使用编辑距离
总而言之,RBF说明相似性是一种很好的定义特征变换的方法,这种相似性通过计算点到中心的距离可以获得
径向基函数网络学习
前面讲过,RBF网络的目的是找到一些中心,以及将RBF值线性组合起来的系数。在最简单的例子中,可以把看到过的所有数据点都当做中心。这种RBF网络称为全RBF网络,满足\(M=N\)以及每个\(\boldsymbol{\mu}_m = {\bf x}_m\)。其物理意义可以解释为,训练集中的每条数据\({\bf x}_m\)对其周围的数据都应该有一定的影响,而影响力由\(\beta_m\)决定。例如,假设每个点的影响力都一样,则对于新点,训练集中的每个点都会根据其到新点距离的远近做投票:总体来讲,一人一票,但是离得越近,系数越大。即\(\beta_m = 1 \cdot y_m\)。这种假设函数的形式为 \[ g_{\rm uniform}({\bf x}) = {\rm sign}\left(\sum_{m=1}^N y_m\exp(-\gamma \|{\bf x}-{\bf x}_m\|^2)\right) \] 即训练集中的每条数据都可以对新数据的所属类别发表意见,模型将所有人的意见收集起来,根据相似性分配票数,加权求和,最后输出。显然,对离新点\(\bf x\)最近的数据点,它与新点的高斯函数值最大,说话最有分量。由于高斯函数随距离增大衰减很快,因此实际上往往这个点的标签可以决定最后结果。从这个角度来说,可以避免求和项,只需要找到距离新点最近的那个点就可以了。此时,模型的聚合退化成了模型的选择,假设函数变为 \[ g_{\rm nbor}({\bf x}) = y_m {\rm\ such\ that\ }{\bf x}{\rm\ closest\ to\ }{\bf x}_m \] 这种方法称为最近邻法。在这种算法的基础上可以做一些扩展:不只找最近的邻居,而是找\(k\)个最近的邻居,将它们的结果做聚合。这种扩展的方法称为\(k\)-最近邻法(kNN)。kNN是一种比较“懒”的算法,但是却非常符合直觉。不过这种算法在测试时会比较费事
全RBF有什么好处呢?考虑将这种网络用在回归问题中,误差函数使用平方误差,而且不再指定\(\beta_m\),而是让算法去优化这些系数。那么模型其实就是对经RBF变换过的数据求解线性回归。变换后的数据为 \[ {\bf z}_n = [{\rm RBF}({\bf x}_n, {\bf x}_1), {\rm RBF}({\bf x}_n, {\bf x}_2), \ldots, {\rm RBF}({\bf x}_n, {\bf x}_N)] \in \mathbb{R}^N \] 由前面的结论,可以轻易求出最优的系数\(\boldsymbol{\beta} = {\rm (Z^\mathsf{T}Z)^{-1}Z^\mathsf{T}}{\bf y}\),其中\(\rm Z\)是对称方阵。进一步地,如果使用高斯函数做RBF,且所有\({\bf x}_n\)都不同,则这个\(Z\)还是可逆的,系数\(\boldsymbol{\beta}\)可以继续化简为\(\boldsymbol{\beta} = {\rm Z}^{-1}{\bf y}\)
得到这个结果以后,如果要用得到的\(g\)送入原来的训练数据,有 \[ g_{\rm RBF}({\bf x}_1) = \boldsymbol{\beta}^\mathsf{T}{\bf z}_1 = {\bf y}^\mathsf{T}{\rm Z^{-1}}({\rm Z}的第一列) = {\bf y}^\mathsf{T} \left[\begin{array}{c}1 & 0 & \ldots & 0\end{array}\right]^\mathsf{T} = y_1 \] 以此类推,\(g_{\rm RBF}({\bf x}_n) = y_n\),\(E_{\rm in}(g_{\rm RBF}) = 0\),意味着有过拟合的危险。如果使用岭回归,则\(\boldsymbol{\beta} = ({\rm Z^\mathsf{T}Z} + \lambda{\rm I})^{-1}{\rm Z^\mathsf{T}}{\bf y}\)就不会产生前面这种“完美”的结果。考虑到\(\rm Z\)是两个点的高斯函数值,也就是使用高斯核得到的核矩阵\(\rm K\),则这个模型跟前面讲过的核岭回归有异曲同工之妙。在核岭回归中,\(\boldsymbol{\beta}_{\rm kernel\_ridge\_regression} = ({\rm K} + \lambda{\rm I})^{-1}{\bf y}\)。只不过核岭回归是在无限多维空间中做正则,而正则化的全RBF是在\(N\)维空间中做正则
另外,回顾前面SVM的做法,它其实没有用到所有数据点做中心点,因此可以将中心点数量减少使得\(M <\!\!< N\),也可以起到正则化的作用。从物理意义上看,相当于不再让每个点都有话语权,而是选择一些代表出来去投票,代表所有人的意见。那么接下来的问题就是,如何找到好的代表呢?
K均值聚类算法
要寻找好的代表,首先可以看一个比较简单的情况。假设在训练集里,有\({\bf x}_1 \approx {\bf x}_2\),那么它俩的RBF值应该也接近,所以没有必要在RBF网络里保存两份近似的值\({\rm RBF}({\bf x}, {\bf x}_1)\)和\(\rm{RBF}({\bf x}, {\bf x}_2)\),而是让这两个数据点共用一个代表,也就是把这两个点聚类起来,得到\(\boldsymbol{\mu} \approx {\bf x}_1 \approx {\bf x}_2\)
在本系列课程最开始的时候就提到过聚类问题,这是一种非常典型的非监督学习问题。稍微形式化地说,它是要把数据集合\(\{ {\bf x}_n\}\)划分为\(M\)个不相交的集合\(S_1, S_2, \ldots, S_M\),而且为每个\(S_m\)选择一个代表\(\boldsymbol{\mu}_m\),使得对任意\({\bf x}_n \in S_m \Leftrightarrow \boldsymbol{\mu}_m \approx {\bf x}_n\)。因此,聚类问题通常使用的误差函数通常是看数据点到自己所属类别的代表的距离的平方总和,写作如下形式 \[ E_{\rm in}(S_1, \ldots, S_M; \boldsymbol{\mu}_1, \ldots, \boldsymbol{\mu}_M) = \frac{1}{N}\sum_{n=1}^N\sum_{m=1}^M [\![{\bf x}_n \in S_m]\!]\|{\bf x}_n - \boldsymbol{\mu}_m\|^2 \] 聚类算法就是要最小化这样的目标函数,即解决如下最优化问题 \[ \min_{\{S_1, \ldots, S_M; \boldsymbol{\mu}_1, \ldots, \boldsymbol{\mu}_M\}}\sum_{n=1}^N\sum_{m=1}^M [\![{\bf x}_n \in S_m]\!]\|{\bf x}_n - \boldsymbol{\mu}_m\|^2 \] 这并不是一个容易解决的问题,因为它是一种组合最优化问题,而且变量\(S_1, \ldots, S_M\)都是类型变量,\(\boldsymbol{\mu}_1, \ldots, \boldsymbol{\mu}_M\)却是数值变量。不过因为这些变量可以分成两类\(S\)和\(\boldsymbol{\mu}\),可以尝试使用各个击破的方法,先固定一组变量,对另一组变量做最优化,然后再反过来
首先,固定\(\boldsymbol{\mu}_1, \ldots, \boldsymbol{\mu}_M\),为每个\({\bf x}_n\)挑选一个最好的\(S_m\)。由于每个\({\bf x}_n\)都必须且只能对应一个最好的\(S_m\),而\(\boldsymbol{\mu}_m\)固定所以可以知道\({\bf x}_n\)到每个\(\boldsymbol{\mu}_m\)的距离,因此这个最优化动作很简单,只需要把离\({\bf x}_n\)最近的那个\(\boldsymbol{\mu}_m\)分给它就好了
接下来,固定\(S_1, \ldots, S_M\),选出各个类(簇)的代表。此时原始最优化问题退化成一个与\(\boldsymbol{\mu}_m\)有关的无限值最优化问题,因此只需要求目标函数的梯度然后令其等于0即可。有 \[ \nabla_{\boldsymbol{\mu}_m}E_{\rm in} = -2\sum_{n=1}^N[\![{\bf x}_n \in S_m]\!]({\bf x}_n - \boldsymbol{\mu}_m) = -2\left(\left(\sum_{ {\bf x}_n \in S_m} {\bf x}_n\right)-|S_m|\boldsymbol{\mu}_m\right) \] 令上式为0,则\(\boldsymbol{\mu}_m\)是属于\(S_m\)的\({\bf x}_n\)的均值
上述过程其实就是非常有名的聚类算法——K均值聚类算法的核心过程(这里的K其实就是前面说的M)。其完整流程如下:
- 初始化\(\boldsymbol{\mu}_1, \boldsymbol{\mu}_2, \ldots, \boldsymbol{\mu}_K\)。通常做法是在\({\bf x}_n\)里随机选\(K\)个点
- 交替最优化\(E_{\rm in}\),即重复以下过程直至收敛(收敛的判定方法通常是\(S_1, \ldots, S_K\)不再变化
- 最优化\(S_1, S_2, \ldots, S_K\),即把\({\bf x}_n\)分给离它最近的那个\(\boldsymbol{\mu}_i\)所属的类簇
- 最优化\(\boldsymbol{\mu}_1, \boldsymbol{\mu}_2, \ldots, \boldsymbol{\mu}_K\),即对每个\(S_k\),求属于该类簇所有点的均值
由于这个过程一直在使\(E_{\rm in}\)变小,因此算法一定会收敛
K均值聚类算法可能是所有聚类算法里最有名的一个,其核心思路就是做交互最优化
可以把K均值聚类算法与RBF网络结合起来,算法如下
使用K均值聚类算法(这里\(K=M\))得到\(M\)个中心点\(\{\boldsymbol{\mu}_m\}\)
使用RBF(例如高斯函数)围绕\(\boldsymbol{\mu}_m\)构建变换\(\boldsymbol{\Phi}({\bf x})\) \[ \boldsymbol{\Phi}({\bf x}) = [{\rm RBF}({\bf x}, \boldsymbol{\mu}_1), {\rm RBF}({\bf x}, \boldsymbol{\mu}_2), \ldots, {\rm RBF}({\bf x}, \boldsymbol{\mu}_M)] \]
在变换后的数据\(\{(\boldsymbol{\Phi}({\bf x}_n), y_n)\}\)上运行线性模型,得到\(\boldsymbol{\beta}\)
返回\(g_{\rm RBFNET}({\bf x}) = {\rm LinearHypothesis}(\boldsymbol{\beta}, \boldsymbol{\Phi}({\bf x}))\)
就像自动编码器一样,这里RBF网络也是使用无监督学习算法来萃取特征
K均值聚类和径向基函数网络实战
实验说明K均值聚类算法的效果对K的设置和初始点的设置比较敏感。以及全RBF网络和kNN由于需要遍历所有数据集,因此预测时效率不高,所以不是很常用
