线性网络假设函数
在本系列课程的第一讲里,曾讲到过一种称为“推荐系统”的问题,也就是根据用户对电影的评分历史,估计ta对一部新电影可能的评分。也就是说,对于第\(m\)部电影,其数据集\(\mathcal{D}_m\)可以表示为 \[ \{(\tilde{\bf x}_n = (n), y_n = r_{nm}): \ {\rm user\ }n{\rm\ rated\ movie\ }m\} \] 这种数据与前面介绍的数据最大的不同是,\(\tilde{\bf x}_n\)是抽象特征,只是一个用户的编号ID。我们不知道ta背后是男是女,是长是幼,对电影是什么口味,只知道ta打过了哪些分数。那么如何从这些数据里学到每个用户的喜好呢?
首先,要考虑如何表示这种特征。需要注意的是,用户ID只是一个离散的数值,没有什么实际意义。此外,对用户ID的比较、四则运算等也是没有意义的(一般来说,用户ID越小,说明用户注册时间越早,所以可能会透露出一些额外的信息。不过这里认为评分和注册时间没有什么关系)。类似的特征有很多,例如人的血型,编程语言种类等等。这种没有数值关联性的特征通常称为类别特征。目前为止,介绍过的大部分模型基本都是接受数值特征,例外情况只有决策树及其延伸(例如随机森林)。因此,要把这些类别特征利用到更广泛的模型中,就需要将它们转成数值特征,这也是特征变换的一种。不过这种特征变换通常是预先定义好的,这种预先定义的动作就称为编码。一种比较简单的编码方式称为二值向量编码方式(binary vector encoding,更常见的称呼方法是独热编码 one hot encoding):假设对于该变量有\(t\)种取值,那么就建立一个长度为\(t\)的数组,每一位都分给一种可能的取值情况。当该特征属于某种取值时,其对应的那一位置为1,其余位置为0。例如,人的血型有A、B、O和AB四种取值情况,那么这四个值可以分别表示为 \[ \begin{align*} {\tt A} &= [1, 0, 0, 0]^\mathsf{T} \\ {\tt B} & = [0, 1, 0, 0]^\mathsf{T} \\ {\tt O} &= [0, 0, 1, 0]^\mathsf{T} \\ {\tt AB} &=[0, 0, 0, 1]^\mathsf{T} \\ \end{align*} \] 因此,对第m个电影,编码后的数据\(\mathcal{D}_m\)可以表示为 \[ \{({\bf x}_n = {\rm OneHotEncoded}(n), y_n = r_{nm}): \ {\rm user\ }n{\rm\ rated\ movie\ }m\} \] 进一步地,可以把用户对所有电影的评分收集起来,得到一个联合数据\(\mathcal{D}\) \[ \{({\bf x}_n = {\rm OneHotEncoded}(n), {\bf y}_n = [\begin{array}{cccccc}r_{n1} & ? &? &r_{n4} & r_{n5} & \ldots & r_{nM}\end{array}]^\mathsf{T})\} \] 由于用户基本不可能对所有电影都作出过评分,因此可以将用户没有评过分的项用“?”标记起来
这个特征仍然抽象,还是需要考虑怎么做进一步的特征提取和变换。由于前面讲到的神经网络有这方面的功能,因此可以用神经网络来解决这个问题。假设网络使用如下结构构建:输入对应使用者,是一个\(N\)维独热编码过的向量,中间使用\(\tilde{d}\)个神经元做隐藏层,最后输出是一个\(M\)维的向量对应电影评分,那么这个网络很像前面的自动编码器,看上去应该是有提取特征的功能。注意为了简单起见,网络里不带常数项\({\bf x}_0^{(\ell)}\)。此外,这个应用里隐藏层不需要做非线性变换\(\tanh\),因为输入向量太稀疏了。综合起来,网络的结构可以用下图表示。由于隐藏层都使用的是线性变换,因此该网络也可以称为线性网络
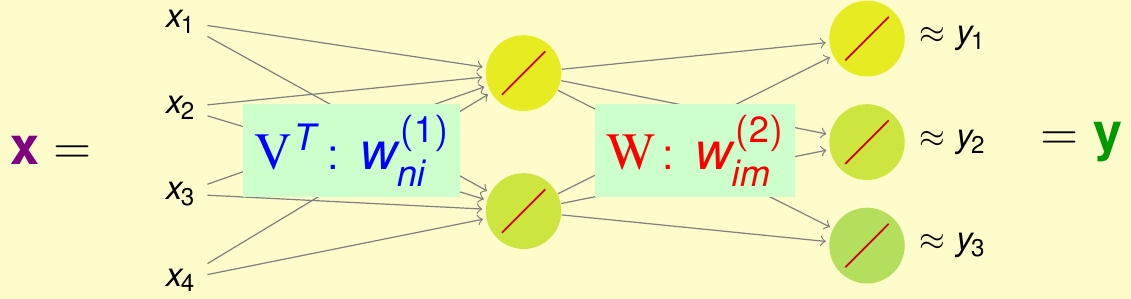
按照上图所示,将两层权重分别矩阵化 \[ \begin{align*} {\rm V}^\mathsf{T} &= [w_{ni}^{(1)}] \in \mathbb{R}^{N \times \tilde{d}} \\ {\rm W} &= [w_{im}^{(2)}] \in \mathbb{R}^{\tilde{d} \times M} \end{align*} \] 则线性网络的假设函数可以写为 \[ h({\bf x}) = {\rm W^\mathsf{T}V}{\bf x} \] 其中每个用户\(n\)的输出为\(h({\bf x}_n) = {\rm W}^\mathsf{T}{\bf v}_n\),这里利用了稀疏向量的性质,\({\bf v}_n\)是\(\rm V\)的第\(n\)列
这样,用于推荐系统的线性网络,就是要最优化\(\rm V\)和\(\rm W\)
基本矩阵分解
前面给出的假设函数中,\({\rm V}{\bf x}\)这一项可以看作是对\({\bf x}\)做的特征变换\(\boldsymbol{\Phi}({\bf x})\)。这样,如果单独看第\(m\)个电影,其对应的实际上就是一个线性模型\(h_m({\bf x}) = {\bf w}_{m}^\mathsf{T}\boldsymbol{\Phi}({\bf x})\),训练的目标就是希望这个模型对每个\(\mathcal{D}_m\)都能达到\({\bf w}_m^{\mathsf T}{\bf v}_n \approx y_n = r_{nm}\)的效果。因此,可以使用平方误差来做损失函数,即 \[ E_{\rm in}(\{ {\bf w}_m\}, \{ {\bf v}_n\}) = \frac{1}{\sum_{m=1}^M |\mathcal{D}_m|} \sum_{ {\rm user\ }n{\rm\ rated\ movie\ }m}(r_{nm} - {\bf w}_m^{\mathsf T}{\bf v}_n)^2 \] 由于内积的对称性,有\(r_{nm} \approx {\bf w}_m^{\mathsf T}{\bf v}_n = {\bf v}_n^\mathsf{T}{\bf w}_m\)。将这个式子矩阵化,有\(\rm R\approx V^\mathsf{T}W\),其中\(\rm R\)是评分矩阵,\(\rm V\)是所有用户特征组成的矩阵,\(\rm W\)是所有电影特征(权重)组成的矩阵。如果能通过已知的一部分\(\rm R\)(不需要知道所有的元素)将其分解为\(\rm V\)和\(\rm W\)的乘积,那么就能得到使用者特征,和每部电影应该怎么做线性组合。也就是说,在这个模型里做的模型是由已知评分反推那些特征影响用户评分,以及每部电影有哪些元素。例如,某个维度可能对应用户是否喜欢喜剧片,以及电影是否是喜剧片,如下图所示
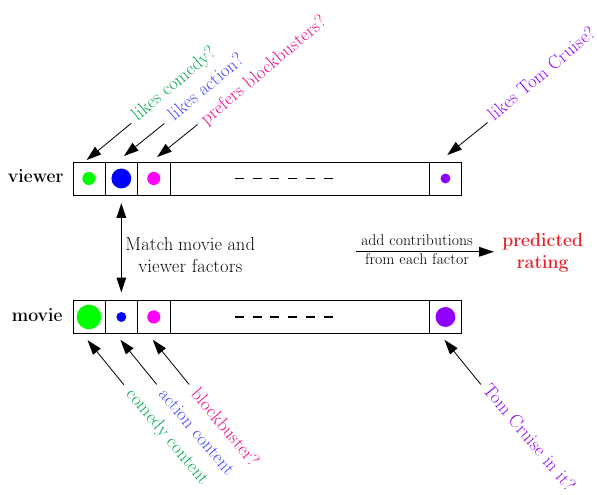
矩阵分解经常用来从抽象特征中提取具体特征
矩阵分解的最优化问题可以进一步推演 \[ \begin{align*} \min_{\rm W, V}E_{\rm in}(\{ {\bf w}_m\}, \{ {\bf v}_n\}) &\propto \sum_{ {\rm user\ }n{\rm\ rated\ movie\ }m}(r_{nm} - {\bf w}_m^{\mathsf T}{\bf v}_n)^2 \\ &= \sum_{m=1}^M \left(\sum_{( {\bf x}_n, r_{nm}) \in \mathcal{D}_m} (r_{nm} - {\bf w}_m^{\mathsf T}{\bf v}_n)^2 \right) \end{align*} \] 这里可以看到又出现了两组变量,难以同时优化,但是可以交替优化:先固定\({\bf v}_n\),最小化\({\bf w}_m\),此时就是求解一组线性回归模型,不过不带常数项;然后,固定\({\bf w}_m\),最小化\({\bf v}_n\),也是求解一组线性回归模型,只是此时是求解关于用户的线性回归模型,而且也不带常数项。这种算法称为交替最小二乘法。其完整表述如下
- 随机初始化\(\tilde{d}\)维向量\(\{ {\bf w}_m\}, \{ {\bf v}_n\}\)
- 交替最小化\(E_{\rm in}\):重复如下过程直到收敛
- 最优化\({\bf w}_1, {\bf w}_2 ,\ldots, {\bf w}_M\),对第\(m\)个电影,对数据集\(\{({\bf v}_n, r_{nm})\}\)求解一个线性回归模型,更新\({\bf w}_m\)
- 最优化\({\bf v}_1, {\bf v}_2 ,\ldots, {\bf v}_N\),对第\(n\)个用户,对数据集\(\{({\bf w}_m, r_{nm})\}\)求解一个线性回归模型,更新\({\bf v}_n\)
其实,前面讲的自动编码器也隐含了矩阵分解的思想。类比于矩阵分解的假设函数\({\rm R \approx V^\mathsf{T}W}\),自动编码器的假设函数也可以写为\({\rm X \approx W(W^{\mathsf{T}}X)}\)。两者都是一种线性神经网络,在隐含层使用\(\tilde{d}\)个节点。只不过自动编码器的误差函数是在所有\(x_{ni}\)上做测量,而矩阵分解只在已知\(r_{nm}\)上做测量,而且前者能得到全局最优解,后者只能得到局部最优解。总而言之,自动编码器可以看作是矩阵分解的一种特殊形式
随机梯度下降
上述问题也可以用随机梯度下降(SGD)来求解:从数据集中选取一条数据,在这条数据上算梯度,做梯度下降。这种算法的效率非常高,而且易于实现,易于扩展到其它误差函数上
首先,写出对每一条数据的误差函数 \[ {\rm err}({\rm user\ }n, {\rm movie\ }m, {\rm rating\ }r_{nm}) = (r_{nm} - {\bf w}_m^{\mathsf T}{\bf v}_n)^2 \] 其梯度非常好计算 \[ \begin{align*} \nabla_{ {\bf v}_n}{\rm err} &= -2(r_{nm} - {\bf w}_m^{\mathsf T}{\bf v}_n){\bf w}_m \\ \nabla_{ {\bf w}_m}{\rm err} &= -2(r_{nm} - {\bf w}_m^{\mathsf T}{\bf v}_n){\bf v}_n \end{align*} \] 有趣的是,这两项梯度都正比于残差与另一组变量向量的乘积
套用前面讲过的SGD算法,使用SGD求解矩阵分解的过程可以写为
随机初始化\(\tilde{d}\)维向量\(\{ {\bf w}_m\}, \{ {\bf v}_n\}\)
对\(t = 0,1,\ldots, T\)
在所有已知的\(r_{nm}\)里随机选取一个\((n, m)\)
计算残差\(\tilde{r}_{nm} = (r_{nm} - {\bf w}_m^\mathsf{T}{\bf v}_n)\)
SGD更新 \[ \begin{align*} {\bf v}_n^{\rm new} &\leftarrow {\bf v}_n^{\rm old} + \eta \cdot \tilde{r}_{nm} {\bf w}_m^{\rm old} \\ {\bf w}_m^{\rm new} &\leftarrow {\bf w}_m^{\rm old} + \eta \cdot \tilde{r}_{nm} {\bf v}_n^{\rm old} \end{align*} \]
如果要求解的是大规模矩阵分解问题,SGD非常有效
台大团队在参加2011年KDD Cup比赛时用到的就是SGD矩阵分解,不过他们根据问题的场景做了一点有针对性的修改。这次比赛是根据用户之前一段时间的打分去预测后面一段时间的打分,也就是说训练数据的时间戳要比测试数据早一些。在运行SGD时,实际上最后\(T'\)次迭代里算法会倾向于把它在这段时间里看到的数据效果做好,因此台大队会故意让时间戳较晚的数据在比较靠后的迭代中训练。这意味着,如果了解了模型使用最优化的方式和里面的技巧,那么就能够在实际应用时修改算法以使其更符合问题的需要
特征提取模型小结
从神经网络开始所讲的模型基本都可以称为是特征提取模型。所谓特征提取模型,指的是在送入最终模型之前,将特征变换的过程也纳入学习过程,学习如何表示数据才能有更好的结果。例如在神经网络里,对数据的变换是隐藏层的权重\(w_{ij}^{(\ell)}\),在RBF网络里是\(\boldsymbol{\mu}_m\)(其中KNN是RBF网络的特例),在矩阵分解里则是\({\bf v}_n\)(也可以是\({\bf w}_m\))。从另一个角度看,AdaBoost或者GBDT也有一点特征提取模型的味道,这里对数据的变化是所有基分类器
不同的模型也有一些提取特征的技巧:Boosting算法里是函数梯度下降,神经网络和深度学习里是反向传播+SGD以及自动编码器,RBF网络里是K均值聚类,矩阵分解里是交替最小二乘,而KNN是“偷懒学习”(在测试时才遍历训练集作比较)
特征提取模型的优点是容易使用,减轻了人类提取特征的负担,而且如果使用了足够多的隐藏变量,模型的能力通常比较强;缺点是问题通常不是凸优化问题,比较难以优化,难以达到全局最优解,而且容易过拟合,需要合适的正则化方法或者验证方法。因此,这些模型用起来一定要小心
