正则化的假设集
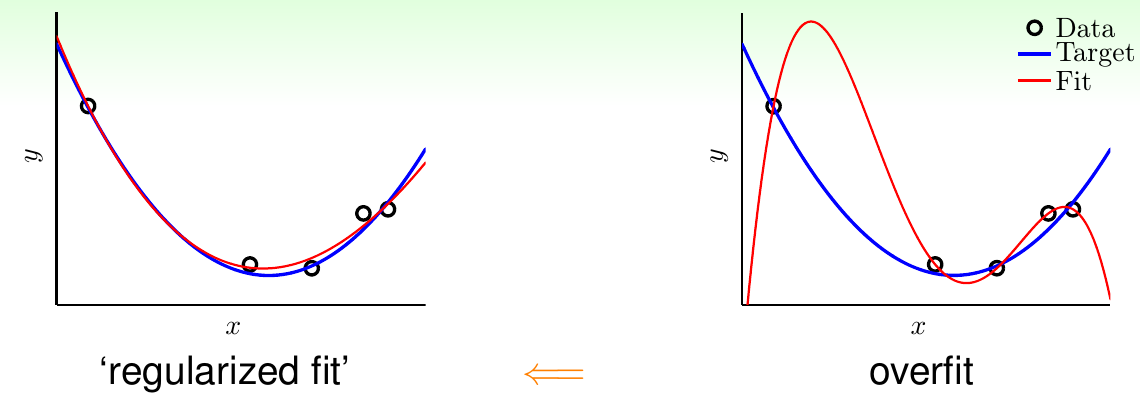
如上图所示,右边给出的就是在上讲中经常提到的过拟合现象,可以看到拟合的曲线(红线)与目标函数图像(蓝线)差别特别大。正则化的目的是对复杂的模型进行调整,使其也可以逼近比较简单的模型。上图左边给出的就是正则化的效果示意,可以发现经过正则化以后,函数光滑了许多,也与目标函数接近了许多。其思想是,从高次多项式假设集合逐步“走回”低次多项式假设集合。“正则化”这个概念来自于早期函数逼近这个领域,以解决其中ill-posed问题
那么如何完成这个“走回”的操作?回想之前给出的对\(x \in \mathbb{R}\)做\(Q\)次多项式变换的方法\(\boldsymbol{\Phi}_Q(x) = (1, x, x^2, \ldots, x^Q)\),为了方便起见,这里不再将在转换后空间\(\mathcal{Z}\)中训练得到的权重记为\(\tilde{\bf w}\),而是直接记为\(\bf w\)。由前面的介绍,\(\mathcal{H}_{10}\)中的\(\bf w\)的形式和\(\mathcal{H}_2\)中的\(\bf w\)的形式可以各自表示为: \[ \begin{align*} \mathcal{H}_{10} &: w_0 + w_1x + w_2x^2 + w_3x^3 + \ldots + w_{10}x^{10} \\ \mathcal{H}_2 &: w_0 + w_1x+w_2x^2 \end{align*} \] 从这个角度看,\(\mathcal{H}_2\)可以看作是\(\mathcal{H}_{10}\)加上了一些限制\(w_3 = \ldots = w_{10}=0\)而成。因此,前面的这个“走回”操作,其实就是加入一些限制。从最优化问题的角度来看,使用\(\mathcal{H}_{10}\)求解回归问题,其对应的最优化表达法为 \[ \min_{ {\bf w} \in \mathbb{R}^{10 + 1}}E_{\rm in}({\bf w}) \] 而使用\(\mathcal{H}_2\)求解回归问题,从某种意义上讲,就是 \[ \begin{align*} \min_{ {\bf w} \in \mathbb{R}^{10 + 1}} &\hspace{2ex}E_{\rm in}({\bf w}) \\ {\rm s.t.} &\hspace{2ex} w_3 = w_4 = \ldots w_{10} = 0 \end{align*} \] 注意到\(\mathcal{H}_2\)是让\(\mathcal{H}_{10}\)的8个高次项系数为0。可以不这么教条,对这个限制条件做一点放松,使得其不是所有高次项全为0,而是有任意至少8个项系数为0(即最多有三个项系数不为0)。这样得到的新假设集合记做\(\mathcal{H}_2'\),则其对应的最优化问题为 \[ \begin{align*} \min_{ {\bf w} \in \mathbb{R}^{10 + 1}} &\hspace{2ex}E_{\rm in}({\bf w}) \\ {\rm s.t.} &\hspace{2ex} \sum_{q=0}^{10}[\![w_q \not= 0]\!] \le 3 \end{align*} \] 这三个假设集之间的关系是\(\mathcal{H}_2 \subset \mathcal{H}_2' \subset \mathcal{H}_{10}\),因此新得到的这个假设集合表示能力强于\(\mathcal{H}_2\),而且风险程度又弱于\(\mathcal{H}_{10}\),看上去很不错。但是这里最关键的问题是,这个问题是一个NP难问题!
但是退而求其次,可以提出一个类似的最优化问题,即不再限制(至多)有多少个项不为0,而是限制这些系数的平方和小于某个常数。这种提法是有意义的,因为在原始问题里,如果某一项系数为0(或者很接近0),它对系数总体平方和的贡献也有限。因此,上面这个问题可以近似于(非等价于!)如下最优化问题 \[ \begin{align*} \min_{ {\bf w} \in \mathbb{R}^{10 + 1}} &\hspace{2ex}E_{\rm in}({\bf w}) \\ {\rm s.t.} &\hspace{2ex} \sum_{q=0}^{10}w_q^2 \le C \end{align*} \] 记该问题对应的假设集合为\(\mathcal{H}(C)\),注意\(\mathcal{H}(C)\)和\(\mathcal{H}_2'\)有交叉,但是不完全相等。而且对不同的\(C \ge 0\),\(\mathcal{H}(C)\)也有重叠结构: \[ \mathcal{H}(0) \subset \mathcal{H}(1.126) \subset \ldots \subset \mathcal{H}(1126) \subset \ldots \subset \mathcal{H}(\infty) = \mathcal{H}_{10} \] 称\(\mathcal{H}(C)\)这样的假设集合为正则化的假设集合,其最优解为正则化的假设,记为\({\bf w}_{\rm REG}\)
权重衰减的正则化方法
如何解这个加了限制的最优化问题?首先可以把问题转化为向量和矩阵形式。向量形式为 \[ \begin{align*} \min_{ {\bf w} \in \mathbb{R}^{Q+1}} &\hspace{2ex}E_{\rm in}({\bf w}) = \frac{1}{N}\sum_{n=1}^N({\bf w}^\mathsf{T}{\bf z}_n - y_n)^2 \\ {\rm s.t.} &\hspace{2ex}\sum_{q=0}^Q w_q^2 \le C \end{align*} \] 对应的矩阵形式为 \[ \begin{align*} \min_{ {\bf w} \in \mathbb{R}^{Q+1}} &\hspace{2ex}E_{\rm in}({\bf w}) = \frac{1}{N}({\rm Z}{\bf w} - {\bf y})^\mathsf{T}({\rm Z}{\bf w} - {\bf y}) \\ {\rm s.t.} &\hspace{2ex} {\bf w}^\mathsf{T}{\bf w} \le C \end{align*} \] 从几何意义上讲,这个限制条件是把\(\bf w\)限制在了一个球心为原点,半径为\(\sqrt{C}\)的超球体里
如何求解这个问题?如果没有条件限制,直接让\(\bf w\)沿着\(-\nabla E_{\rm in}({\bf w})\)的方向滚下去,滚到谷底就得到了\({\bf w}_{\rm LIN}\)
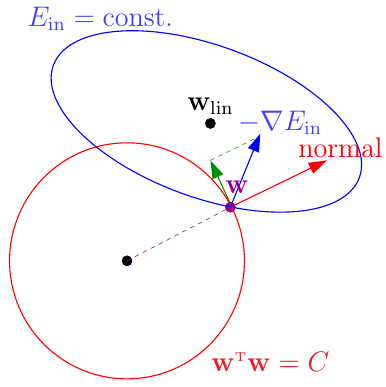
如上图,如果没有正则化项,蓝线就是(某一时刻)\(E_{\rm in}\)的等高线,蓝色的箭头是\(\bf w\)变化的方向。加入正则化条件以后,\(\bf w\)只能在红圈里(或边上),因此大部分情况下\(\bf w\)应该都在红圈上。假设此时\(\bf w\)已经在红圈上,判断其是否达到最优解的方法就是看它是否还能沿着\(-\nabla E_{\rm in}\)的方向往下滚。但是限制条件又规定\(\bf w\)不能滚出球(即沿着红色箭头的方向移动),只能沿着垂直于球法向量的方向移动(即绿色箭头的方向)。这样一来,如果\(-\nabla E_{\rm in}\)这个方向可以沿着绿色箭头的方向分出一个分量,\(\bf w\)沿着该分量方向移动的话,就可以同时满足 i) 受条件\({\bf w}^\mathsf{T}{\bf w} = C\)这个条件限制 ii) 减小\(E_{\rm in}\) 这两个要求。因此,最优的\({\bf w}_{\rm REG}\)肯定与\(-\nabla E_{\rm in}({\bf w}_{\rm REG})\)方向平行(否则还可以继续往下滚),即 \[ -\nabla E_{\rm in}({\bf w}_{\rm REG}) \propto {\bf w}_{\rm REG} \] 将这个比值设为\(\frac{2\lambda}{N}\),则加入了正则化项以后,最优化问题实际上就是要求解\({\bf w}_{\rm REG}\)满足 \[ \nabla E_{\rm in}({\bf w}_{\rm REG}) - \frac{2\lambda}{N} {\bf w}_{\rm REG} = 0 \] 这里\(\lambda > 0\)实际上是拉格朗日乘子,上面实际上给出了拉格朗日乘子的几何意义。假设\(\lambda\)已知,上面这个式子其实就是关于\({\bf w}_{\rm REG}\)的一个线性方程。代入梯度的定义,有 \[ \frac{2}{N} ({\rm Z}^\mathsf{T}{\rm Z}{\bf w}_{\rm REG} - {\rm Z}^\mathsf{T}{\bf y}) + \frac{2\lambda}{N}{\bf w}_{\rm REG} = 0 \] 求解可得 \[ {\bf w}_{\rm REG} = ({\rm Z^\mathsf{T}Z + \lambda I})^{-1}{\rm Z}^\mathsf{T}{\bf y} \] 给定\(\lambda > 0\),由于\(\rm{Z^\mathsf{T}Z}\)是半正定矩阵,\(\lambda I\)是正定矩阵,两者相加也是正定矩阵,因此\({\rm Z^\mathsf{T}Z + \lambda I}\)永远存在逆矩阵,上式总可求解
这个回归在统计上被称为是岭回归
岭回归还可以从另一个角度推导:求解\(\nabla E_{\rm in} = 0\)对应的是要最小化\(E_{\rm in}({\bf w})\),如果加上限制条件,那么对限制条件求积分,其实就是为了最小化\(E_{\rm in}({\bf w}) + \frac{\lambda}{N} {\bf w}^\mathsf{T}{\bf w}\)。其中加上的这一项称为正则化项,加上正则化项以后的误差称为增强误差,记为\(E_{\rm aug}({\bf w})\)。增强误差项包含了限制条件,又没有显式给出限制条件,比较容易求解。因此,正则化的过程也可以看作是最小化增强误差的过程,即对给定的\(\lambda \ge 0\)求解 \[ {\bf w}_{\rm REG} \leftarrow \mathop{ {\rm arg}\min }_{\bf w} E_{\rm aug}({\bf w}) \] (笔记注:这块感觉讲得有点太细致了,如果知道拉格朗日乘子的意义,这种转化是显然的)
下图中给出了正则化项系数\(\lambda\)对模型效果的影响。可以看出,\(\lambda\)越大,正则得越狠,模型越容易欠拟合。实际使用时,一点点正则化项就可以起到很大的作用
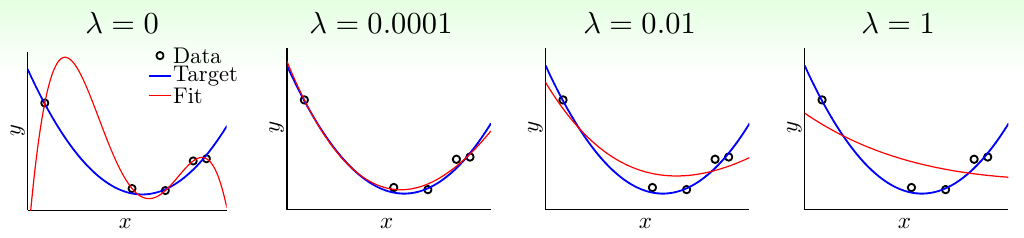
进一步地,称\(+\frac{\lambda}{N}{\bf w}^\mathsf{T}{\bf w}\)为权重衰减的正则化方法。因为正则化项系数\(\lambda\)越大,\(\bf w\)就会更小,其范数\(C\)也会越小
这种方法可以和任意特征变换方式和线性模型搭配使用,例如跟Logistic回归搭配使用
第12页幻灯片给出了一个多项式特征变换的细节:如果按照普通的\(1, x, x^2 , \ldots\)这样变换,当\(x \in [-1, 1]\)时,其高次项的值会特别小,因此对应的权重系数会比较大。为了避免这种现象出现,讲义中使用了\(1, L_1(x), L_2(x), \ldots\)的变换方式,其中\(L_i(x)\)对应为勒让德多项式中的第\(i\)个表达式。勒让德多项式的各个组成元素也是多项式空间的一组正交基
正则化与VC维
一个很自然的问题就是,正则化方法和之前介绍的VC维有什么关系。我们的出发点是要解一个受限制的\(E_{\rm in}\)的问题,而由于\(\lambda\)与\(C\)有对应关系,因此解带有限制的最优化问题其实就等价于解一个无限制,但是相对\(E_{\rm in}\)更大的\(E_{\rm aug}\)。而原始问题对应的VC保证是,\(E_{\rm out}({\bf w})\)会比\(E_{\rm in}({\bf w})\)加上一个对复杂性的惩罚项\(\Omega(\mathcal{H}(C))\),即\(E_{\rm out}({\bf w}) \le E_{\rm in}({\bf w}) + \Omega(\mathcal{H}(C))\)。最小化\(E_{\rm aug}({\bf w})\)的过程也是在间接地满足这个VC保证(因为每个\(\lambda\)都有对应的\(C\)),而且由于去掉了限制条件,还考察了所有可能的\(\bf w\)
因此,被放大的误差与VC上界存在一定的相似性:被放大的误差是向\(E_{\rm in}\)加上了一项,VC上界也是向\(E_{\rm in}\)加上了一项。被放大的误差所加的一项\(\frac{\lambda}{N}{\bf w}^\mathsf{T}{\bf w}\)说明了某个假设有多复杂(这个假设越复杂,正则项就会越大,从直觉来看,曲线就越弯曲),而VC上界加的项\(\Omega(\mathcal{H})\)说的是整个假设集合有多复杂。如果将\({\bf w}^\mathsf{T}{\bf w}\)记为\(\Omega({\bf w})\),将其看作是某个模型的复杂度,同时考虑一个前提:假设某个假设很复杂,那么它肯定处在一个复杂的假设集合中。这样一来,\(\frac{\lambda}{N}\Omega({\bf w})\)就是\(\Omega({\mathcal{H})}\)的一个缩影,而\(E_{\rm aug}\)比起\(E_{\rm in}\)也是\(E_{\rm out}\)更好的代理。所以,最小化\(E_{\rm aug}\)是最小化\(E_{\rm out}\)的一个更好的启发式方法,这种做法给予我们更自由在\(\mathcal{H}\)上选择\(\bf w\)的能力
再从另一个角度去思考所得到模型的复杂性。对优化问题 \[ \min_{ {\bf{w}} \in \mathbb{R}^{\tilde{d}+1}} E_{\rm aug}({\bf w}) = E_{\rm in}({\bf w}) + \frac{\lambda}{N}\Omega({\bf w}) \] 名义上模型的复杂度\(d_{\rm VC}(\mathcal{H}) = \tilde{d} + 1\),因为考虑了所有\(\bf w\) 。但是实际上由于\(\lambda\)和\(C\)隐含的对应性,只有一少部分属于\(\mathcal{H}(C)\)的\(\bf w\)才会被考虑,因此模型的实际复杂度只有\(d_{\rm VC}(\mathcal{H}(C))\)。这样,可以引入模型的“有效VC维”这个概念,记为\(d_{\rm EFF}(\mathcal{H, A})\)。其中\(\mathcal{H}\)说明候选的假设集仍然是完整的假设集,而\(\mathcal{A}\)则代表了算法选择模型的方法。所以即便\(d_{\rm VC}(\mathcal{H})\)很大,如果用了正则化的算法\(\mathcal{A}\),实际的\(d_{\rm EFF}(\mathcal{H, A})\)也会很小
常见的正则项
前面介绍的方法里,正则项用的都是\({\bf w}^\mathsf{T}{\bf w}\)。那么正则项有没有可能有别的选择?\(\bf w\)有没有别的形式的条件?由于目标函数的不可预知性,我们无法提前给出最好的假设会是什么样。不过退而求其次,可以给出目标函数应该处于什么方向上。总体来讲,设计正则项有如下指导性原则
- 正则项的设计应该与目标相关。例如假设要让正则项对称,可以设为\(\sum [\![q{\rm\ is\ odd}]\!] w_q^2\)
- 正则项的设计应该看上去合理。由于无论是随机误差还是决定性误差都不平滑,因此正则项应该使最后的\(\bf w\)更平滑或更简单
- 正则项的设计应该比较友好,易于优化
当然,即便正则项设计得不好,也可以用\(\lambda\)来控制,至少可以保证模型不受正则项影响
可以看到,正则项设计的三项原则和误差函数设计的三项原则异曲同工,都包括了目标相关性、合理性和友好性这三个点。它们也是设计机器学习算法时需要注意的关键
之前介绍过L2正则化项,其形式为\(\Omega({\bf w}) = \sum_{q=0}^Q w_q^2 = |\!|{\bf w}|\!|_2^2\)。这是一个凸函数,而且处处可微,因此易于优化。另一种常见的正则化项称为L1正则化项:前面L2正则化项用的是\(\bf w\)的L2范数,同理L1正则化项用的是\(\bf w\)的L1范数,即\(\Omega({\bf w}) = \sum_{q=0}^Q |w_q| = |\!|{\bf w}|\!|_1\)。注意这个函数仍然是凸函数,但是在\(w_i = 0\)时是不可微的,因此优化起来要稍微麻烦一点。那为什么它还广受青睐?参考下图
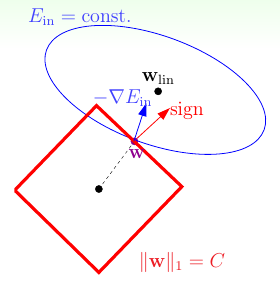
类似之前提到的L2正则化的原理,只有当\(\bf w\)的移动方向\(-\nabla E_{\rm in}\)(这里是蓝色箭头)与法向量(这里是红色箭头)平行时,\(\bf w\)才达到最优解。当\(\bf w\)在正方形的边上时,这种状态一般不会发生,因此总会有\(\bf w\)的一个分量拉着\(\bf w\)前进,直到到达正方形的顶点处。而在顶点时,说明有一些\(w_i\)其值为0,这意味着使用L1正则项会得到比较稀疏的解,计算效率更高
最后,下图给出了当噪声不同的时候,最优正则项系数的取值
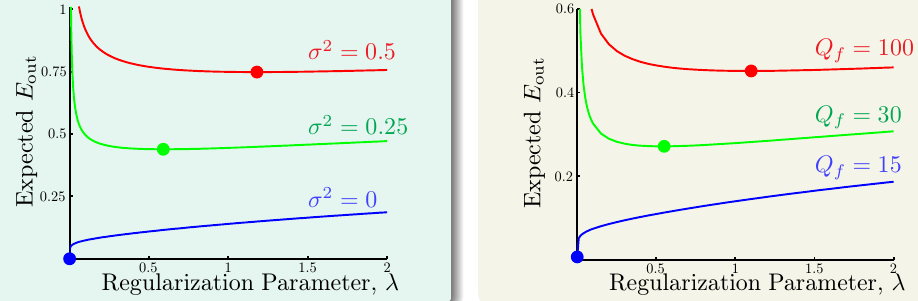
可以看到,无论是随机噪声还是决定性噪声,噪声越大,\(\lambda\)就应该越大。但是我们并不知道噪声有多大,那么\(\lambda\)应该如何选择?这个问题留待下讲作答
