什么是过拟合
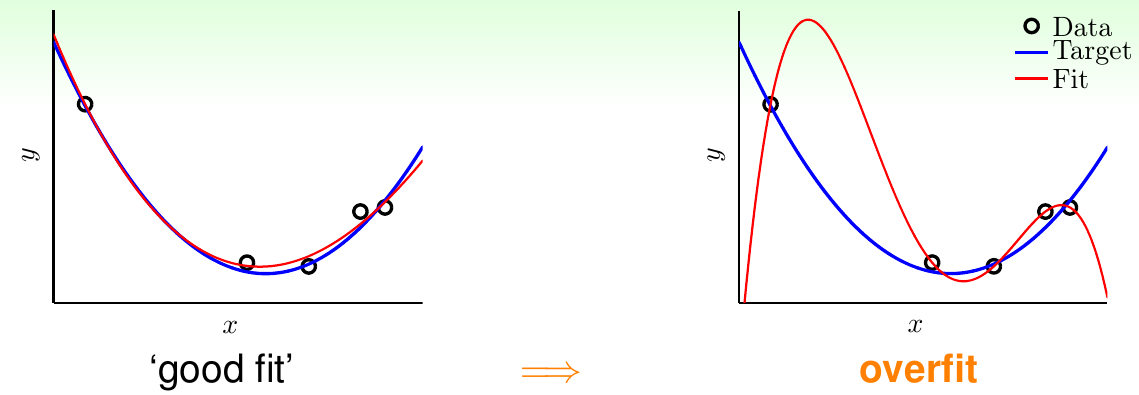
假设现在要做一个一维数据集的回归分析,数据集一共有5个点,目标函数是一个二次函数,所有的\(x_i, i = 1, 2, 3, 4, 5\)都是随机产生,其对应的标签\(y_i\)是对应的目标函数值加上一点微小的噪声。由于拿到数据集以后并不知道目标函数的形式,因此一种思路是使用前面提到的多项式变换,引入一些四维特征。这样,拟合出的四维函数\(g\)可以完美地穿过这五个点,做到\(E_{\rm in}(g) = 0\)。但是显而易见,这种情况下\(E_{\rm out}(g)\)会非常大,导致了比较差的泛化结果。前面曾经提到过,当\(h\)的VC维特别大时,就会导致这种情况发生。只有当\(h\)的VC维取到最优情况\(d_{\rm VC}^\ast\)时,才能使得\(E_{\rm in}\)和\(E_{\rm out}\)都取到最小。当\(h\)的VC维很大,超过\(d_{\rm VC}^\ast\)时,随着VC维的升高,\(E_{\rm in}\)仍然会降低,但是\(E_{\rm out}\)会不降反增。称这种现象为过拟合。对应地,当\(h\)的VC维比较小,没有达到\(d_{\rm VC}^\ast\)时,随着VC维的减小,\(E_{\rm in}\)和\(E_{\rm out}\)都会增加。称这种现象为欠拟合。下图给出了一个关于过拟合的状况示例
以上所讲的概念可以用开车的过程做类比——
- 过拟合,类似于出车祸
- 使用太复杂,\(d_{\rm VC}\)太大的模型,类似于开太快
- 数据中噪声比较多,类似于路面情况不平
- 数据集大小\(N\)比较小,类似于司机对路面状况观察比较有限,对路况不熟
噪声与数据集大小的角色
接下来进行更多的实验来探索过拟合这一现象。我们设计了两个不同的目标函数和数据集,其分别为
- 目标函数是某个十次多项式,数据产生时加入一些噪声,产生15个数据点
- 目标函数是某个50次多项式,数据产生时不加入噪声,产生15个数据点
然后,对这两个数据集,都使用二次多项式和十次多项式拟合,观察这两个模型的效果。记二次多项式模型为\(g_2 \in \mathcal{H}_2\),十次多项式模型为\(g_{10} \in \mathcal{H}_{10}\)。下图给出了两组方法在两组数据集上的效果比较。绿色为\(g_2\),红色为\(g_{10}\)
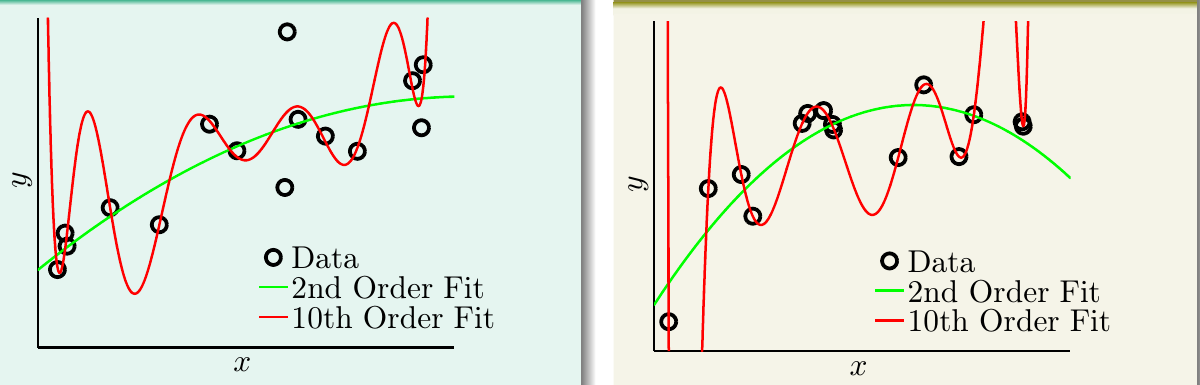
对于左边的数据集,\(g_2\)的\(E_{\rm in}\)为0.050,\(g_{10}\)的\(E_{\rm in}\)为0.034,后者稍胜。但是前者的\(E_{\rm out}\)为0.127,后者达到了9。对于右边的数据集,\(g_2\)的\(E_{\rm in}\)为0.029,\(g_{10}\)的\(E_{\rm in}\)为0.00001。而\(E_{\rm out}\)的差距更多:前者0.120,后者居然达到了7680!可以看到,在这样两个由高次多项式产生的数据集上,使用高次多项式拟合出来的模型仍然发生了严重的过拟合现象。尤其是对于由十次多项式产生的数据集,按照道理,二次多项式模型应该没有能力在其上获得很好的效果,但是其\(E_{\rm out}\)却的确取得了一个比较令人满意的结果。应该如何解释这种“以退为进”的现象?
这里回顾一下对不同的假设集合,其\(E_{\rm in}\)/\(E_{\rm out}\)与数据集大小\(N\)之间的关系,可见下图

如图所示,所有的二次多项式假设集\(\mathcal{H}_2\)和所有的十次多项式假设集\(\mathcal{H}_{10}\)都遵循了同样的规律:
- 随着数据量\(N\)的增长,\(E_{\rm out}\)会下降,\(E_{\rm in}\)会上升。最后当\(N\rightarrow \infty\)时,\(|E_{\rm in} - E_{\rm out}| \rightarrow 0\)
- \(E_{\rm in}\)永远小于\(E_{\rm out}\)。因为模型在学习数据时,总会学习到其所看见的数据中的噪声,并对其进行拟合。而对看不见的数据就难以对噪声拟合很好。由于假设数据集噪声的期望为0,因此当偏向一面时,就会远离另一面
- \(\mathcal{H}_{10}\)的\(E_{\rm in}\)永远低于\(\mathcal{H}_2\)的
除此以外,当\(N\rightarrow \infty\)时,更复杂的\(\mathcal{H}_{10}\)的确会得到更好的\(E_{\rm out}\)。因为模型VC维更大,能力更强。但是当\(N\)不够大时,\(\mathcal{H}_{10}\)的\(E_{\rm out}\)会非常大。实际上,图中显示,当\(N\)比较小时(落在灰色区域),\(E_{\rm out}(\mathcal{H}_{10}) > E_{\rm out}(\mathcal{H}_{2})\),表现出了过拟合(“聪明反被聪明误”)。因此,数据量不够大时,总应该使用更简单的模型!
但是这里有一个问题:对于第二个数据集,明明数据集里没有噪声,为什么简单的模型表现也会好?实际上,模型复杂度提升以后,其效果可以看做是类似于往数据集里添加了噪声。这一情况将在下节继续探讨
确定性噪声
接下来看一个更细节的实验,来观察何时会发生过拟合。想象数据产生的过程为目标函数加上一些随机噪声,即\(y = f(x) + \epsilon\)。其中噪声的分布为方差为\(\sigma^2\)的高斯分布。因此有 \[ y \sim {\rm Gaussian}\left(\underbrace{\sum_{q=0}^{Q_t}\alpha_qx^q}_{f(x)}, \sigma^2\right) \] 这里,\(\sigma^2\)控制了噪声的强度,\(f(x)\)控制了模型的复杂度。记\(f(x)\)的复杂度为\(Q_f\),其与多项式的最高次数挂钩:如果\(f(x)\)是10次多项式,\(Q_f = 10\);如果\(f(x)\)是50次多项式,\(Q_f = 50\)。记实验使用的数据量为\(N\),这里要探索不同的\((N, \sigma^2)\)和不同的\((N, Q_f)\)对过拟合的影响
这里,候选的假设集合仍然和前面的设置一样,分别是\(g_2 \in \mathcal{H}_2\)和\(g_{10} \in \mathcal{H}_{10}\)。由前面的分析,\(g_{10}\)过拟合的概率比较大,那么这个过拟合的程度如何衡量?这里使用的方法是\(E_{\rm out}(g_{10}) - E_{\rm out}(g_2)\)
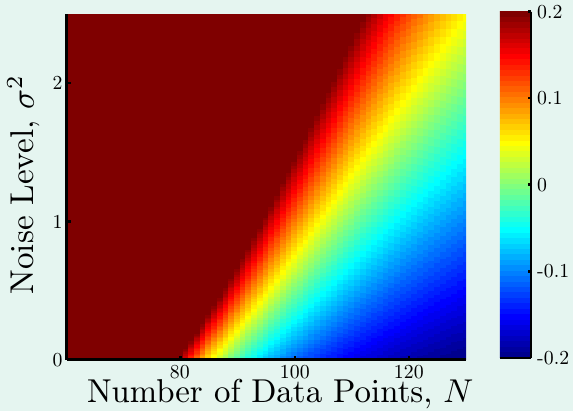
首先看固定模型复杂度\(Q_f = 20\)以后,过拟合度与\(N\)和\(\sigma^2\)的关系。这里颜色越深,过拟合程度越严重。显见当样本量小,误差大的时候,过拟合比较严重;而样本量大,误差小的时候,不太容易过拟合
接着看固定噪声强度\(\sigma^2 = 1\)以后,过拟合度与\(Q_f\)和\(N\)的关系。
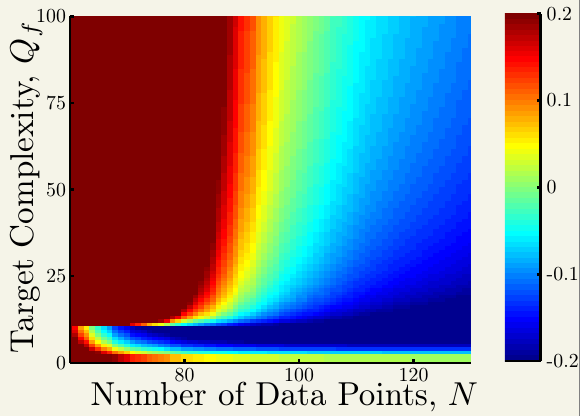
大部分情况下,这种情况与前述实验类似,也是左上角容易过拟合,右下角不容易过拟合。这再次说明模型复杂度可以扮演噪声的角色。称前面施加的正态噪声为随机噪声,模型复杂度带来的噪声为确定性噪声,可以看出造成过拟合的因素有如下几条
- 数据量太小
- 随机噪声太大
- 确定性噪声太大
- 使用的模型比目标函数更复杂(注意第二幅图左下角)
过拟合常常存在,并很容易发生
可以从另一个角度去理解确定性噪声:当目标函数\(f\)过于复杂,\(f\notin \mathcal{H}\)时,\(f\)的一些性质不能被\(\mathcal{H}\)中的任意假设所描述(例如一个10次多项式,它的一些弯折是无法被二次多项式所描述的)。因此\(\mathcal{H}\)中最好的假设\(h^\ast\)和\(f\)之间的差距就是确定性噪声。实际上,确定性噪声与随机噪声差别不大(参考伪随机数生成器的原理),不过它并不是完全随机的,依赖于\(\mathcal{H}\)和给定的\(\bf x\)
应对过拟合
在知道了过拟合的概念和产生原因以后,就可以设计对过拟合的应对方案。仍以开车作比喻,有
- 先使用简单模型训练,类似于开慢车
- 对数据做一些清洗,类似于使用更准确的路况
- 观察数据,根据对数据的理解,按照相同规律产生一些新的数据(data hinting),类似于多看一些路况
- 使用正则化方法,类似于踩刹车
- 验证模型,类似于常看仪表盘
其中正则化和模型验证在之后讲解。数据清洗包括了两种方法,一种是矫正数据的标签,另一种是直接把脏数据移除。不过这种方法对模型的影响不定,可能非常有限
对于data hinting,一种很经典的例子就是在手写数字识别问题中,对已有的手写数字图像做翻转或者倾斜,产生一些新的例子(称作虚拟的例子)。这里要注意,这种方法产生的数据已经不是\(\overset{ {\rm i.i.d.}}{\sim} P({\bf x}, y)\),因此加进来的数据要有道理,而且不能离原有数据太远
