二次函数假设
二维平面上,解决二元分类问题的分类器可以看做是一条直线(在更高维空间上,是一个超平面),其核心思想是使用权重向量\(\bf w\)对输入\(\bf x\)算一个分数\(s = {\bf w}^\mathsf{T}{\bf x}\),然后对得到的分数做进一步处理。这种做法的好处是其VC维能够受到控制,因此\(E_{\rm in}\)和\(E_{\rm out}\)不会差太远。但是对于某些数据\(\mathcal{D}\),例如下图中给出的这种,可以发现无论怎么画线,都很难很好地将数据集分开。也就是说,不论怎么画线,\(E_{\rm in}\)都会非常大,因此\(E_{\rm out}\)也会很大。这样,线性模型在这样的数据集上无论如何都学不好。基于这样的状况,如何突破线性模型的限制成为了必须要解决的问题
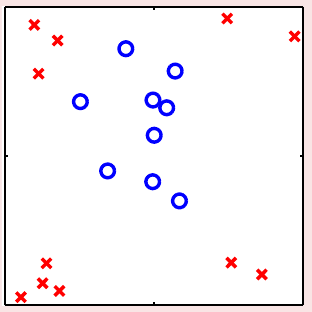
经过观察,可以发现,尽管上图中的\(\mathcal{D}\)并不是线性可分,但是可以用一个圆(半径为\(\sqrt{0.6}\) )将这些数据都分开,因此,可以用假设函数 \[ h_{\rm SEP}({\bf x}) = {\rm sign}(-x_1^2 - x_2^2 + 0.6) \] 来对这个数据集分类。但是我们需要重头推导一遍圆形可分的数据集的算法吗?并不用。如果将上式中的未知数和变量写明确,可以转化为如下形式 \[ h({\bf x}) = {\rm sign}\left(\underbrace{0.6}_{\tilde{w}_0} \cdot \underbrace{1}_{z_0} + \underbrace{(-1)}_{\tilde{w}_1} \cdot \underbrace{x_1^2}_{z_1} + \underbrace{(-1)}_{\tilde{w}_2} \cdot \underbrace{x_2^2}_{z_2}\right) \] 如上式所示,将\(x_1^2\)视作新变量\(z_1\),\(x_2^2\)视作新变量\(z_2\),则上式可以简写为 \[ h({\bf z}) = {\rm sign}(\tilde{\bf w}^\mathsf{T}{\bf z}) \] 这意味着,使用上面的变换方法,在\(\{({\bf x}_n, y_n)\}\)上圆形可分的数据,在\(\{({\bf z}_n, y_n)\}\)上会变得线性可分。这种将\(\mathcal{X}\)的点变换为\(\mathcal{Z}\)中点的方法(记为\(\boldsymbol{\Phi}\)) \[ {\bf x} \in \mathcal{X} \overset{\boldsymbol{\Phi}}{\longmapsto} {\bf z}\in \mathcal{Z} \] 称为一个(非线性)特征变换
既然\(\mathcal{X}\)上的圆形分类器都可以用\(\mathcal{Z}\)上的一条直线来表示,那么反过来是不是对的?即\(\mathcal{Z}\)上的一条直线是不是对应了\(\mathcal{X}\)上的一个圆?按照之前\(\boldsymbol{\Phi}\)的做法,有 \[ (z_0, z_1, z_2)= {\bf z} = \boldsymbol{\Phi}({\bf x}) = (1, x_1^2, x_2^2) \] 那么 \[ h({\bf x}) = \tilde{h}({\bf z}) = {\rm sign}(\tilde{\bf w}^\mathsf{T}\boldsymbol{\Phi}({\bf x})) = {\rm sign}(\tilde{w}_0 + \tilde{w}_1x_1^2 + \tilde{w}_2x_2^2) \] 根据解析几何的知识,对\(\tilde{\bf w} = (\tilde{w}_0, \tilde{w}_1, \tilde{w}_2)\),尽管\(\mathcal{Z}\)中是一条直线,但根据权重每个分量的取值不同,对应到\(\mathcal{X}\)上可能是不同的二次曲线,例如
- \((0.6, -1, -1)\)对应了一个圆(将圆内的点判断为正例)
- \((-0.6, +1, +1)\)对应了一个圆(将圆外的点判断为正例)
- \((-0.6, -1, -2)\)对应了一个椭圆
- \((-0.6, -1, +2)\)对应了一个双曲线
- \((0.6, +1, +2)\)这个分类器会将所有样本都分为正例
注意这里尽管得到的二次曲线不同,但是它们会有一些共同的限制。例如,当\(w_1 = w_2\)且与\({w_0}\)异号时,得到的圆虽然半径不同,但是其圆心始终会在原点上。要打破这样的限制,就需要\(\boldsymbol{\Phi}\)做的变换包含了\(x_1\)与\(x_2\)二次(及更低次)组合的各种形式,即\(\boldsymbol{\Phi}_2({\bf x}) = (1, x_1, x_2, x_1^2, x_1x_2, x^2_2)\)。重新记\(\mathcal{X}\)经\(\boldsymbol{\Phi}_2\)变换后得到的空间为\(\mathcal{Z}\),则假设集合\(\mathcal{H}_{\boldsymbol{\Phi}_2} = \{h({\bf x}): h({\bf x}) = \tilde{h}(\boldsymbol{\Phi}_2({\bf x})){\rm\ for \ some\ linear\ }\tilde{h}{\rm\ on\ }\mathcal{Z}\}\)就可以实现\(\mathcal{X}\)中的所有二次曲线,包括直线等退化情况
非线性变换
之前说到,\(\mathcal{X}\)空间中的非线性分类问题,在找到一个合适的从\(\mathcal{X}\)到\(\mathcal{Z}\)上的非线性变换\(\boldsymbol{\Phi}\)以后,可以用\(\mathcal{Z}\)空间上的感知机来做分类。如何训练\(\mathcal{Z}\)上的感知机?参考之前使用数据\(\{({\bf x}_n, y_n)\}\)训练\(\mathcal{X}\)上感知机的方法,用经过非线性变换得到的新数据\(\{({\bf z}_n = \boldsymbol{\Phi}({\bf x}_n), y_n)\}\)进行训练即可。整个步骤描述如下
- 将原始数据\(\{({\bf x}_n, y_n)\}\)使用\(\boldsymbol{\Phi}\)变换为\(\{({\bf z}_n = \boldsymbol{\Phi}({\bf x}_n), y_n)\}\)
- 使用\(\{({\bf z}_n, y_n)\}\)和你擅长的线性分类算法得到\(\mathcal{A}\)得到一个好的权重\(\tilde{\bf w}\)
- 返回\(g({\bf x}) = {\rm sign}(\tilde{\bf w}^\mathsf{T}\boldsymbol{\Phi}({\bf x}))\)
也可参考如下图例。注意使用非线性变换时一般没有\(\boldsymbol{\Phi}^{-1}\)的那一步,图中加上这一步只是为了加深理解(实际上,\(\boldsymbol{\Phi}\)的反函数是否存在也未可知)

非线性变换是一个独立的提取特征的操作,因此它不一定只能用在二元分类问题上,而是可以和所有其它线性模型相结合。需要注意的是,非线性变换只是得到新特征的一种方法,而特征工程是解决机器学习问题时最重要的“原力”之一
非线性变换的代价
计算/存储代价
假设原始的变量集合\({\bf x} \in \mathcal{X}\)都是\(d\)维的,即\({\bf x} \in \mathbb{R}^d\),要做一个完全的二次变换,即其包含\((x_1, x_2, \ldots, x_d)\)形成的所有二次项、一次项和常数项,得到的\({\bf z} = \boldsymbol{\Phi}_2({\bf x})\)的维度是多少?所有二次项的数目是\({d \choose 2} + d\)(\(x_ix_j, i \not= j\)的项和\(x_i^2\)的项),一次项的数目是\(d\),常数项数目是1,因此最后\(\bf z\)的维度是\(\frac{d^2}{2} + \frac{3d}{2} + 1\)。推广这个结论,假设源数据维度为\(d\) ,做一个完全的\(Q\)次变换,得到的新数据维度\(\tilde{d}\)为\({Q+d \choose Q} = {Q+d \choose d}\),复杂度大概为\(O(Q^d)\)。这也是计算和存储\({\bf z} = \boldsymbol{\Phi}_Q({\bf x})\)和\(\tilde{\bf w}\)的代价
模型复杂度代价
另一方面,特征变换以后,新的权重\(\tilde{\bf w}\)有\(\tilde{d}+1\)个自由变量。由前面提到的VC维和自由变量数之间的关系,\(\mathcal{H}_{\boldsymbol{\Phi}_Q}\)的VC维大概就是\(\tilde{d}+1\)。这意味着当\(Q\)变大时,模型的VC维也会变大。这会带来什么问题?考虑下面这个带噪声的数据集,左边使用线性特征做分类,右边使用四次特征做分类
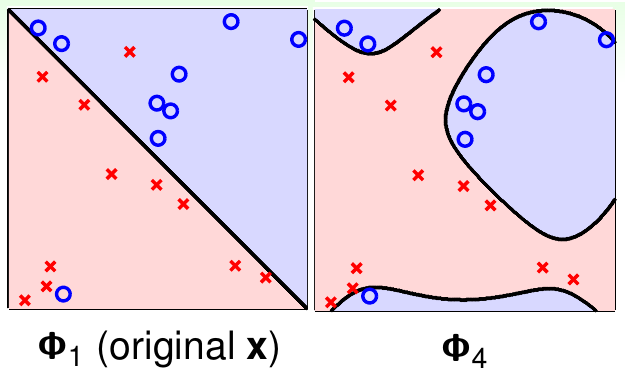
尽管\(\boldsymbol{\Phi}_4\)转换以后分类器可以做到\(E_{\rm in}\)为0,但是看上去\(\boldsymbol{\Phi}_1\)更符合直觉。这又带来了一个均衡问题:低维的\(\tilde{d}(Q)\)可以使\(E_{\rm out}\)与\(E_{\rm in}\)足够接近,但是不能得到足够小的\(E_{\rm in}\);高维的\(\tilde{d}(Q)\)可以得到足够小的\(E_{\rm in}\),但是不能让\(E_{\rm in}\)足够接近于\(E_{\rm out}\)
那么如何选择这个合适的\(Q\)呢?上面这个例子里,可以通过用眼看来选择。但是用眼看总是一个很好的方法吗?先不说当\(d = 10\)时如何用眼偷看资料,仅考虑最开始举的那个例子
- 如果什么都不看,做一个\(\boldsymbol{\Phi}_2\)变换,VC维是6
- 如果看了数据,可以将\({\bf x}\)转化为\({\bf z} = (1, x_1^2, x_2^2)\),这样VC维是3
- 甚至更聪明一点,可以做转化\({\bf z} = (1, x_1^2+x_2^2)\),VC维是2
因此需要意识到一个问题:后来做的这些转换,其VC维降低是因为大脑做了分析而造成的功劳,因此判断VC维的时候得综合考虑,不能忘记人为分析造成的VC维减小
(讲义里最后还有句话:为了能安全地估计VC维,不能先“偷看”数据再决定做什么特征变换\(\boldsymbol{\Phi}\) )
结构化假设集
多项式变换可以递归定义: \[ \begin{align*} \boldsymbol{\Phi}_0({\bf x}) &= (1) \\ \boldsymbol{\Phi}_1({\bf x}) &= (\boldsymbol{\Phi}_0({\bf x}), x_1, x_2, \ldots, x_d) \\ \boldsymbol{\Phi}_2({\bf x}) &= (\boldsymbol{\Phi}_1({\bf x}), x_1^2, x_1x_2, \ldots, x_d^2) \\ \boldsymbol{\Phi}_3({\bf x}) &= (\boldsymbol{\Phi}_2({\bf x}), x_1^3, x_1^2x_2, \ldots, x_d^3) \\ &\cdots \\ \boldsymbol{\Phi}_Q({\bf x}) &= (\boldsymbol{\Phi}_{Q-1}({\bf x}), x_1^Q, x_1^{Q-1}x_2, \ldots, x_d^Q) \\ \end{align*} \] 如果记\(\mathcal{H}_{\boldsymbol{\Phi}_i}\)为\(\mathcal{H}_i\),由上面的递归定义有 \[ \mathcal{H}_0 \subset \mathcal{H}_1 \subset \mathcal{H}_2 \subset \mathcal{H}_3 \subset \ldots \subset \mathcal{H}_Q \] 由于越复杂的变换得到的假设函数能够打散的点越多,因此 \[ d_{\rm VC}(\mathcal{H}_0) \le d_{\rm VC}(\mathcal{H}_1) \le d_{\rm VC}(\mathcal{H}_2) \le d_{\rm VC}(\mathcal{H}_3) \le \ldots \] 如果设\(g_i = \mathop{ {\rm arg}\min}_{h \in \mathcal{H}_i} E_{\rm in}(h)\),则因为越复杂的变换可选的\(h\)越多,有 \[ E_{\rm in}(g_0) \ge E_{\rm in}(g_1) \ge E_{\rm in}(g_2) \ge E_{\rm in}(g_3) \ge \ldots \] 所以是否有\(Q\)越高越好?且慢!第七讲中的图列出了VC维与误差之间的关系。尽管随着VC维的增大,样本内误差会单调减小,但是模型复杂度会增高。当模型的VC维超过最优的\(d_{\rm VC}^\ast\)以后,样本外误差会不降反升。如果上来设计一个很高维度的转换,尽管能做到不错的\(E_{\rm in}\),但是遇到不同的样本模型性能会很差,而且很难做进一步改进。非线性变换(这里主要是多项式变换)的正确打开方式应该是,先从\(\mathcal{H}_1\)试起。如果成功了,那么由于其本身的性质,\(E_{\rm out}\)应该也不会差。即便是效果不好,也可以再逐个尝试\(\mathcal{H}_2\)等等。这样做失去的只有用简单特征训练测试模型时的一点时间,得到的确实比较保险稳妥的结果——而且,大多数情况下,线性模型可能还真挺有效可用的。
