用于二元分类的线性模型
之前提到的三种线性模型都使用了\(s = {\bf w}^\mathsf{T}{\bf x}\)这个函数来计算得分
- 线性分类直接对这个分值取正负号,使用0/1误差来做误差函数。\(E_{\rm in}(\bf w)\)是离散的,优化是NP-hard问题
- 线性回归对这个分值不作处理直接输出,因此值域是\(\mathbb{R}\),误差函数是平方误差。这个\(E_{\rm in}({\bf w})\)优化起来比较友好,能直接得到一个闭合解
- Logistic回归对分值做一个logistic变换\(\theta(s)\),值域是\([0, 1]\),使用交叉熵函数做误差函数。这个\(E_{\rm in}(\bf w)\)可以用梯度下降方法求解
接下来首先探讨一个问题:线性回归或Logistic回归可以用来求解线性分类问题吗?首先要整合一下这些误差函数,将关于\(h, {\bf x}, y\)的函数转化为关于\(s, y\)的函数。其中\(s = {\bf w}^\mathsf{T}{\bf x}, y\in \{-1, +1\}\)
对线性分类问题,有 \[ \begin{align*} &&h({\bf x}) &= {\rm sign}(s) \\ &&{\rm err}(h, {\bf x}, y) &= [\![h({\bf x}) \not = y]\!] \\ &\Rightarrow &{\rm err_{0/1}}(s, y) &= [\![{\rm sign}(s) \not= y]\!] \\ && &=[\![{\rm sign}(ys) \not= 1]\!] \end{align*} \] 对线性回归问题,有 \[ \begin{align*} &&h({\bf x}) &= s \\ &&{\rm err}(h, {\bf x}, y) &= (h({\bf x}) - y)^2 \\ &\Rightarrow&{\rm err_{\rm SQR}}(s, y) &= (s-y)^2 \\ &&&= (ys-1)^2 \end{align*} \] 对Logistic回归问题,有 \[ \begin{align*} &&h({\bf x}) &= \theta(s) \\ &&{\rm err}(h, {\bf x}, y) &= -\ln h(y{\bf x}) \\ &\Rightarrow &{\rm err_{CE}}(s, y) &= \ln(1+\exp(-ys)) \end{align*} \]
可以看到,这三个误差函数里都包括了\(ys\)这一项。那么该项的物理意义是什么?这里\(y\)是正确度,\(s\)是得分,因此两者相乘可以看作是“分类的正确度得分”:两者相乘得到的结果越大,说明越正确;否则说明越不正确。这个做法实际很符合逻辑:假设\({\bf w}^\mathsf{T}{\bf x}\)是一个比较大的正数,那么由Logistic回归的物理意义这说明\(y=1\)的概率会非常大。假设实际上\(y=-1\),那么两者相乘就是一个比较小的负数,说明是有问题的
将上面得到的三个函数图像作到一个坐标系里,可以得到如下的图
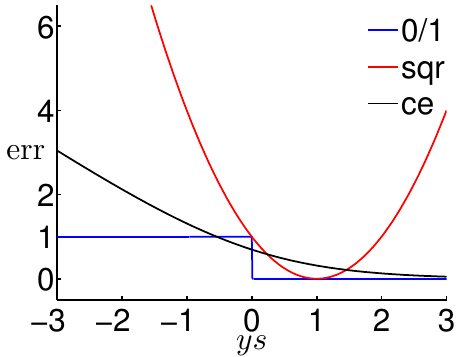
可以看到一些现象:
对于0/1误差函数,如果\(ys \le 0\),说明\(y\)与\(s\)异号,发生了分类错误,因此\({\rm err}_{0/1}\)为1。如果\(ys > 0\),说明\(y\)与\(s\)同号,分类是正确的,\({\rm err}_{0/1}\)为0
对于平方误差函数,可以看到如果\(ys <\!\!< 1\)则误差函数会得到一个很大的值,即对严重的错分现象施加了比较大的惩罚。但是,由于二次函数抛物线的性质,可以看到如果\(ys >\!\!> 1\),即分类非常正确时,误差函数也会加以很大的惩罚,所以误差函数的表现并不总是尽人意。不过无论如何,如果平方误差小,一定会说明0/1误差小
对于交叉熵误差函数,可以看到它是关于\(ys\)单调递减的。交叉熵误差越小,说明0/1误差越小,反之亦然。
为了推导的方便,可以对交叉熵误差函数做一个缩放(实际上就是换了一个底)。缩放后的交叉熵误差函数修正如下: \[ {\rm err}_{\rm SCE}(s, y) = \log_2(1+\exp(-ys)) \]
修改后的交叉熵误差函数能保证当\(ys=0\)时交叉熵误差函数和0/1误差函数相切,即图像变为下图
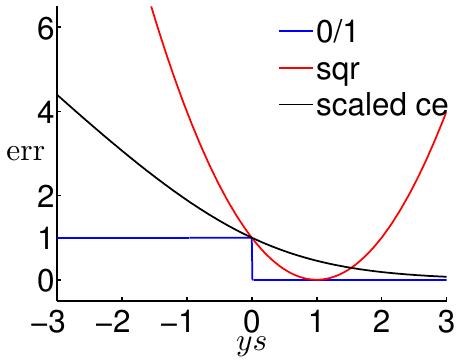
可以看到,换底以后,交叉熵误差函数成为了0/1误差函数严格的上界。也就是说,对任意\(ys\)(其中\(s = {\bf w}^\mathsf{T}{\bf x}\)),有 \[ \begin{align*} &{\rm err}_{0/1}(s, y) \le {\rm err_{SCE}}(s, y) = \frac{1}{\ln 2}{\rm err_{CE}}(s, y) \\ \Longrightarrow & \ \ E_{\rm in}^{0/1}({\bf w}) \le E_{\rm in}^{\rm SCE}({\bf w}) = \frac{1}{\ln 2}E_{\rm in}^{\rm CE}({\bf w}) \\ &\ \ E_{\rm out}^{0/1}({\bf w}) \le E_{\rm out}^{\rm SCE}({\bf w}) = \frac{1}{\ln 2}E_{\rm out}^{\rm CE}({\bf w}) \end{align*} \] 套用之前的VC维理论,有 \[ \begin{align*} E_{\rm out}^{0/1}({\bf w}) &\le E_{\rm in}^{0/1}({\bf w}) + \Omega^{0/1} \\ &\le \frac{1}{\ln 2}E_{\rm in}^{\rm CE}({\bf w}) + \Omega^{0/1} \end{align*} \] 或者从另一个方向,有 \[ \begin{align*} E_{\rm out}^{0/1}({\bf w}) &\le \frac{1}{\ln 2}E_{\rm out}^{\rm CE}({\bf w}) \\ &\le \frac{1}{\ln 2}E_{\rm in}^{\rm CE}({\bf w}) + \frac{1}{\ln 2} \Omega^{CE} \end{align*} \] 无论从哪个方向,都可以得出结论 \[ {\rm small\ }E_{\rm in}^{\rm CE}({\bf w}) \Rightarrow {\rm small\ }E_{\rm out}^{0/1}({\bf w}) \] 平方误差同理。因此,这证明,Logistic回归和线性回归都可以用在线性分类问题上,算法为
- 在\(y_n \in \{-1, +1\}\)的\(\mathcal{D}\)上运行Logistic回归或线性回归算法得到\({\bf w}_{\rm REG}\)
- 返回\(g({\bf x}) = {\rm sign}({\bf w}_{\rm REG}^\mathsf{T}{\bf x})\)
使用线性回归的好处是优化变得容易,但是对\(|ys|\)比较大的情况,其得到的误差比0/1误差宽松太多。使用Logistic回归的好处是优化也比较容易,但是类似于线性回归,它对\(ys <\!\!< 0\)的情况得到了太宽松的上界。另一方面,在数据集线性可分时,PLA非常有效而且效果很强,但是对线性不可分的情况只能使用启发式的口袋算法
在实践中,通常把线性回归得到的权重用来初始化PLA/口袋算法/Logistic回归的\({\bf w}_0\)。另外,大部分人会使用Logistic回归,而少用口袋算法
随机梯度下降
PLA、口袋算法和Logistic回归算法都使用了迭代优化的方法,权重\(\bf w\)会一步步地越变越好。在PLA算法中,每一个错误点的发现都会导致权重的更改,每次迭代的时间复杂度仅为\(O(1)\)。然而,Logistic回归的每次迭代会看输入数据集\(\mathcal{D}\)上的每个点,将所有数据点的梯度算出来,求和以后算出总梯度,再去产生\({\bf w}_{t+1}\)。因此,Logistic回归每次迭代的时间复杂度为\(O(N)\)
有没有可能提高效率,让Logistic回归每次迭代的时间复杂度也变为\(O(1)\)?回顾Logistic回归的迭代方法 \[ {\bf w}_{t+1} \leftarrow {\bf w}_t + \eta \underbrace{\frac{1}{N}\sum_{n=1}^N \theta(-y_n{\bf w}_t^\mathsf{T}{\bf x}_n)(y_n{\bf x}_n)}_{-\nabla E_{\rm in}({\bf w}_t)} \] 要让每次迭代更新的时间复杂度为\(O(1)\),需要同时满足两个要求:首先,方向\(\bf v\)不应该变化太多,还应该有\({\bf v} \approx -\nabla E_{\rm in}({\bf w}_t)\)。这是因为由前面的推导,这个方向梯度的减小是最快的。其次,希望计算\({\bf v}\)时只用到一个点\(({\bf x}_n, y_n)\),因为只有这样才能保证时间复杂度。所以,原式中的求和项一定要想办法去掉
如何去掉这个求和项?注意到式子中有一个\(\frac{1}{N}\sum_{n=1}^N\)。可以很自然地将其与期望\(\mathcal{E}\)的概念联系起来:如果随机且均匀地选取了\(n\)个点求它们梯度的期望,就应该是这样计算。假如每次只随机取一个点,将这个点的梯度看作是梯度的期望,就可以避免求和的过程。这种做法叫做随机梯度下降(SGD),将整体的梯度看作是选出的若干点(“若干”可以为1)梯度的期望,即 \[ \nabla_{\bf w} E_{\rm in}({\bf w}) = \mathcal{E}_{ {\rm random\ }n}\nabla_{\bf w}{\rm err}({\bf w}, {\bf x}_n, y_n) \] SGD的Logistic回归迭代为: \[ {\bf w}_{t+1} \leftarrow {\bf w}_t + \eta \underbrace{\theta(-y_n{\bf w}_t^\mathsf{T}{\bf x}_n)(y_n{\bf x}_n)}_{-\nabla {\rm err}({\bf w}_t, {\bf x}_n, y_n)} \] 可以将随机梯度看作是真实梯度加上了一些期望为0的噪声:虽然总体上还是沿真实梯度方向前进,但是每一步都会向随机的某个方向偏一点。SGD的做法就是把原来算法中真实的梯度换成随机的梯度。由于噪声的期望为0,因此经过足够多的迭代以后,真实梯度的平均也约等于随机梯度的平均。这样的好处是,计算量减小了很多,尤其适合于大数据环境或在线学习的状况。但是,SGD会比较不稳定(尤其是\(\eta\)很大的情况下)
回顾PLA的迭代操作 \[ {\bf w}_{t+1} \leftarrow {\bf w}_t + 1\cdot [\![y_n \not= {\rm sign}({\bf w}_t^\mathsf{T} {\bf x}_n)]\!](y_n{\bf x}_n) \] 跟前面SGD Logistic回归相比,可以把SGD Logistic回归看作是“软化的”PLA:不再非黑即白地根据其对错来更新,而是根据错误程度更新:错得多,更新得多;错得少,更新得也少。反过来看,当\({\bf w}_t^\mathsf{T}{\bf x}_n\)很大时,PLA可以看作是\(\eta = 1\)的SGD Logistic回归
真正使用SGD Logistic回归时,有两条实践经验:
- 停止条件一般是设定迭代次数\(t\)足够大即可
- \(\eta\)一般设置为0.1
使用Logistic回归做多元分类
已有的这些分类算法不仅可以做“判断题”(二元分类),也可以做“选择题”(多元分类)。假设要分的类不再是\(\circ\)和\(\times\)两类,而是\(\square\)、\(\diamond\)、\(\triangle\)和\(\star\)四类,应该怎么做?可以使用线性分类器逐个看样本是否属于这四类,例如,判断样本是否为\(\square\)时,可以划归到所有\(\square\)是\(\circ\),剩下三类都是\(\times\)的情况,以此类推
在大部分情况下,这种方法都能做出不错的选择。但是有两种情况可能需要费一些周章:其一,对某些样本,可能有两个(或以上)分类器都认为它应该属于自己的类别;另一种情况是,对某些样本,可能有两个(或以上)分类器都认为它不应该属于自己的类别
因此,可以使用Logistic回归来“软化”,不再计算每个样本是否属于某个类别,而是计算每个样本属于每个类别的概率。仍然以判断样本是否为\(\square\)时的状况为例,此时还是所有\(\square\)都是\(\circ\),剩下三类样本都是\(\times\),但是这时计算的是\(P({\square}|{\bf x})\),最好的假设函数为 \[ g({\bf x}) = \mathop{ {\rm arg}\max}_{k \in \mathcal{Y}} \theta\left({\bf w}_{[k]}^\mathsf{T}{\bf x}\right) \] 因此多元分类的一种算法如下(笔记注:讲义上写的算法名称叫做OVA(One-Versus-All),但是sklearn包偏爱的称法为OVR(One-Versus-Rest))
对每个\(k \in \mathcal{Y}\)
将数据集转化为如下形式,然后运行Logistic回归算法以获取\({\bf w}_{[k]}\) \[ \mathcal{D}_{[k]} = \{({\bf x}_n, y_n'=2[\![y_n=k]\!] - 1)\}_{n=1}^N \] 返回\(g({\bf x}) = \mathop{ {\rm arg}\max}_{k \in \mathcal{Y}} \theta\left({\bf w}_{[k]}^\mathsf{T}{\bf x}\right)\)
这个方法的好处是很有效(只需要运行\(k\)次),而且可以适用于任何类似于Logistic回归的算法(只要这个算法可以输出概率)。但是如果类别数很多,会导致不平衡类别问题的出现,即正负样本的比例会差得比较多。在这种情况下,所有Logistic回归分类器都倾向于猜\(\times\)(笔记注:实际是给出一个特别小的概率)。尽管也可以在这些小概率中选择最大的概率作为样本所属类别,但是在这种情况下Logistic回归的表现一般不会太好。统计学中还有一种对Logistic回归的扩展,称为multinomial logistic regression,不过这里没有做太多介绍
尽管存在着问题,OVA算法仍然是一种简单但是特别有效的,可适用于多类别分类的基础算法
使用二元分类做多元分类
前面说到,OVA面临的最大问题是,当类别数很多时,问题会变成不平衡样本分类问题。其原因是将每个类别视作正例时,都是所有样本参与分类过程。如果有\(K\)个类,属于每个类的数据量都近似,那么每次分类时正负样本数量比都是\(1 : K-1\)。为了解决这个问题,可以考虑如何在分类时仍然让正负样本数接近1比1。因此,可以使用一对一(OVO, One-Versus-One)的分类法:每次取出\(K\)个类别中属于某两类的样本进行比较,其它样本都不参与分类。这样,总共有\(K \choose 2\)个分类步骤,得到\(K \choose 2\)个分类器。对于任何一条数据,看这\(K \choose 2\)个分类器各自认为它属于哪个类别,最后哪个类别收到的票数多,哪个类别获胜。可以形象地认为,\(K\)个类别就这个数据两两作赛,谁赢的次数多谁就是冠军。因此OVO分类法返回的假设函数为 \[ g({\bf x}) = {\rm tournament\ champion}\ \{ {\bf w}_{[k, \ell]}^\mathsf{T}{\bf x}\} \] 多元分类的OVO算法总体过程如下
对每个类别对\((k, \ell) \in \mathcal{Y} \times \mathcal{Y}\)
在如下数据集上运行线性二元分类器算法,获得\({\bf w}_{[k, \ell]}\) \[ \mathcal{D}_{[k, \ell]} = \{({\bf x}_n, y_n' = 2[\![y_n = k]\!] - 1): y_n =k{\rm\ or\ }y_n=\ell\} \] 返回\(g({\bf x}) = {\rm tournament\ champion}\ \{ {\bf w}_{[k, \ell]}^\mathsf{T}{\bf x}\}\)
这个算法是每次分类过程效率比较高(因为只使用了少量样本)、稳定,而且也可以适用于任何二元分类算法。但是,算法需要更多空间(存储更多的\({\bf w}\)),预测更慢(因为要跑\(K \choose 2\)个分类过程,训练更多
同样,OVO算法仍然是一种简单但是特别有效的,可适用于多类别分类的基础算法
