Logistic回归问题
二元分类问题,由于误差函数的定义,只关注样本是/否属于某个类别,即\(\mathcal{Y} \in \{-1, +1\}\),理想的假设函数的形式也是\(f({\bf x}) = {\rm sign}(P(+1|{\bf x}) - \frac{1}{2}) \in \{-1, +1\}\)
我们还会关心一个类似的问题。以医院中的例子为例,给定一个病人,可能不再只关心ta是否会得心脏病,而是还关注ta得心脏病的概率/风险/可能性(例如80%)。对这样的问题,要关心的是一个落在0到1之间的值。因此这个问题与原来的二元分类问题有所差别,被称作“软二元分类”问题。求解此问题得到的值越高,说明越有可能是\(\circ\),否则越有可能是\(\times\)。再次强调一下,这里的结果不再是非黑即白的二分法,而是一种可能性。此时目标函数会变化成\(f({\bf x}) = P(+1|{\bf x}) \in [0, 1]\)的形式
理想状况下,要解决这样的问题,我们希望能看到给定\({\bf x}\)数据是正例的概率,即类似如下的条目: \[ ({\bf x}_1, y_1') = 0.9 = P(+1|{\bf x}_1) \\ ({\bf x}_2, y_2') = 0.2 = P(+1|{\bf x}_2) \\ \vdots \\ ({\bf x}_N, y_N') = 0.6 = P(+1|{\bf x}_N) \\ \] 这样,只需要让\(g\)在数据上对概率的预测与实际概率差别越小越好。但是实际上,这样的资料是基本上拿不到的,上帝给的概率并不能看到,我们只能看到“是”或“否”,即真实数据是有噪声的版本,如下(尤其看最后一条) \[ ({\bf x}_1, y_1') = 1 = [\![\circ \sim^? P(y|{\bf x}_1)]\!] \\ ({\bf x}_2, y_2') = 0 = [\![\circ \sim^? P(y|{\bf x}_2)]\!] \\ \vdots \\ ({\bf x}_N, y_N') = 0 = [\![\circ \sim^? P(y|{\bf x}_N)]\!] \\ \] 因此,可以收集到的数据跟之前解二元分类时可以拿到的数据是一样的,只不过目标函数不同。因此,需要考察不同的假设函数集合
要确定假设函数的形式,第一件事还是要确定输入的形式和特征是什么。和之前一样,输入仍然可以表示为\({\bf x} = (x_0, x_1, x_2, \ldots, x_d)\)。一种自然的想法是,仍然计算其加权分数,即 \[ s = \sum_{i=0}^d w_ix_i \] 但是值得关注的并不是这个加权分数,而是根据“分数越高概率越高,分数越低概率越低”这个设定以及“最后要得到一个概率值”这个要求,关注如何将结果缩放到[0, 1]这个区间。通常使用Logistic函数(记为\(\theta\) )来将这个分数映射到\([0, 1]\)区间,因此这个问题称为Logistic回归问题,假设也被称为Logistic假设。其形式为 \[ h({\bf x}) = \theta({\bf w}^\mathsf{T}{\bf x}) \] 其中Logistic函数的定义为 \[ \theta(s) = \frac{e^s}{1+e^s} = \frac{1}{1+e^{-s}} \]
Logistic回归误差
Logistic回归和之前提到的线性分类算法和线性回归算法有类似的地方,即对得到的特征都会做一个加权打分的操作。只不过三者在打分完以后做的事情有不同。可以参看下图
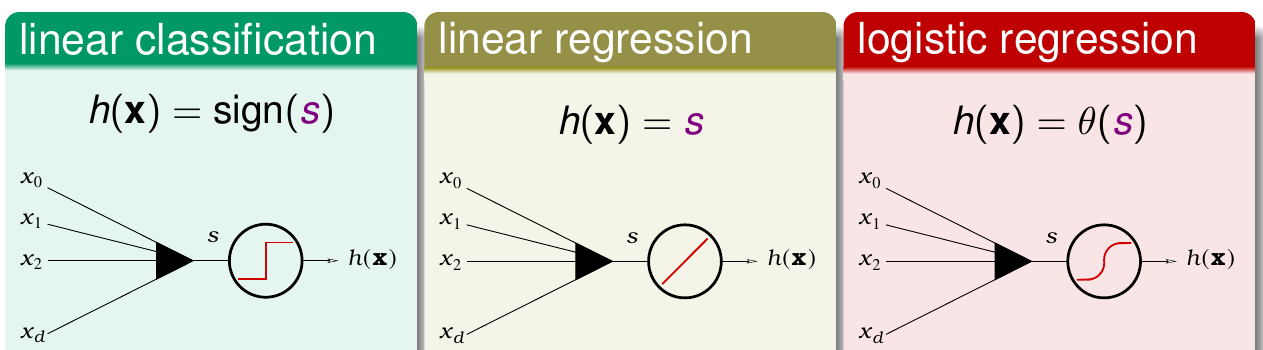
- 对于线性分类问题,算完得分以后,只根据得分的符号来做分类的动作。这里使用的是最简单的误差函数\({\rm err}_{0/1}\)
- 对于线性回归问题,算完得分以后,直接输出得分。误差函数使用平方误差,因为很容易最小化
- 对于Logistic回归问题,算完得分以后,再做一个logistic变换得到最后的结果。那么这里很自然需要关心的问题是,Logistic回归所使用的误差函数是什么?
考虑我们的目标函数为\(f({\bf x}) = P(+1|{\bf x})\),可以稍作变化得到给定\(\bf x\)时\(y\)的概率,即 \[ P(y|{\bf x}) = \begin{cases}f({\bf x}) & {\rm for\ }y=+1 \\ 1-f({\bf x}) & {\rm for\ } y = -1\end{cases} \] 假设现在得到的数据集为 \[ \mathcal{D} = \{({\bf x}_1, \circ), ({\bf x}_2, \times), \ldots, ({\bf x}_N, \times)\} \] 根据前面的设定和贝叶斯定理,可以推出\(\mathcal{D}\)由\(f\)产生的概率,为 \[ P({\bf x}_1)P(\circ | {\bf x}_1) \times P({\bf x}_2)P(\times | {\bf x}_2) \times \ldots \times P({\bf x}_N)P(\times | {\bf x}_N) \] 将上式中的\(P(y|{\bf x})\)换成\(f\),可以得到下面等价的式子 \[ P({\bf x}_1)f({\bf x}_1) \times P({\bf x}_2)(1 - f({\bf x}_2) ) \times \ldots \times P({\bf x}_N)(1 - f({\bf x}_N) ) \] 我们无法直接得到\(f\),但是可以通过学习得到一个假设\(h\),因此可以计算\(h\)生成同样数据集的概率。这个概率一般称之为似然。可以立即得到这个似然值为 \[ P({\bf x}_1)h({\bf x}_1) \times P({\bf x}_2)(1 - h({\bf x}_2) ) \times \ldots \times P({\bf x}_N)(1 - h({\bf x}_N) ) \] 如果有\(h \approx f\),则\(h\)对\(\mathcal{D}\)的似然应该近似于\(f\)产生\(\mathcal{D}\)的概率。而通常\(f\)产生\(\mathcal{D}\)的概率应该非常大,就有 \[ {\rm likelihood}(h) \approx ({\rm probability\ using\ }f) \approx {\rm large} \] 因此可以认为,\(\mathcal{H}\)中最好的\(g\)应该是似然最大的那一个,即 \[ g = \mathop{ {\rm arg}\max}_h {\rm likelihood}(h) \] 又因为logistic函数有对称性,即有 \[ 1 - h({\bf x}) = h(-{\bf x}) \] 因此 \[ {\rm likelihood}( {\rm logistic}\ h) \propto \prod_{n=1}^N h(y_n{\bf x}_n) \] Logistic回归算法的目的就是找到一个\(h\)使得上式最大化。同样由于每个\(h\)都关联一个\({\bf w}\),因此代入\(h\)的定义,目标可以写为 \[ \max_{\bf w} {\rm likelihood}({\bf w}) \propto \prod_{n=1}^N \theta(y_n{\bf w}^\mathsf{T}{\bf x}_n) \] 又因为\(\log (ab) = \log a + \log b\)以及对已有函数取对数不会改变函数的单调性,有 \[ \begin{align*} &\max_{\bf w} \prod_{n=1}^N \theta(y_n{\bf w}^\mathsf{T}{\bf x}_n) \\ \Leftrightarrow &\max_{\bf w} \ln \prod_{n=1}^N \theta(y_n{\bf w}^\mathsf{T}{\bf x}_n) \\ \Leftrightarrow & \max_{\bf w} \sum_{n=1}^N \ln \theta(y_n{\bf w}^\mathsf{T}{\bf x}_n) \\ \Leftrightarrow & \min_{\bf w} \frac{1}{N} \sum_{n=1}^N -\ln \theta(y_n{\bf w}^\mathsf{T}{\bf x}_n) \\ \Leftrightarrow & \min_{\bf w} \frac{1}{N}\sum_{n=1}^N \ln(1 + \exp(-y_n{\bf w}^\mathsf{T}{\bf x}_n))\hspace{3ex}(\rm definition\ of\ logistic\ function) \end{align*} \] 定义 \[ {\rm err}({\bf w}, {\bf x}, y) = \ln(1 + \exp(-y{\bf w}^\mathsf{T}{\bf x})) \] 记为交叉熵误差函数,那么\(\sum_{n=1}^N {\rm err}({\bf w}, {\bf x}_n , y_n)\)就是Logistic回归问题中的\(E_{\rm in}\)
Logistic回归误差的梯度
有了误差函数,接下来的问题自然就是怎么求出最优的\(\bf w\)。经过分析可以发现,交叉熵误差函数也是连续、可微、二次可微的凸函数,因此第一个想法就是试着推导\(\nabla E_{\rm in}(\bf w)\)。求导有如下结果 \[ \begin{align*} \frac{\partial E_{\rm in}(\bf w)}{\partial {\bf w}} &= \frac{1}{N}\sum_{n=1}^N\frac{1}{1+\exp(-y_n{\bf w}^\mathsf{T}{\bf x}_n)} \cdot \exp(-y_n{\bf w}^\mathsf{T}{\bf x}_n) \cdot (-y_n{\bf x}_n) \\ &= \frac{1}{N}\sum_{n=1}^N \theta(-y_n{\bf w}^\mathsf{T}{\bf x}_n)(-y_n{\bf x}_n) \end{align*} \] 接下来试着求解\(\nabla E_{\rm in}({\bf w}) = 0\)。注意梯度是用\(\theta\)加权\(y_n{\bf x}_n\)的,由于梯度是一个求和项,那么如果所有\(\theta\)都是0,那么求和项就会为0。而当每个\(y_n{\bf w}^\mathsf{T}{\bf x}_n \rightarrow +\infty\)时,\(\theta(-y_n{\bf w}^\mathsf{T}{\bf x}_n)\)才会趋近于0。由于此时每个\(y_n{\bf w}^\mathsf{T}{\bf x}_n\)都是一个巨大的正数,因此有之前感知机部分的知识可以得知,每条数据都被正确分类,这意味着数据集\(\mathcal{D}\)是线性可分的。而大部分情况下,这个条件不能满足,这就要求我们要想办法去解这个方程。而这个式子并不是一个线性的式子。实际上\(\nabla E_{\rm in}({\bf w}) = 0\)并没有解析解
所以如何破?回顾之前的PLA算法,它是迭代的,发现算法犯错的时候会修正\(\bf w\)。为了简单起见,可以把“找出使\({\bf w}_t\)犯错的数据\(({\bf x}_{n(t)}, y_{n(t)})\)”这一步和“改正\({\bf w}_t\)这一步合并,连写为 \[ {\bf w}_{t+1} \leftarrow {\bf w}_t + [\![{\rm sign}({\bf w}_t^\mathsf{T}{\bf x}_n) \not= y_n]\!]y_n{\bf x}_n \] 这里其实有两样东西,其一是更新的方向(这里是\([\![{\rm sign}({\bf w}_t^\mathsf{T}{\bf x}_n) \not= y_n]\!]y_n{\bf x}_n\) ),另一是更新的步长(这里就是1,没有在上式写出)。如果在这里要对更新的方向\({\bf v}\)和更新的步长\(\eta\)做出改变,就会得到不同的机器学习算法。这样的算法一般称为迭代优化方法。
梯度下降
迭代优化方法的思想可以如下表示。其中\(\bf v\)代表更新的方向,\(\eta\)代表步长
对\(t = 0, 1, \ldots\) \[ {\bf w}_{t+1} \leftarrow {\bf w}_t + \eta{\bf v} \] 算法终止时,将最后得到的\(\bf w\)返回为\(g\)
PLA里通过修正错误来得到\(\bf v\)。而Logistic回归,前面可以看到,其损失函数是一个光滑的曲线,这能带来什么样的启发?想象将一个球放在山坡的某个地方,它自然会滚下去,到谷底的时候停住,而停住的点就是梯度为0的点。因此,解Logistic回归问题时,所选的\(\bf v\)就是这里球滚下去的方向,其中为了推导的方便,假设\(\bf v\)的长度是1。比较贪心的想法是,希望小球滚下去时每一步的跨越最大(\(E_{\rm in}\)下降最多),往陡的方向滚。假设限制了每一步只能走\(\eta\)这么大,那么问题就化为找到满足下式的\(\bf v\) \[ \min_{|\!|{\bf v}|\!| = 1} E_{\rm in}\underbrace{({\bf w}_t + \eta{\bf v})}_{ {\bf w}_{t+1}} \] 也就是如何找到一个最好的方向。然而这个问题仍然是一个不好解的问题:仍然是要优化一个非线性函数,而且更丧心病狂的是居然还加了一个条件。因此,这个问题并不比\(\min_{\bf w}E_{\rm in}({\bf w})\)好解。考虑到目前学过的容易的问题都跟线性函数有关,有没有办法把上面的式子变成一个关于\(\bf v\)的线性函数?
答案是可以的。任何曲线如果只观察其非常微小的一段,这一段都可以认为是一条长度很短的直线。因此在\(\eta\)特别小时,使用泰勒展开,有 \[ E_{\rm in}({\bf w}_t + \eta{\bf v}) \approx E_{\rm in}({\bf w}_t) + \eta {\bf v}^\mathsf{T}\nabla E_{\rm in}({\bf w}_t) \] 因此问题转化为,当\(\eta\)很小时,求 \[ \min_{|\!|{\bf v}|\!| = 1} E_{\rm in}({\bf w}_t) + \eta {\bf v}^\mathsf{T}\nabla E_{\rm in}({\bf w}_t) \] 由于\(E_{\rm in}\)是常数,因此最好的\(\bf v\)与梯度方向相反就可以。又因为\(\bf v\)是单位向量,因此 \[ {\bf v} = \frac{-\nabla E_{\rm in}({\bf w}_t)}{|\!|\nabla E_{\rm in}({\bf w}_t)|\!|} \] 所以理想的更新方法(称为梯度下降)为 \[ {\bf w}_{t+1} \leftarrow {\bf w}_t - \eta\frac{\nabla E_{\rm in}({\bf w}_t)}{|\!|\nabla E_{\rm in}({\bf w}_t)|\!|} \] 注意这里\(\eta\)不能太小也不能太大。如果\(\eta\)太小,收敛会很慢;如果\(\eta\)太大,曲线的这一小段就不能看作是一段很短的直线,逼近不准,因此收敛不稳定。具体示例可见下图
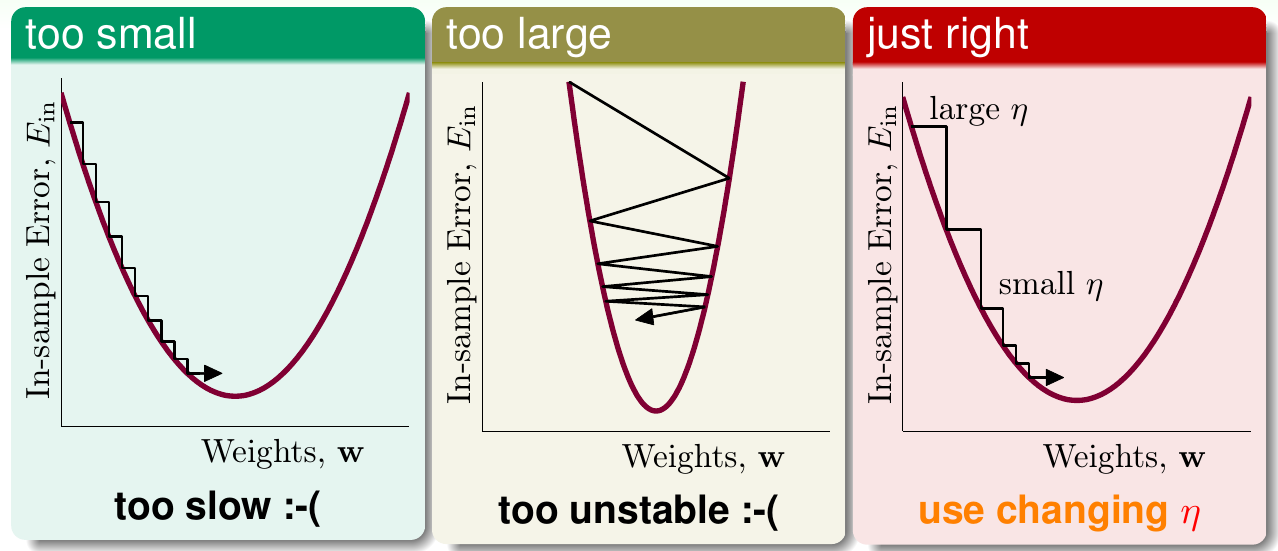
最好的方法是\(\eta\)要经常改变。梯度越大,\(\eta\)越大;梯度越小,\(\eta\)越小,即\(\eta \propto {|\!|\nabla E_{\rm in}({\bf w}_t)|\!|}\)。这个关系也可以表示为\(\eta = \eta_0 \cdot {|\!|\nabla E_{\rm in}({\bf w}_t)|\!|}\),而稍作变换就有\(\eta_0 = \eta / {|\!|\nabla E_{\rm in}({\bf w}_t)|\!|}\)。如果把\(\eta_0\)用一个新的\(\eta\)替换,上式就可以写为 \[ {\bf w}_{t+1} \leftarrow {\bf w}_t - \eta \nabla E_{\rm in}({\bf w}_t) \] 称此时的\(\eta\)为固定的学习率,上式也被称为固定学习率的梯度下降
因此,Logistic回归算法可以表示如下:
初始化\({\bf w}_0\)
当\(t=0,1,\ldots\)时
计算 \[ \nabla E_{\rm in}({\bf w}_t) = \frac{1}{N} \sum_{n=1}^N\theta(-y_n{\bf w}_t^\mathsf{T}{\bf x}_n)(-y_n{\bf x}_n) \] 更新权重 \[ {\bf w}_{t+1} \leftarrow {\bf w}_t - \eta \nabla E_{\rm in}({\bf w}_t) \] 直到\(\nabla E_{\rm in}({\bf w}_{t+1}) = 0\)或迭代次数足够多
将最后得到的\({\bf w}_{t+1}\)返回为\(g\)
可以看到,Logistic回归算法的时间复杂度与口袋算法每次迭代的时间复杂度相似
