NTUML 9. 线性回归

线性回归问题

回顾之前举的银行信用卡问题，如果要关注的问题不再是“给不给发卡”而是“发多大的额度”，那么这就不再是一个二元分类问题，而输出空间已经是实数集（这里实际上是实数集的一个子集）了，因此是一个回归问题。

回归问题的假设函数应该是什么样的？假设已经提取好了$d$个特征$x_1, x_2, \ldots, x_d$，可以像感知机问题那样再加入一个新的常数项$x_0$组成输入向量$\bf x$。一个直观的做法是为每个特征赋予一个权重$w_i$，这样这些特征的加权均值就应该接近于期望得到的$y$，即 \[ y \approx \sum_{i=0}^d w_ix_i \] 这其实就是线性回归的假设函数了，即$h({\bf x}) = {\bf w}^\mathsf{T}{\bf x}$。可以看到这个假设函数跟感知机的有点像，但是不需要取符号，因为最后要得到的结果就应该是个连续值。

要洞悉线性回归的思想，可以从最简单的情况入手。假设输入只有一个维度，平面$\mathbb{R}^2$上的直角坐标系横轴为输入$x$ ，纵轴为输出$y$，那么训练数据就是落在坐标系上的若干个点，而对任意$x \in \mathbb{R}$，假设函数求出来的对应的值$h(x) \in \mathbb{R}$应该连成一条直线。期望是对于训练集里任意的点$x_i$，假设函数值$h(x_i)$应该尽量接近于这个点已知的值$y_i$。那么如何衡量$h(x_i)$和$y_i$的接近程度？一种方法就是计算这两个值之间差的绝对值$|h(x_i) - y(i)|$，称作残差。线性回归的目的就是找到合适的超平面，使得残差尽量小。类似的道理推广到n维空间$\mathbb{R}^n$也是一样的

既然问题求解的目的已经确定，那么对应的误差衡量函数就很明朗。通常情况下，回归问题所使用的误差函数叫做平方误差函数，即 \[ {\rm err}(\hat{y}, y) = (\hat{y} - y)^2 \] 如前面讨论的那样，误差通常会被分为样本内误差和样本外误差。样本内误差被记为 \[ E_{\rm in}(h) = \frac{1}{N}\sum_{n=1}^N(h({\bf x}_n) - y_n)^2 \] 由于有$h({\bf x}_n) = {\bf w}^\mathsf{T}{\bf x}_n$，因此一个$h$通常会对应于一个$\bf w$，$E_{\rm in}$也可以表示为一个关于${\bf w}$的函数。类似地，样本外误差也可以表示为一个关于$\bf w$的函数 \[ E_{\rm out}({\bf w}) = \mathcal{E}_{({\bf x}, y) \sim P}({\bf w}^\mathsf{T}{\bf x} - y)^2 \] 根据之前的课程，接下来要着重解决的问题就是怎么使$E_{\rm in}$尽可能小

线性回归算法

首先可以试着把上一节得到的$E_{\rm in}$用矩阵形式表示，以使得其形式变得更加简洁。 \[ \begin{align*} E_{\rm in}({\bf w}) &= \frac{1}{N}\sum_{n=1}^N({\bf w}^\mathsf{T}{\bf x}_n - y_n)^2 = \frac{1}{N}\sum_{n=1}^N({\bf x}_n^\mathsf{T}{\bf w} - y_n)^2 \\ &=\frac{1}{N} \left|\!\left|\begin{array}{c} {\bf x}_1^\mathsf{T}{\bf w} - y_1 \\ {\bf x}_2^\mathsf{T}{\bf w} - y_2 \\ \cdots \\ {\bf x}_N^\mathsf{T}{\bf w} - y_N \end{array}\right|\!\right|^2 \\ &= \frac{1}{N} \left|\!\left|\left[\begin{array}{c}--{\bf x}_1^\mathsf{T}-- \\ --{\bf x}_2^\mathsf{T}-- \\ \cdots \\ --{\bf x}_N^\mathsf{T}-- \end{array}\right]{\bf w}-\left[\begin{array}{c}y_1 \\ y_2 \\ \cdots \\ y_N\end{array}\right]\right|\!\right|^2 \\ &= \frac{1}{N}|\!|{\rm X}{\bf w} - {\bf y}|\!|^2 \end{align*} \] 最后得到的各矩阵/向量维度为：

${\rm X}$：$N\times (d+1)$
${\bf w}$：$ (d+1) 1$
${\bf y}$：$N \times 1$

由于$E_{\rm in}$中只有${\bf w}$是未知数，而经过证明可以发现，$E_{\rm in}(\bf w)$是连续且可微的凸函数。凸函数的一个重要性之就是，其在极值点的梯度为0，而梯度的定义是把函数在每个方向上做偏微分，因此在极值点梯度的每个分量都是0。即最优的$\bf w_{\rm LIN}$满足$\nabla E_{\rm in}({\bf w}_{\rm LIN}) = {\bf 0}$

将$E_{\rm in}$的表达式展开并由以下两条矩阵求导规则（$\rm A$是矩阵） \[ \begin{align*} \frac{\partial ({\bf x}^\mathsf{T}{\rm A}{\bf x})}{\partial {\bf x}} &= 2{\rm A}{\bf x} \\ \frac{\partial ({\bf x}^\mathsf{T}{\bf a})}{\partial {\bf x}} &= {\bf a} \end{align*} \] 可知 \[ \begin{align*} E_{\rm in}(\bf w) &= \frac{1}{N}|\!|{\rm X}{\bf w} - {\bf y}|\!|^2 = \frac{1}{N}({\rm X}{\bf w} - {\bf y})^\mathsf{T}({\rm X}{\bf w} - {\bf y}) && {\rm definition\ of\ norm}\\ &= \frac{1}{N}({\bf w}^\mathsf{T}{\rm X}^\mathsf{T} - {\bf y}^\mathsf{T})({\rm X}{\bf w} - {\bf y}) && {\rm rule\ of\ transpose}\\ &= \frac{1}{N}({\bf w}^\mathsf{T}{\rm X}^\mathsf{T}{\rm X}{\bf w} - {\bf w}^\mathsf{T}{\rm X}^\mathsf{T}{\bf y} - {\bf y}^\mathsf{T}{\rm X}{\bf w} + {\bf y}^\mathsf{T}{\bf y}) \\ &= \frac{1}{N}({\bf w}^\mathsf{T}{\rm X}^\mathsf{T}{\rm X}{\bf w} - 2{\bf w}^\mathsf{T}{\rm X}^\mathsf{T}{\bf y} + {\bf y}^\mathsf{T}{\bf y}) &&{ {\bf w}^\mathsf{T}{\rm X}^\mathsf{T}{\bf y}}{\rm\ is\ a\ scalar,\ }{a^\mathsf{T} = a}\\ \nabla E_{\rm in}(\bf w) &= \frac{1}{N}(2{\rm X}{\bf w} - 2{\rm X}^\mathsf{T}{\bf y}) = \frac{2}{N}({\rm X}^\mathsf{T}{\rm X}{\bf w} - {\rm X}^\mathsf{T}{\bf y}) \end{align*} \] 将$\nabla_{\rm in}({\bf w})$置为0，如果${\rm X}^\mathsf{T}{\rm X}$是可逆的，那么可以容易解出 \[ {\bf w}_{\rm LIN} = ({\rm X}^\mathsf{T}{\rm X})^{-1}{\rm X}^\mathsf{T}{\bf y} \] 其中$({\rm X}^\mathsf{T}{\rm X})^{-1}{\rm X}^\mathsf{T}$称为$\rm X$的伪逆，记做${\rm X}^\dagger$。由于通常有$N >\!> d + 1$，因此$X^\dagger$通常都会存在

但是有少部分情况有$N < d + 1$，这样会有很多组解。不过即便如此，使用其它定义伪逆矩阵的方法，仍然可以得到其中的一个解有${\bf w}_{\rm LIN} = {\rm X}^\dagger {\bf y}$

实践中如果需要计算${\bf w}_{\rm LIN}$，一般都直接用计算${\rm X}^\dagger$的函数，而不是手动计算$({\rm X}^\mathsf{T}{\rm X})^{-1}{\rm X}^\mathsf{T}$

因此线性回归算法可以定义如下：

1). 从数据集$\mathcal{D}$中构造输入矩阵$\rm X$和输出向量$\bf y$： \[ {\rm X} = \underbrace{\left[\begin{array}{c}--{\bf x}_1^\mathsf{T}-- \\ --{\bf x}_2^\mathsf{T}-- \\ \cdots \\ --{\bf x}_N^\mathsf{T}--\end{array}\right]}_{N \times (d + 1)}\hspace{2ex} {\bf y} =\underbrace{\left[\begin{array}{c}y_1 \\ y_2 \\ \cdots \\ y_N\end{array}\right]}_{N \times 1} \] 2). 计算伪逆$\underbrace{ {\rm X}^\dagger}_{(d+1) \times N}$

3). 计算最优权重$\underbrace{ {\bf w}_{\rm LIN}}_{(d+1) \times 1} = {\rm X}^\dagger {\bf y}$

一般化问题

所以线性回归问题真的是一种机器学习问题，上述的算法真的是一种机器学习算法么？看起来最优权重的值一步就能算出来（这种解称为解析解或者闭合形式解），在计算过程中也没有迭代地减小$E_{\rm in}$和$E_{\rm out}$

实际上，这是一种机器学习算法，因为

它有好的$E_{\rm in}$
变量有限，$E_{\rm out}$是有限的
伪逆的计算过程是迭代的过程，其过程也可以算是在减小$E_{\rm in}$

所谓“黑猫白猫，抓得住老鼠就是好猫”，只要$E_{\rm out}({\bf w}_{\rm LIN})$足够小，这个算法就可以看作是一种好的算法。下面试着证明$\overline{E_{\rm in}}$足够小，但是同样的思想可以用来证明$E_{\rm out}$也足够小

由于$\overline{E_{\rm in}}$是对所有可能数据集$E_{\rm in}$的平均值，而这些数据都来自于相同的分布，因此可以表示为 \[ \overline{E_{\rm in}} = \mathcal{E}_{\mathcal{D} \sim P^N}\{E_{\rm in}({\bf w}_{\rm LIN}{\rm\ w.r.t\ }\mathcal{D})\} \] 其中每个$E_{\rm in}$又可以如下表示 \[ \begin{align*} E_{\rm in}({\bf w}_{\rm LIN}) &= \frac{1}{N}|\!|{\bf y} - \hat{\bf y}|\!|^2 = \frac{1}{N}|\!|{\bf y} -{\rm X}{\bf w}_{\rm LIN}|\!|^2 \\ &= \frac{1}{N}|\!|{\bf y} - {\rm XX}^\dagger{\bf y}|\!|^2 = \frac{1}{N}|\!|({\rm I} - {\rm XX}^\dagger){\bf y}|\!|^2 \end{align*} \] 称${\rm XX}^\dagger$为“帽子矩阵”，记为$\rm H$ ，因为真实值$\bf y$与之相乘会得到预测值$\hat{\bf y}$。帽子矩阵的几何意义可以通过下图解释

该图中，${\bf y} \in \mathbb{R}^N$，而$\hat{\bf y}$是$\rm X$中每个列的线性组合，因此$\hat{\bf y}$属于$\rm X$的列空间。线性回归要让$\bf y$和$\hat{\bf y}$尽可能小，而$\hat{\bf y}$实际上是$\bf y$在$\rm X$列空间（下面简记为$\rm span$ ）中的投影，为了让两者的残差${\bf y}-\hat{\bf y}$尽可能小，即让$\bf y$到$\rm span$的距离最短，因此只能有${\bf y}-\hat{\bf y}$ 垂直于 ${\rm span}$。所以$\rm H$起到的就是投影的作用，将任意向量$\bf y$投影到$\rm X$的列空间中，投影成$\hat{\bf y}$，而${\rm I} - {\rm H}$则是计算残差${\bf y}-\hat{\bf y}$，它有一个很好的性质： \[ {\rm trace}({\rm I}- {\rm H}) = N - (d + 1) \] 这条性质的物理意义在于，自由度为$N$的向量被投影到$d+1$维空间以后，残差的自由度最多只有$N-(d+1)$。证明如下（简记$\rm trace$为$\rm tr$，并记${\rm I}_d$是$d$维单位矩阵）： \[ \begin{align*} {\rm tr(I-H)} &= {\rm tr(I}_n) - {\rm tr(H)} && {\rm tr(A+B) = tr(A) + tr(B)} \\ &= N- {\rm tr(H)} \\ {\rm tr(H)} &= {\rm tr(XX}^\dagger) \\ &= {\rm tr(X(X^\mathsf{T}X)^{-1}X^\mathsf{T})} && {\rm definition\ of\ X}^\dagger \\ &= {\rm tr((X^\mathsf{T}X)^{-1}X^\mathsf{T}X)} && {\rm tr(AB) = tr(BA)} \\ &= {\rm tr(I}_{d+1}) \\ &= d+1 \\ \therefore {\rm tr(I-H)} &= N- (d+1) \hspace{3ex} \blacksquare \end{align*} \] 对$\bf y$引入误差，情况会略有变化，见下图

假设现在有一个理想的目标函数$f$，那么$f({\rm X})$肯定会落在$\rm X$的列空间中。现在，可以把观察到的$\bf y$看作是理想目标函数值与噪声的加和，即${\bf y} = f({\rm X}) + {\rm noise}$。由于要考察的残差仍然是${\bf y} - \hat{\bf y}$，因此这个残差可以看作是噪声经过矩阵$\rm I-H$的转换，即$E_{\rm in}$就是把$\rm I-H$用在噪声上。将这个关系代入到残差的表达式中，有： \[ \begin{align*} E_{\rm in}({\bf w}_{\rm LIN}) = \frac{1}{N} |\!|{\bf y} - \hat{\bf y}|\!|^2 &= \frac{1}{N}|\!|{\rm (I-H)noise}|\!|^2 \\ &= \frac{1}{N}(N-(d+1))|\!|{\rm noise}|\!|^2 \end{align*} \] 因此可以得到$E_{\rm in}$和$E_{\rm out}$的均值（不过后者的计算更加复杂） \[ \begin{align*} \overline{E_{\rm in}} = {\rm noise\ level} \cdot \left(1 - \frac{d+1}{N}\right) \\ \overline{E_{\rm out}} = {\rm noise\ level} \cdot \left(1 + \frac{d+1}{N}\right) \end{align*} \] 哲学上的意义是，噪声的存在使得模型的学习过程中也对噪声数据进行了学习，学到的$\bf w$可能偏向了某个方向。由于测试数据是新鲜的，没看到过的，没用在学习过程中的数据，因此此消彼长，误差对偏向的方向惩罚更多。这样可以得到一个学习曲线图

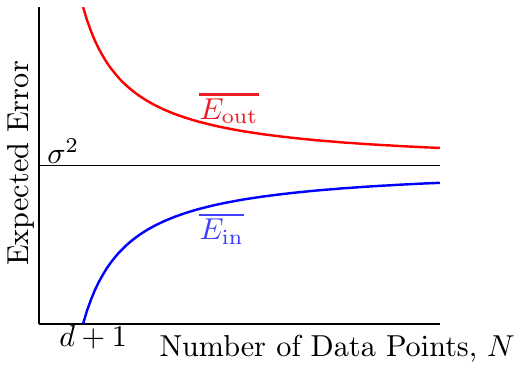
可以看到，随着样本数量$N$的增大，$E_{\rm in}$增大，$E_{\rm out}$减小。但是最后随着$N \rightarrow \infty$，两者都会收敛到$\sigma^2$，即noise level。因此一般化误差（即$E_{\rm in}$与$E_{\rm out}$平均情况下相差多少）为$\frac{2(d+1)}{N}$

综上所述，当$N$尽可能大，噪声不影响时，学习是已经发生了的

用于二元分类的线性回归

考虑之前提到的线性分类问题，已经被证明是NP难的。而线性回归却有非常有效的解析解可以一步得出结果。既然分类问题的结果$\{-1, +1\} \in \mathbb{R}$，也在线性回归的解空间里，那么可不可以用线性回归的思想求解分类问题呢？有人提出了一种做法：

在数据集$\mathcal{D}$上运行线性回归算法，求出${\bf w}_{\rm LIN}$
返回$g({\bf x}) = {\rm sign}({\bf w}_{\rm LIN}^\mathsf{T}{\bf x})$

如何说明这个做法是可行的呢？注意两个问题最大的区别是两者的误差函数定义不同：

0/1分类问题的损失函数为${\rm err}_{0/1} = [\![{\rm sign}({\bf w}^\mathsf{T}{\bf x}) \not= y]\!]$
回归问题的损失函数为最小平方误差${\rm err_{sqr}} = \left({\bf w}^\mathsf{T}{\bf x} - y\right)^2$

可以画出两个函数的曲线（横轴为${\bf w}^\mathsf{T}{\bf x}$，纵轴为$\rm err$），分情况讨论（期望$y=1$还是$y=-1$）

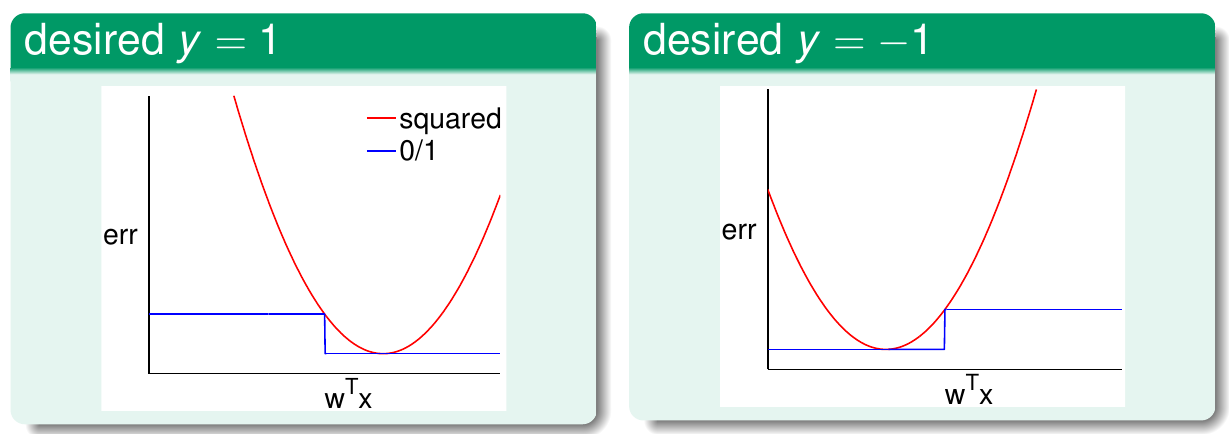
0/1误差函数与最小平方误差函数的图像比较。左为期望样本为正例的情况，右为期望样本为负例的情况

先看左边数据为正例的情况。由于此时数据为正例，因此其标签为1。最小平方误差函数以${\bf w}^\mathsf{T}{\bf x}$为自变量时，函数图像是一个抛物线，在${\bf w}^\mathsf{T}{\bf x} = y = 1$时取得最低点0。此时0/1分类误差函数也取得0，因为此时${\bf w}^\mathsf{T}{\bf x}$的符号与$y$相同，不等号不成立，因此两函数交于$(1, 0)$点。此外，当${\bf w}^\mathsf{T}{\bf x} = 0$时，该点正好处在0/1分类误差函数变化的阶梯点上。但是由于${\bf w}^\mathsf{T}{\bf x}$的符号跟$y$的符号不一致，因此0/1误差函数取1。而最小平方差函数在此时的值也为1（$(0-1)^2 = 1$），因此两函数还交于$(0, 1)$点。画出所有图像以后，可以发现在$\mathbb{R}$上总有${\rm err}_{\rm sqrt} \ge {\rm err}_{0/1}$。同样的结论也可以用在右边数据为负例的情况。因此，由VC维的理论可以有 \[ \begin{align*} {\rm classification\ }E_{\rm out}({\bf w}) &\le {\rm classification\ }E_{\rm in}({\bf w}) + \sqrt{\cdots\cdots} \\ & \le {\rm regression\ }E_{\rm in}({\bf w}) + \sqrt{\cdots\cdots} \end{align*} \] 即回归问题的样本内误差加上一个常量，可以是分类问题样本外误差的一个上界。所以最优化的${\bf w}_{\rm LIN}$也可以解决分类问题。实践中，${\bf w}_{\rm LIN}$是一个不错的基线分类器，也可以用来做PLA算法或口袋算法的初始权重