序言
按照布隆菲尔德的理论,词被认为是人类语言中能自行独立存在的最小单位,是“最小自由形式”。因此,对西方语言做NLP时,以词为基石是一个很自然的想法(甚至对于汉语这种没有明显词界限的语言来说,分词也成为了一个重要的工作)
但是,将某个语言的词穷举出来是不太现实的。首先,名词、动词、形容词、副词这四种属于开放词类,总会有新的词加入进来。其次,网络用语会创造出更多新词,或者为某个词给出不规则的变形。最后,以德语为代表的语言通常会将几个基本词组合起来,形成一个复合词,例如Abwasserbehandlungsanlage “污水处理厂”可以被细分为Abwasser、behandlungs和Anlage三个部分。韩语、日语等黏着语里这种现象更加明显(需要说明的是,尽管德语里存在着这种黏着语构词的方法,但是传统意义上不把德语看作是黏着语的一种)。即便是存在某个语言能获得其完整词表,词表的数量也会非常庞大,使得模型复杂度很高,训练起来很难。对于以德语、西班牙语、俄语为代表的屈折语,也会存在类似的问题(例如西班牙语动词可能有80种变化)。因此,在机器翻译等任务中,从训练语料构造词表时,通常会过滤掉出现频率很低的单词,并将这些单词统一标记为UNK。根据Zipf定律,这种做法能筛掉很多不常见词,简化模型结构,而且可以起到部分防止过拟合的作用。此外,模型上线做推断时,也有很大概率会遇到在训练语料里没见过的词,这些词也会被标为UNK。所有不在词表里被标记为UNK的词,通常被称作集外词(OOV)或者未登录词
对未登录词的处理是机器翻译领域里一个十分重要的问题。[sennrich2016]认为,对于某些未登录词的翻译可能是”透明“的,包括
- 命名实体,例如人名、地名等。对于这些词,如果目标语言和源语言的字母体系相同,可能可以直接抄写;如果不同,需要做些转写。例如将英语的Barack Obama转写成俄语的Барак Обама
- 借词,可以通过字母级别的翻译做到,例如将claustrophobia翻译成德语的Klaustrophobie和俄语的Клаустрофобия
- 词素复杂的词,例如通过组合或者屈折变化得到的词,可以将其进一步拆分为词素,通过分别翻译各个词素的得到结果。例如将英语的solar system翻译成德语的Sonnensystem或者匈牙利语的Naprendszer
因此,将词拆分为更细粒度的subword,可以有助于机器翻译效果的提升。文章同时指出使用一种称为“比特对编码”(Byte Pair Encoding——BPE)的算法可以将词进一步划分,但是BPE对单词的划分是纯基于统计的,得到的subword所蕴含的词素,或者说形态学信息,并不明显。因此,本文对一种基于形态学的分词器Morfessor也做了一个介绍。Morfessor使用的是无监督学习的方法,能达到不错的准确率。最后,本文会重点介绍2016年FAIR提出的一种基于subword的词嵌入表示方法fastText
除去subword方法以外,还可以将词拆成字符,为每个字符训练一个字符向量。这种方法很直观,也很有效,不过无需太费笔墨来描述。关于字符向量的优秀工作,可以参考[Bojanowski2015]的“相关工作”部分。
分词方法介绍
BPE
原理与算法
BPE算法[gage1994]的本质实际上是一种数据压缩算法。数据压缩的一般做法都是将常见比特串替换为更短的表示方法,而BPE也不例外。更具体地说,BPE是找出最常出现的相邻字节对,将其替换成一个在原始数据里没有出现的字节,一直循环下去,直到找不到最常出现的字节对或者所有字节都用光了为止。打包数据之前,算法会写出字节对的替换表。例如,对"lwlwlwlwrr"使用BPE算法,会先把lw替换为a,得到"aaaarr",然后把"aa"替换为"b",得到"bbrr"。此时所有相邻字节对"bb"、"br"、"rr"的出现次数相等,迭代结束,输出替换表{"b" -> "aa", "a" -> "lw"}
对于压缩算法而言,这种做法还不够,需要考虑更多细节。但是对于分词而言,上述流程已经足够了(实际上,真正使用时也没有什么替换表之类的)。将BPE用作分词时,先将词表里的所有单词展开成字符序列,并在末尾加一个特殊标记</w>,以恢复成原有的标识符。然后,也是对所有字符对做计数,找到出现最频繁的(例如("A", "B")),将其合并得到新的符号"AB",看做一个“字符”,如此往复。因此,最后词表大小是原始词表大小+合并操作的次数。为了效率起见,BPE不考虑跨词的字符组合。BPE算法的核心学习过程可以写做如下Python代码
1 | import re |
测试阶段,对未登录词,可以将其先拆分成字符序列,然后用前面学到的组合方式将字符组成更大的,已知的符号。核心算法如下:
1 | def encode(word, bpe_codes): |
由于未登录词通常会被这种方法拆成若干个subword,因此通常会向不在原来词尾的subword后面写明一个分隔符,通常是@@。例如,假如said这个词不在词表里,encode以后得到('sa', 'i', 'd'),那么输出会是sa@@ i@@ d。
使用
可以用命令pip install subword-nmt安装包subword-nmt以后,可以使用如下代码得到BPE的分词结果,以及将BPE的分词方法用到测试语料上
1 | from subword_nmt import apply_bpe, learn_bpe |
Morfessor
BPE是一套很经典也很常用的获取subword的方法,但是美中不足的是该方法完全基于频率统计,因此分出来的subword可能不太包含语法含义。可以考虑将词从语法角度做进一步划分,拆成语素。由于语素是最小的语法单位,是最小的语音语义结合体,因此它们本身比字符承载了更多的语法含义,同时比词更灵活。很多工作,例如[botha2014] [cui2015] [luong2013] [qiu2014]都采取了这样的思路,这些工作在划分语素时都使用了Morfessor [creutz2007] 这个工具,因此本节主要讨论Morfessor的原理。本文主要遵从2.0版本文档[virpioja2013]的脉络,而非原始论文,因此这里主要讨论Morfessor Baseline的2.0实现,没有涵盖Morfessor Categories-MAP的内容。
术语
原文提了三个基本概念,分别是compounds, constructions和atoms。考虑到这三个词比较抽象,不太好找到中文里对应的词,本文所关注的又只是词语划分到词素的过程,因此下文使用的是原文里提供的对应关系:
- compounds,对应于原始词
- constructions,对应于划分得到的词素
- atoms,对应于字母
需要注意的是,Morfessor能做的不只是将词划分为词素,还可以从句子中得到短语,所以compounds等概念在别的任务中,会有不同的具体含义
方法
所有Morfessor的模型包括两个部分,有词典(lexicon)和语法(grammar)。前者存储词素的属性,后者确定如何将词素组成词。Morfessor有两个基本假设
- 词由一个或多个词素构成,单个词中所含词素的上限是该词包含的字母个数
- 组成词的词素是独立出现的。这个假设虽然与事实相悖而且是可能的改进点,但是会使算法变得简单
模型的损失函数来自于对模型的最大后验概率估计(MAP估计),分为两个部分:模型似然(来自于前面的基本假设)和先验概率(决定模型中词典的概率)。训练算法总体上来讲是使用贪婪算法和局部搜索策略,而解码使用了维特比(Viterbi)算法
模型与损失函数
Morfessor使用的是生成概率模型,对给定的参数\(\boldsymbol{\theta}\),产生词\(W\)和分解结果\(A\)(原文称为analysis)。对词\(w\),其分解结果\(\boldsymbol{a}\)可以通过分词函数\(\phi\)获得 \[ \boldsymbol{a} = \phi(w;\boldsymbol{\theta}) \] 此时\(\boldsymbol{a}\)可以看作是一串词素组成的序列\(\boldsymbol{a} = (m_1, \cdots, m_n)\)。\(w\)可以通过对\(\boldsymbol{a}\)做合词操作\(\phi^{-1}\)重新获得。一般情况下,\(\phi^{-1}\)只是一个简单的连接操作,不需要模型
模型的目标是要对观察到的训练数据\(\boldsymbol{D}_W\)寻找最可能的参数\(\boldsymbol{\theta}\): \[ \boldsymbol{\theta}_{\rm MAP} = \mathop{ {\rm arg}\max}_{\boldsymbol{\theta}} p(\boldsymbol{\theta}|\boldsymbol{D}_W) = \mathop{ {\rm arg}\max}_{\boldsymbol{\theta}} p(\boldsymbol{\theta})p(\boldsymbol{D}_W|\boldsymbol{\theta}) \]
似然
假设\(\boldsymbol{D}_W\) 是训练数据,包含\(N\)个单词和单词之间的分界(\(\#w\))。假设每个词出现的概率是独立的,则对数似然为 \[ \begin{align*} \log p(\boldsymbol{D}_W|\boldsymbol{\theta}) &= \sum_{j=1}^N \log p(W=w_j|\boldsymbol{\theta}) \\ &= \sum_{j=1}^N \log \sum_{\boldsymbol{a} \in \Phi(w_j)} p(A=\boldsymbol{a}|\boldsymbol{\theta}) \end{align*} \] 其中\(\Phi(w) = \{\boldsymbol{a} : \phi^{-1}(\boldsymbol{a}) = w\}\)。假设变量\(\boldsymbol{Y}\)为训练数据中的每个单词\(w_j\)分配一个\(\Phi(w_j)\)中的分词序列,即\(\boldsymbol{Y}= (\boldsymbol{y}_1, \cdots, \boldsymbol{y}_N)\),则目标函数变为 \[ \log p(\boldsymbol{D}_W|\boldsymbol{\theta}, \boldsymbol{Y}) = \sum_{j=1}^N \log p(\boldsymbol{y}_j|\boldsymbol{\theta}) = \sum_{j=1}^N \log p(m_{j1}, \cdots, m_{j|\boldsymbol{y}_j|}, \#_w|\boldsymbol{\theta}) \] 由前面的基本假设2,上式可以简化为 \[ \log p(\boldsymbol{D}_W|\boldsymbol{\theta},\boldsymbol{Y}) = \sum_{j=1}^N \left(\log p(\#_w|\boldsymbol{\theta}) + \sum_{i=1}^{|\boldsymbol{y}_j|}\log p(m_{ji}|\boldsymbol{\theta})\right) \]
先验
原始的Morfessor实现将模型参数分为两部分,就是前面说的词典\(\mathcal{L}\)和语法\(\mathcal{G}\)。本文介绍的Morfessor Baseline没有语法参数,所以参数先验\(p(\boldsymbol{\theta}) = p(\mathcal{L})\)。先验概率影响的结果是,对于某个词典,它存储的词素越短越少,则概率越高。对于词素\(m_i\),如果\(p(m_i|\boldsymbol{\theta}) > 0\),那么说它是被存储了的。有\(\mu\)个词素的词典的概率是 \[ p(\mathcal{L}) = p(\mu) \times p({\rm properties}(m_1), \ldots, {\rm properties}(m_\mu)) \times \mu ! \] 使用阶乘项的原因是\(\mu\)个词素有\(\mu !\)种排列方式,而对词典来说相同内容的不同排列都是等价的。\(p(\mu)\)可以忽略掉
上式中的“属性”properties可以进一步划分为“形式”form和用法usage
“形式”指的是词素由哪些字母组成,被认为是独立的。词素\(m_i\)的“形式”的概率分为两个部分,一个是长度分布\(p(L)\),一个是字母序列\(\boldsymbol{\sigma}_i\)的类别分布\(p(C)\) \[ p(\boldsymbol{\sigma}_i) = p(L=|\boldsymbol{\sigma}_i|)\prod_{j=1}^{|\boldsymbol{\sigma}_i|}p(C=\boldsymbol{\sigma}_{ij}) \]
“用法”指的是每个词素的数量\(\tau_i\),\(\nu = \sum_i \tau_i\)是所有词素的总数。可以通过\(\nu\)来计算每个词素的最大似然估计:\(p(m_i|\boldsymbol{\theta}) = \tau_i / (N+\nu)\)。给定\(\mu\)和\(\nu\),词素数量的先验为 \[ p(\tau_1, \ldots, \tau_\mu | \mu, \nu) = 1/{\nu-1 \choose \mu-1} \] 也就是说,每个词素序列的先验都相同
训练与解码算法
Morfessor使用了无监督/半监督学习方法来训练模型,支持批量训练和在线训练。批量训练可以使用全局搜索算法和局部搜索算法,而在线训练只能使用局部搜索算法
参数初始化
Morfessor 2.0的初始化方法是对每个单词的字母之间随机插入空格,将得到的词素放入词典,并对应地初始化\(\boldsymbol{Y}\)
全局维特比算法
Morfessor没有使用HMM常用的前向-后向算法来求解,主要是因为可能的划分方式太多,计算量太大,而且没有封闭解析解。因此工具首先为每个单词找到最可能的分解结果\(\phi_{\rm best}(w;\boldsymbol{\theta}^{(t-1)})\),然后更新参数来最小化损失函数 \[ \boldsymbol{\theta}^{(t)} = \mathop{ {\rm arg}\min}_{\boldsymbol{\theta}}\left\{-\log p(\boldsymbol{\theta}) - \log \prod_{j=1}^{|\boldsymbol{D}_W|}p\left(\phi_{\rm best}(w_j;\boldsymbol{\theta}^{(t-1)})|\boldsymbol{\theta}\right)\right\} \] 这里 \[ \phi_{\rm best}(w;\boldsymbol{\theta}) = \mathop{ {\rm arg}\max}_{\boldsymbol{a}}p(\boldsymbol{a}|w,\boldsymbol{\theta}) = \mathop{ {\rm arg}\max}_{m1,\ldots,m_n: \\ w=m1\ldots m_n}p(m_1,\ldots,m_n,\#_w|\boldsymbol{\theta}) \] 可以进一步使用HMM的维特比算法求解,这里可观察序列是组成单词w的字母序列,隐藏状态是单词的词素。与传统维特比算法的不同在于,一个状态(即一个词素)可以覆盖多个观察值(多个字母)。选出到第\(i\)个观察值的最优路径时,这条路径可能来自于第一到第\(i-1\)个观察值中的任意一个,因此算法时间复杂度是\(O(|w|^2)\)
维特比算法的最大问题是,对于未在之前词典中出现的词素,算法总会把它的概率置为0。由于词素词典总是在缩小的,因此初始化对结果的影响很大。维特比算法也被用来对新词划分词素
此外,全局维特比算法还被Morfessor用作分词算法。Morfessor还支持n-best维特比解码
局部维特比算法
也可以使用在线算法一次处理一条数据,此时对给定单词先得出最优分词方式\(\phi_{\rm best}\),再根据分词结果更新参数。为了处理非零概率问题,需要加入一些平滑手段。设平滑参数为\(\lambda > 0\),则已经存在的词素概率估计为 \[ p_{\rm old}(m_i|\boldsymbol{\theta}) = \frac{\tau_i + \lambda}{\nu + \lambda \mu} \] 没有在词典里的词素概率为 \[ p_{\rm new}(m|\boldsymbol{\theta}) \approx \frac{\lambda}{\nu + \lambda \mu}\times \frac{p(\tilde{\boldsymbol{\theta}})p(\boldsymbol{D}_W|\tilde{\boldsymbol{\theta}})}{p(\boldsymbol{\theta})p(\boldsymbol{D}_W|\boldsymbol{\theta})} \] 其中\(p(\tilde{\boldsymbol{\theta}})\)和\(p(\boldsymbol{D}_W|\tilde{\boldsymbol{\theta}})\)是\(m\)加入到词典里以后得到的近似先验概率和似然概率。假设在训练数据里没有见到过专有名词Matthew,那么标准维特比算法会倾向将其拆分成几个很小的词素。如果\(p_{\rm new}({\rm Matthew}|\boldsymbol{\theta})\)高于分词的似然,那么这个词就会被整体保留。注意平滑维特比算法尽管能引入新的词素,但总体而言它还是一种保守的算法
递归算法
Morfessor Baseline所使用的标准训练算法是一种递归的、贪婪的搜索方法,每一步只考虑修改一小部分参数,选取的修改方法代价最小。递归算法每次只考虑一个可能的单词分解方式\(\boldsymbol{y}_j \in \Phi(w_j)\),将大部分可能的词素的概率设为0,不将它们存进词典,因此不太耗费内存
最简单的情况下,优化算法每次只看一个单词\(w_j\),使用参数找到最小化损失函数的分词序列 \[ \boldsymbol{y}_j^{(t)} = \mathop{ {\rm arg}\min}_{ \boldsymbol{y}_j \in \mathcal{Y}_j}\left\{\min_{\boldsymbol{\theta}} L(\boldsymbol{\theta}, \boldsymbol{Y}^{(t-1)}, \boldsymbol{D}_W)\right\} \] 然后更新参数 \[ \boldsymbol{\theta}^{(t)} = \mathop{ {\rm arg}\min}_{\boldsymbol{\theta}}\left\{L(\boldsymbol{\theta}, \boldsymbol{Y}^{(t)}, \boldsymbol{D}_W)\right\} \] 这两部都会减小损失函数,因此算法最后肯定会收敛到某个局部极小值
由于一个单词的分词结果是上下文无关的,因此可以把\(\boldsymbol{Y}\)存储在一个二分DAG中,叶子节点是词素,其它节点称为“虚拟词素”。顶层节点总是单词
图中的每个节点存储两个数:根节点数量和总数量。前者说明该节点作为单词出现了多少次,后者给出指向该节点的引用数量。对任意节点,该节点的“总数量”是其根节点数量与其直接祖先“总数量”的加和。叶子节点的“总数量”则说明该词素在训练数据中出现了多少次(\(\tau_i\))
递归搜索时,每次局部优化都会修改图的节点,考虑所有将该节点分成两个词素的分法(以及不划分的情况)。如果节点最后被划分,就递归在其孩子节点中搜索。下图给出了算法的逻辑

实践过程中可以通过图中的词素数同时更新图\(\boldsymbol{Y}\)和参数\(\boldsymbol{\theta}\)。如果词素数超过0,就将其加入词典,否则从词典中删除。此外,由于似然的计算很频繁也很耗时,因此每当图的内容变化时都会实时计算对数似然中重要的那部分。继续使用前面的记号,\(N\)为单词总数,\(\mu\)为词表大小,\(\nu\)为词素总数,\(\tau_i\)为词素\(m_i\)的数量,有 \[ \begin{align*} \log p(\boldsymbol{D}_W|\boldsymbol{\theta},\boldsymbol{Y}) &= \sum_{i=1}^\mu \tau_i\log\frac{\tau_i}{N+\nu} + N\log \frac{N}{N+\nu} \\ &= \sum_{i=1}^\mu \tau_i(\log \tau_i -\log(N+\nu)) + N(\log N - \log(N+\nu)) \\ &= \sum_{i=1}^\mu \tau_i \log \tau_i - \sum_{i=1}^\mu \tau_i \log(N+\nu) + N\log N - N \log (N+\nu) \\ &= \sum_{i=1}^\mu \tau_i \log \tau_i + N\log N - (N+\nu)\log (N+\nu) \end{align*} \] 因此只需要实时更新第一项和\(\nu\),就能快速算出对数似然
由于算法的递归性质,它会经常检测一些频繁出现的词素。由于常见单词和词素的划分方式通常不会频繁变化,因此可以统计每个虚拟词素被检验过了多少次,对被检验太多的词素,以一定的概率跳过递归搜索,提高效率。令\(s(w)\)是\(w\)被搜索过的次数,则跳过该词的概率设置为 \[ p({\rm skip}|w) = 1 - \frac{1}{\max(1,s(w))} \] 为了避免其对优化造成影响,\(s(w)\)会被定期更新。全局搜索一般是每个training epoch以后重置一次\(s(w)\),局部搜索则是设置一个迭代样本数量,通常是10000
似然权重与半监督学习
可以通过为似然项加一个权重参数\(\alpha > 0\)来控制模型是倾向将单词分词还是不分 \[ L(\boldsymbol{\theta}, \boldsymbol{D}_W) = -\log p(\boldsymbol{\theta}) - \alpha \log p(\boldsymbol{D}_W|\boldsymbol{\theta}) \] 小的\(\alpha\)使模型尽量细分单词,而大的倾向于保留完整词
fastText
前面介绍的方法主要是如何将词进一步拆分的方法,而fastText(GitHub)本质上并非一种分词方法,它的目的还是要给出每个单词的词向量,只不过在学习词向量的过程中用到了一些subword的信息。这样,对于未登录词,fastText也可以给出一个比较合理的向量表示,而不是用一个统一的unk词向量
fastText可以看作是在word2vec/GloVe之后,ElMo之前最主流,效果最好的词向量训练方法,其最大的改进就是使用了subword来做辅助训练。在fastText提出之前,有很多工作也曾试图向词向量中加入subword信息(更准确地说,主要是加入词素信息),例如[botha2014] [cui2015] [luong2013] [qiu2014]等。不过这些工作,如前面所述,都需要一个分词器来给出词素信息(更多工作介绍,可以参看[bojanowski2017]的“相关工作”部分),因此并没有得到特别广泛的应用
算法原理
fastText继承了word2vec里skip-gram的思想,不过引入了一些subword信息。与原始skip-gram不同的是,fastText对每个给定的输入只预测一个输出。训练时使用了负采样的思想:对窗口内的单词,将其认定为正样本,否则认定为负样本。因此,对位置为\(t\)的输入,假设上下文单词的位置为c,可以得到如下负对数似然 \[
\log \left(1+e^{-s(w_t, w_c)}\right) + \sum_{n \in \mathcal{N}_{t,c}}\log\left(1+e^{s(w_t,n)}\right)
\] 这里\(\mathcal{N}_{t,c}\)是从词表中抽样得到的负样本,\(s\)是一个打分函数,在后文介绍。假设输入是一个有\(T\)个单词的单词序列,对单词\(w_t\)其上下文单词构成的集合为\(\mathcal{C}_t\),logistic损失函数\(\ell\ :\ x \mapsto \log(1+e^{-x})\),则目标函数为 \[
\sum_{t=1}^T \left[\sum_{c\in \mathcal{C}_t} \ell(s(w_t, w_c)) + \sum_{n\in \mathcal{N}_{t,c}} \ell (-s(w_t, n))\right]
\] 如前文所述,fastText并没有只将单词看作是一个整体,而是将每个单词看作是一个包含了若干n元字符的“字组袋”(这个字组袋同时包含了单词本身),并引入分界符<和>。例如,对于单词where,令n=3,则该单词被表示为{<wh, whe, her, ere, re>, <where>}。注意由于分界符的存在,单词her与这里的三元字组her的表示方法不同,前者会被表示为<her>。实践中,fastText提取了所有3、4、5、6元字组
假设包含了所有n-gram的词典大小为\(G\),对于给定单词\(w\),记\(\mathcal{G}_w \subset \{1,\ldots, G\}\)是出现在\(w\)中的n-gram,每个n-gram有一个向量表示\(\boldsymbol{z}_g\),则前面提到的打分函数为 \[ s(w,c) = \sum_{g\in \mathcal{G}_w} \boldsymbol{z}_g^\mathsf{T}\boldsymbol{v}_c \] 对比原始skip-gram的打分函数\(s(w_t, w_c) = \boldsymbol{u}_{w_t}^\mathsf{T}\boldsymbol{v}_{w_c}\),可以看出fastText虽然保留了单词的输出向量,但是单词的输入向量不再是一个单个向量,而是组成它的若干n-gram向量(包括一个自身向量)的加和。这种做法可以共享不同词间相同字组的表示,因此可以为罕见词学到比较可靠的向量
为了减小内存使用量,fastText使用Fowler-Noll-Vo哈希函数(确切说是FNV-1a变体)将字符序列映射到一个1到\(2\times 10^6\)的整数,每个单词由其在字典中的索引号和所包含字组的哈希值集合共同表示
对于未登录词,fastText将组成它的所有n-gram字组向量求和,得出该词的向量表示
实现
fastText使用了梯度下降来求解最优化问题,学习率线性递减。假设训练集有\(T\)个单词,训练过程在整个训练集上迭代\(P\)次,则在时刻\(t\)的学习率为\(\gamma_0 (1-\frac{t}{TP})\),其中\(\gamma_0\)是一个固定的超参数。词向量维度设为300,对每个正样本随机采样5个负样本,随机概率正比于单词出现频率的平方根。窗口大小\(c\)是一个随机变量,来自于1到5的均匀分布。使用的训练集是wiki数据集
参考文献
[sennrich2016] Sennrich, R., Haddow, B., & Birch, A. (2016). Neural Machine Translation of Rare Words with Subword Units. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers) (ACL) (Vol. 1, pp. 1715-1725).
[gage1994] Gage, P. (1994). A New Algorithm for Data Compression. In C User Journal
[botha2014] Botha, J., & Blunsom, P. (2014, January). Compositional morphology for word representations and language modelling. In International Conference on Machine Learning (ICML) (pp. 1899-1907).
[cui2015] Cui, Q., Gao, B., Bian, J., Qiu, S., Dai, H., & Liu, T. Y. (2015). Knet: A general framework for learning word embedding using morphological knowledge. ACM Transactions on Information Systems (TOIS), 34(1), 4. (pp. 1-25)
[luong2013] Luong, T., Socher, R., & Manning, C. (2013). Better word representations with recursive neural networks for morphology. In Proceedings of the Seventeenth Conference on Computational Natural Language Learning (CoNLL) (pp. 104-113).
[qiu2014] Qiu, S., Cui, Q., Bian, J., Gao, B., & Liu, T. Y. (2014). Co-learning of word representations and morpheme representations. In Proceedings of COLING 2014, the 25th International Conference on Computational Linguistics: Technical Papers (COLING) (pp. 141-150).
[creutz2007] Creutz, M., & Lagus, K. (2007). Unsupervised models for morpheme segmentation and morphology learning. ACM Transactions on Speech and Language Processing (TSLP), 4(1), 3. (pp. 13-34)
[virpioja2013] Virpioja, S., Smit, P., Grönroos, S. A., & Kurimo, M. (2013). Morfessor 2.0: Python implementation and extensions for Morfessor Baseline.
[bojanowski2017] Bojanowski, P., Grave, E., Joulin, A., & Mikolov, T. (2017). Enriching word vectors with subword information. Transactions of the Association for Computational Linguistics, 5, (TACL) (pp. 135-146)
附录
Morfessor中使用的模型实质上是一个隐马尔可夫模型(HMM),该模型与其中用到的算法和思想并非深度学习的范畴,而是统计学习的范畴。为了保证文章的完整性和自涵盖性,同时减少正文的长度,这部分知识放在本部分“附录”中做一介绍。尽管当下(2018年末2019年初)深度学习已经大行其道,然而笔者还是认为统计学习的方法仍然有存在的意义和借鉴的价值
MAP估计
自从概率被数学家用来研究博弈游戏以来,对“概率值的意义是什么”这个问题,一直有两种不同的看法
- 频率学派(frequentist)认为,概率度量的是某个事情发生的频率,是一个“客观”值,这个频率由一个背后客观存在的参数\(\boldsymbol{\theta}\)决定。因此,频率学派解决问题的一个常见思路,就是要求出\(\boldsymbol{\theta}\)最可能的取值,也就是要求出\(\boldsymbol{\theta}\)的最大似然:设数据集为\(\mathbb{X}\),由某个未知的真实数据分布\(p_{\rm data}({\bf x})\)产生;\(p_{\rm model}({\bf x};\boldsymbol{\theta})\)这一概率分布的参数为\(\boldsymbol{\theta}\),\(p_{\rm model}(\boldsymbol{x};\boldsymbol{\theta})\)将输入\(\boldsymbol{x}\)映射到实数来估计真实概率\(p_{\rm data}(\boldsymbol{x})\),则\(\boldsymbol{\theta}_{\rm ML} = \mathop{ {\rm arg}\max}_{\boldsymbol{\theta}} p_{\rm model}(\mathbb{X}; \boldsymbol{\theta})\)。这种方法是最大似然估计法(MLE) 对于有监督学习,似然可以理解为,在给定参数\(\boldsymbol{\theta}\)和数据\(\boldsymbol{x}\)下,得到结果\(\boldsymbol{y}\)的概率。假设\(\boldsymbol{X}\)表示所有输入,\(\boldsymbol{Y}\)是观察到的目标,则最大似然估计有\(\boldsymbol{\theta}_{\rm ML} = \mathop{ {\rm arg}\max}_{\boldsymbol{\theta}}p(\boldsymbol{Y}|\boldsymbol{X};\boldsymbol{\theta})\)
- 贝叶斯学派(Bayesian)认为,概率度量的是观察者对事情发生的把握程度,是一种信念值的体现,是“主观倾向”。尽管贝叶斯学派在建模时也会引入一个参数\(\boldsymbol{\theta}\),但是此时这个参数已经不是一个确定的客观值,而是未知或者不确定的,因此可以表示成一个随机变量。在这种解释下,解决问题的目的是要根据观察到的数据,推测出\(\boldsymbol{\theta}\)的分布,即求出后验概率\(p(\boldsymbol{\theta}|\boldsymbol{x})\)。最好的估计\(\hat{\boldsymbol{\theta}}\)使得其对应的后验概率最大,因此贝叶斯学派常用的解决问题方法称为最大后验概率(MAP)法,得到的估计值是最大后验概率估计(MAP估计, MAPE) 由于根据贝叶斯定律有\(p(\boldsymbol{\theta}|\boldsymbol{x}) \propto p(\boldsymbol{x}|\boldsymbol{\theta})p(\boldsymbol{\theta})\),以及对数函数不改变最大值,因此有\(\boldsymbol{\theta}_{\rm MAP} = \mathop{ {\rm arg}\max}_{\boldsymbol{\theta}} \log p(\boldsymbol{x}|\boldsymbol{\theta}) + \log p(\boldsymbol{\theta})\)。其中\(p(\boldsymbol{x}|\boldsymbol{\theta})\)称为“似然”(可以参考前述“最大似然”的部分),\(p(\boldsymbol{\theta})\)称为“先验概率”,可以理解为在观察到数据前对\(\boldsymbol{\theta}\)的已知知识或者预先判断。这里可以注意到的是,如果假设先验概率是均匀分布,那么MAPE的结果与MLE的结果等价;如果假设先验概率是高斯分布,得到的结果等价于采用了L2正则化的MLE
最好诠释这种差别的例子就是想象如果你的后验分布是双峰的,频率学派的方法会去选这两个峰当中较高的那一个对应的值作为他们的最好猜测,而贝叶斯学派则会同时报告这两个值,并给出对应的概率。
HMM模型
马尔可夫模型
在概率论中,马尔可夫模型是用来对随机变化的系统建模的随机模型,其假设在给定某个当前时刻的状态时,系统未来的状态不依赖于当前时刻之前的状态。即假设该随机过程满足马尔可夫性质。用数学语言描述,如果\(X(t), t > 0\)是一个随机过程,且 \[ p[X(t+h) = y | X(s) = x(s), s \le t] = p[X(t+h)=y|X(t) = x(t)], \forall h > 0 \]
马尔可夫链
假设一个系统有\(N\)个有限的状态\(Q = \{q_1, q_2, \cdots, q_N\}\),系统在时刻\(t\)所处的状态是一个随机变量\(s_t, s_t \in Q\),一般情况下\(s_t\)的具体取值由系统在前\(t-1\)个时刻下的状态共同决定,即 \[ p(s_t=q_i) = p(s_t=q_i|s_{t-1},\cdots, s_1) \] 假设\(s_t\)的具体取值仅由第\(t-1\)个时刻系统的状态\(s_{t-1}\)决定,那么有 \[ \begin{align*} p(s_t = q_i) &= p(s_t = q_i|s_{t-1},\cdots, s_1) = p(s_t = q_i|s_{t-1}) \\ p(s_1, \cdots, s_T) &= p(s_1)\prod_{t=2}^Tp(s_t|s_{t-1}) \end{align*} \] 这时该系统称为离散时间的一阶马尔可夫链。该系统是一种最简单的马尔可夫模型。对于离散时间的k阶马尔可夫链,\(s_t\)的具体取值是由第\(t-1, t-2, \ldots, t-k\)个时刻的状态决定
马尔可夫链可以记为一个三元组\((Q, A, \pi)\),除了状态集合\(Q\)以外,还有
- 一个转移矩阵\(A\)来描述从任意状态\(q_i\)转移到状态\(q_j\)的概率,该矩阵满足两个条件:
- 任意元素均不小于零
- 每行元素的和均为1
- 一个初始概率分布\(\pi\)来描述系统初始状态为\(q_i\)的概率
以下图所示的马尔可夫链为例
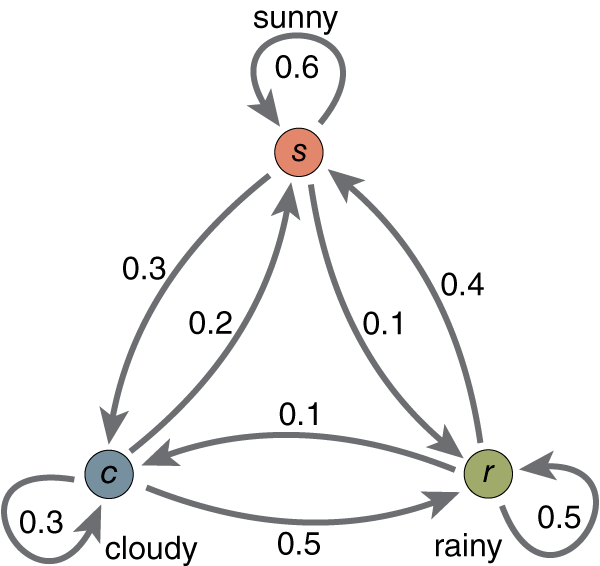
假设三个状态\(q_0 = {\rm sunny}, q_1 = {\rm cloudy}, q_2 = {\rm rainy}\),则对应的转移矩阵\(A\)为 \[ A = \left[\begin{matrix} 0.6 & 0.3 & 0.1 \\ 0.3 & 0.2 & 0.5 \\ 0.4 & 0.1 & 0.5 \end{matrix}\right] \] 进一步假设初始概率分布\(\pi = \left[\begin{matrix}0.4 & 0.2 & 0.4\end{matrix}\right]\)
则系统接连出现出现“云、雨、晴”的概率分别为 \[ \begin{align*} &p(s_0 = q_1, s_1=q_2, s_2=q_0) \\ =& p(s_0=q_1)p(s_1=q_2|s_0=q_1)p(s_2=q_0|s_1=q_2) \\ =& \pi_1 \times A_{12} \times A_{20} \\ =& 0.4 \times 0.5 \times 0.4 = 0.08 \end{align*} \]
隐马尔可夫模型
在隐马尔可夫模型(Hidden Markov Model, HMM)中,系统在任意时刻所处的状态\(q_i\)不再能被外界直接观察到,而是会以一个概率分布向外界展示一个可观察的状态\(o_i\)。这样,系统的实际状态就是“隐藏的”。在自然语言处理中,HMM可以用来对词性标注(POS tag)问题建模,此时系统的隐藏状态是各个单词的词性标注(例如动词、名词、形容词……),可观察状态是单词本身
HMM可以记为一个五元组\((Q,O,A,B,\pi)\),其中
\(Q = \{q_1, q_2, \cdots, q_T\}\)是长度为\(T\)的隐藏序列,每个\(q_i\)都来自于状态表\(S = \{s_1, s_2, \cdots, s_N\}\)
\(O = \{o_1, o_2, \cdots, o_T\}\)是长度为\(T\)的观察序列,每个\(o_i\)都来自于单词表\(V =\{ v_1, v_2, \cdots, v_V\}\)
\(A\)是状态转移矩阵,元素\(a_{ij}\)表示隐藏状态从\(s_i\)迁移到\(s_j\)的概率
\(B\)是发射矩阵,定义当系统处于隐藏状态\(s_i\)时,表现为观察值\(v_j\)的概率,即 \[ \begin{align*} B &= \left[\begin{matrix}b_1(v_1) & b_1(v_2) & \cdots & b_1(v_V) \\ b_2(v_1) & b_2(v_2) & \cdots & b_2(v_V) \\ \vdots & \vdots & \ddots & \vdots \\ b_N(v_1) & b_N(v_2) & \cdots & b_N(v_V)\end{matrix}\right] \\ b_i(v_k) &= p(o_t= v_k|q_t = s_i) \end{align*} \]
\(\pi\)为初始概率分布
也可以简化为一个三元组表示\((A, B, \pi)\)
HMM也做出了两个假设。除了前面介绍的一阶马尔可夫假设(当前隐藏状态只由前一时刻的隐藏状态决定)以外,还有一个输出独立性假设,即当前观察状态只由当前时刻的隐藏状态决定,数学表述为 \[ p(o_i|q_1,\ldots, q_i,\ldots ,q_T, o_1,\ldots, o_i,\ldots,o_T ) = p(o_i|q_i) \] 下图给出了一个HMM的例子:假设你的一个朋友生活在某个不同的城市,你每天可以跟ta聊天知道ta当天做了什么,而且你知道ta每天的行为由天气决定,但是你不能直接得知那个城市的天气。该城市天气的转移图和天气——行为的发射关系由下图决定

记\(s_0 = {\rm rainy}, s_1 = {\rm sunny}, v_0 = {\rm walk}, v_1 = {\rm shop}, v_2 = {\rm clean}\),则系统的转移矩阵\(A\)、发射矩阵\(B\)和初始概率分布\(\pi\)对应为 \[ \begin{align*} A &= \left[\begin{matrix}0.7 & 0.3 \\ 0.4 & 0.6\end{matrix}\right] \\ B &= \left[\begin{matrix}0.1 & 0.4 & 0.5 \\ 0.6 & 0.3 & 0.1\end{matrix}\right] \\ \pi &= \left[\begin{matrix}0.6 & 0.4\end{matrix}\right] \end{align*} \] 对于一个HMM,有三个常见问题
- 似然问题:给定HMM \(\lambda = (A, B, \pi)\)和观察序列\(O\),确定似然\(P(O|\lambda)\)
- 解码问题:给定观察序列\(O\)和HMM \(\lambda = (A, B, \pi)\),确定最有可能的隐藏序列\(Q\)
- 学习问题:给定观察序列\(O\)和HMM的状态集合,学习\(A\)和\(B\)
以下将分别介绍三个问题对应的算法
求解似然问题:前向算法
似然问题是要计算一个给定观察序列\(O\)的概率。以上图给出的模型为例,可以计算模型产生观察状态\(\rm \{walk, shop, walk\}\)的概率。这里的一个难点是,每个观察状态都可能由若干个(可能会是所有\(N\)个)隐藏状态生成。由于前面提到的输出独立性假设,\(p(O|Q) = \prod_{i=1}^Tp(o_i|q_i)\),理论上可以通过穷举所有可能的隐藏状态序列来计算\(O\)的概率,但是由于每个时刻\(o_i\)背后都有\(N\)个可能状态,所以这个计算量是\(O(N^T)\)指数时间的,实际不可行
可以使用动态规划思想来存储中间状态,将算法时间复杂度降低到\(O(N^2T)\)。记\(\alpha_t(j) = p(o_1, o_2, \ldots, o_t, q_j = s_j|\lambda)\),则有如下的递推关系(假设\(o_t = v_k\)) \[ \alpha_t(j) = \sum_{i=1}^N\alpha_{t-1}(i)a_{ij}b_j(v_k) \] 即对\(t\)时刻的隐藏状态\(s_j\),要计算出其展示出\(o_1,o_2,\ldots, o_{t}\)的概率,有三步
- 求出\(t-1\)时刻任意隐藏状态\(s_i\)展示出\(o_1, o_2, \ldots, o_{t-1}\)的概率\(\alpha_{t-1}(i)\)(上一步的结果)
- 求出\(t-1\)时刻隐藏状态\(s_{i}\)转移到\(t\)时刻\(s_t\)的状态\(a_{ij}\)(直接查表可得)
- 求出\(t\)时刻隐藏状态\(s_j\)展示出\(v_k\)的概率\(b_j(v_k)\)(直接查表可得)
三者相乘即可。由于\(t-1\)时刻可能的隐藏状态有\(N\)个,因此需要将这\(N\)个概率相加
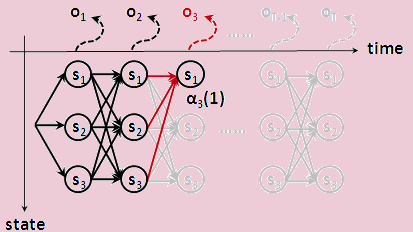
上图给出了前向算法的示意图,具体实现代码如下
1 | def forward(obs, hmm): |
求解解码问题:维特比算法
解码问题是要对给定的观察序列,找出最可能产生这个观察序列的隐藏序列。尽管理论上也可以穷举所有隐藏序列,计算该序列产生给定观察序列的概率,进而找到最优隐藏序列,但是由前文易知这种方法不可行。应对方法也是使用动态规划算法,并引入一个中间变量\(\psi_t(j)\),表示在经历了隐藏状态\(q_1, \ldots, q_{t-1}\)以后,系统在第\(t\)时刻位于隐藏状态\(s_j\)的概率,即 \[ \psi_t(j) = \max_{q_1, \cdots, q_{t-1}}p(q_1, \cdots, q_{t-1}, o_1, \cdots, o_t, q_t=s_j|\lambda) \] 这里也存在一个递推关系(同样假设\(o_t = v_k\)): \[ \psi_t(j) = \max_{i=1}^N \psi_{t-1}(i)a_{ij}b_{j}(v_k) \] 可以看出维特比算法与前向算法类似,区别主要在于两点。其一是维特比算法每一步都是求最大值,而前向算法是求累加值;其二是由于维特比算法需要给出最可能的隐藏状态序列,因此需要维护一个指针(或一个列表),来得出最后的序列结果
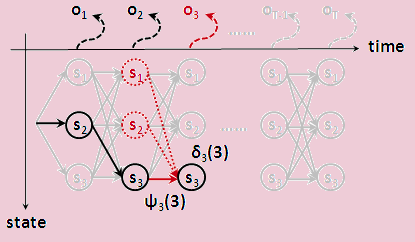
上图给出了维特比算法的示意图,具体实现代码如下
1 | def viterbi(observations, hmm): |
求解学习问题:前向-后向算法(Baum-Welch算法)
学习问题是如何根据一个给定的观察序列学习HMM的状态转移矩阵\(A\)和发射矩阵\(B\)。使用的算法Baum-Welch算法是“期望最大算法”(Expectation-Maximization, EM算法)的一种特例情况。在介绍算法之前,需要先引入一个与前面介绍的“前向概率”\(\alpha_t(j)\)相对应的概率——“后向概率”\(\beta_t(i)\)。前向概率指的模型展现出\(o_1, \cdots, o_{t-1}\)这\(t-1\)个观察状态,并在第\(t\)时刻落在隐藏状态\(s_j\)的概率,而后向概率指的是模型在第\(t\)时刻落在隐藏状态\(s_i\)的条件下,展现出\(o_{t+1}, \cdots, o_T\)这\(T-t\)个观察状态的概率,即\(\beta_t(i) = p(o_{t+1}, o_{t+2}, \ldots, o_T|q_t = i, \lambda)\)。递推关系为
\[ \beta_t(i) = \sum_{j=1}^N a_{ij}b_j(o_{t+1})\beta_{t+1}(j) \] 接下来利用\(\alpha_t(i)\)和\(\beta_{t+1}t(j)\)估计状态转移矩阵中的每个元素\(a_{ij}\)。最直观的做法是使用最大似然法,有 \[ \hat{a}_{ij} = \frac{从状态i到状态j这一转换的期望数量}{从状态i发出的转换的期望数量} \] 如何计算分子呢?假设能估计出时刻\(t\)发生转换\(i\rightarrow j\)的概率,那么将它们累加起来就可以估计出转换\(i\rightarrow j\)的总数。形式化地,可以定义给定模型\(\lambda\)和观察序列\(O\)时,模型在\(t\)时刻位于隐藏状态\(s_i\)且在\(t+1\)时刻位于隐藏状态\(s_j\)的概率\(\xi_t(i, j)\): \[ \xi_t(i, j) = p(q_t=s_i, q_{t+1}=s_j|O, \lambda) \] 修改一下条件概率,可以得到一个类似的概率值\(\zeta_t(i,j)\) \[ \zeta_t(i, j) = p(q_t = s_i, q_{t+1}=j, O|\lambda) \] \(\zeta_t(i,j)\)的值相对容易计算: \[ \zeta_t(i,j) = \alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j) \] 又由于 \[ p(X|Y,Z) = \frac{p(X, Y|Z)}{p(Y|Z)} \] 所以只需求出\(p(O|\lambda)\)为 \[ p(O|\lambda) = \sum_{j=1}^N\alpha_t(j)\beta_t(j) \] 因此 \[ \xi_t(i,j) = \frac{\zeta_t(i,j)}{p(O|\lambda)} = \frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum_{j=1}^N \alpha_t(j)\beta_t(j)} \] 累加可得(注意模型有\(N\)个隐藏状态) \[ \hat{a}_{ij} = \frac{\sum_{t=1}^{T-1}\xi_t(i,j)}{\sum_{t=1}^{T-1}\sum_{k=1}^N \xi_t(i, k)} \] 类似地可以求出发射矩阵中的每个元素:由最大似然法有 \[ \hat{b}_j(v_k) = \frac{系统在隐藏状态j展现出观察状态k的期望次数}{系统处于隐藏状态j的期望次数} \] 先定义给定模型为\(\lambda\)和观察序列\(O\)时,系统处于隐藏状态\(s_j\)的概率\(\gamma_t(j) = p(q_t =s_j|O,\lambda)\)。相同地,有 \[ \gamma_t(j) = \frac{p(q_t=j,O|\lambda)}{p(O|\lambda)} \] 其中\(p(q_t = j, O|\lambda) = \alpha_t(j)\beta_t(j)\)。最后有 \[ \hat{b}_j(v_k) = \frac{\sum_{t=1\ {\rm s.t.\ }o_t=v_k}^T \gamma_t(j)}{\sum_{t=1}^T \gamma_t(j)} \] 整个Baum-Welch算法/前向-后向算法的过程因此可以简单描述为:
- 初始化\(A\)和\(B\)
- 迭代如下过程直至收敛
- E步:计算\(\gamma_t(j)\)和\(\xi_t(i,j)\)
- M步:计算\(\hat{a}_{ij}\)和\(\hat{b}_j(v_k)\)
参考文献
花书第五章
维基百科相关词条
《语音与语言处理(第三版·草稿)》,Dan Jurafsky and James H. Martin. 附录A:隐马尔可夫模型
《统计自然语言处理(第二版)》,宗成庆. 第六章
