NMT Tutorial 3. 神经网络语言模型与词向量

本文主要参考了如下教程

Koehn2017 : 第2、3节，第4节前半部分
Neubig2017 : 第5章
StanfordCS224n : 第2、3、4讲
Goldberg NNMNLP : 第3、4、5、8、9、10、11章

其中主要会以[Neubig2017]和[StanfordCS224n]的内容为主

神经网络

关于神经网络的一些基本细节，例如基本概念、反向传播的思想等等，在博客的其它文章里（如林轩田老师的机器学习技法、Hinton的Coursera课程）有过介绍，这里就不赘述了。这里想就着斯坦福大学CS224n第四讲的内容从矩阵的层面上给出反向传播梯度的计算方法

一个示例结构

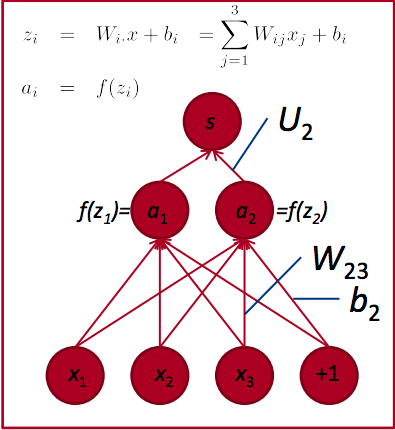
上图给出了一个示例神经网络，各层参数与输入、输出及其它记号如下

输入向量\(\boldsymbol{x} \in \mathbb{R}^{3 \times 1}\)
输入层到隐藏层的权重\(\boldsymbol{W} \in \mathbb{R}^{2 \times 3}\)，同时还包括一个偏置向量\(\boldsymbol{b} \in \mathbb{R}^{2 \times 1}\)
隐藏层向量在激活前是\(\boldsymbol{z}\in \mathbb{R}^{2 \times 1}\)，激活函数是\(f\)，向量激活后为\(\boldsymbol{a} \in \mathbb{R}^{2 \times 1}\)
隐藏层到输出层的权重\(\boldsymbol{U} \in \mathbb{R}^{2 \times 1}\) （按照约定的记法，向量用小写粗体，矩阵用大写粗体，这里应该写为\(\boldsymbol{u}\)。不过为了与原课件对应，这里没有这样做）
神经网络的输出结果为一个标量 \(s\)

按照如上约定， \(s\) 的计算过程向量化表示如下 \[ \begin{align*} s &= \boldsymbol{U}^\mathsf{T}\boldsymbol{a} \\ &= \boldsymbol{U}^\mathsf{T}f(\boldsymbol{z}) \\ &= \boldsymbol{U}^\mathsf{T}f(\boldsymbol{Wx}+\boldsymbol{b}) \end{align*} \] 或者分变量写出，成为如下形式 \[ \begin{align*} s &= \boldsymbol{U}^\mathsf{T}\boldsymbol{a} \\ \boldsymbol{a} &= f(\boldsymbol{z}) \\ \boldsymbol{z} &= \boldsymbol{Wx} + \boldsymbol{b} \end{align*} \]

按照梯度下降的原理，训练模型时需要得到损失函数\(J\)对每个参数的梯度。例如，对于参数\(\boldsymbol{W}\)，需要计算\(\frac{\partial J}{\partial \boldsymbol{W}}\)。根据反向传播算法和导数的链式法则，有 \[ \frac{\partial J}{\partial \boldsymbol{W}} = \frac{\partial J}{\partial s}\cdot \frac{\partial s}{\partial \boldsymbol{W}} \] 其中，第一项\(\frac{\partial J}{\partial s}\)如何计算应该视具体的损失函数计算方法而定，与参数本身无关。因此对任意参数，只需要关注网络输出\(s\)对该参数的偏导即可

从矩阵元素看如何计算梯度

（这一部分讲得比较详细但是也很繁琐，不感兴趣的可以跳过）

要计算\(\frac{\partial s}{\partial \boldsymbol{W}}\)，可以首先考虑如何计算\(\frac{\partial s}{\partial W_{ij}}\) 。由\(s\) 的计算方法，有 \[ \frac{\partial s}{\partial W_{ij}} = \frac{\partial}{\partial W_{ij}}\boldsymbol{U}^\mathsf{T}\boldsymbol{a} \] 由前图，每个\(\boldsymbol{W}_{i\cdot}\)只与\(a_i\) 相关，\(a_i\)又只与\(U_ia_i\)相关，因此 \[ \frac{\partial}{\partial W_{ij}}\boldsymbol{U}^\mathsf{T}\boldsymbol{a} = \frac{\partial }{\partial W_{ij}}U_ia_i \]

由于\(U_i\)与\(W_{ij}\)无关，因此可以提出来。代入其它变量定义，并将\(f\)的导数记作\(f'\)（因为可选的激活函数有很多种），可以得到 \[ \begin{align*} \frac{\partial}{\partial W_{ij}}U_ia_i &= U_i \frac{\partial}{\partial W_{ij}}a_i \\ &= U_i \frac{\partial a_i}{\partial z_i} \frac{\partial z_i}{\partial W_{ij}} \\ &= U_i \frac{\partial f(z_i)}{\partial z_i}\frac{\partial z_i}{\partial W_{ij}} \\ &= U_i f'(z_i)\frac{\partial z_i}{\partial W_{ij}} \\ &= U_i f'(z_i)\frac{\partial (\boldsymbol{W}_{i\cdot}\boldsymbol{x} + b_i)}{\partial W_{ij}} \\ &= U_i f'(z_i) \frac{\partial }{\partial W_{ij}}\sum_kW_{ik}x_k \\ &= U_i f'(z_i) x_j \end{align*} \] 如果将\(U_if'(z_i)\)看做一个整体，记作\(\delta_i\)，那么有 \[ \frac{\partial s}{\partial W_{ij}} = \delta_ix_j \] 由于标量\(y\)对矩阵\(\boldsymbol{X} \in \mathbb{R}^{m \times n}\)的求导法则为 \[ \frac{\partial y}{\partial \boldsymbol{X}} = \left[\begin{matrix}\frac{\partial y}{\partial X_{11}} & \cdots & \frac{\partial y}{\partial X_{1n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y}{\partial X_{m1}} & \cdots &\frac{\partial y}{\partial X_{mn}}\end{matrix}\right] \] 因此 \[ \begin{align*} \frac{\partial s}{\partial \boldsymbol{W}} &= \left[\begin{matrix}\frac{\partial s}{\partial W_{11}} & \frac{\partial s}{\partial W_{12}} & \frac{\partial s}{\partial W_{13}} \\ \frac{\partial s}{\partial W_{21}} & \frac{\partial s}{\partial W_{22}} & \frac{\partial s}{\partial W_{23}}\end{matrix}\right] \\ &= \left[\begin{matrix} \delta_1x_1 & \delta_1x_2 & \delta_1x_3 \\ \delta_2x_1 & \delta_2x_2 & \delta_2x_3\end{matrix}\right] \\ &= \boldsymbol{\delta}\boldsymbol{x}^\mathsf{T} \end{align*} \] 其中\(\boldsymbol{\delta} \in \mathbb{R}^{2\times 1}\)可以看作是来自激活\(\boldsymbol{a}\)的误差信号

将上面的推导过程换做对\(b_i\)求导，不难得出 \[ \frac{\partial s}{\partial \boldsymbol{b}} = \boldsymbol{\delta} \] 在NLP应用中，\(\boldsymbol{x}\)通常是一个词向量，因此也需要被训练（具体介绍在本文后面的小节中）。在计算\(\frac{\partial s}{\partial x_1}\)的过程中，要注意的是\(x_1\)与两个激活值都相连，因此要做一个求和。为了更直白地说明为什么需要做求和，可以想象一个最简单的神经网络，该网络的输入层只有一个节点\(x_1\)，也没有偏置项；隐藏层和输出层与上图一样。那么，为了求\(s\)，就有\(s = U_1f(z_1) + U_2f(z_2) = U_1f(W_{11}x_1) + U_2f(W_{21}x_1)\)，两个求和项里都出现了变量\(x_1\)，因此求偏导时需要有一个加和的过程

具体计算与上面求\(\frac{\partial s}{\partial W_{ij}}\) 类似，这里略过。最后可以得到 \[ \begin{align*} \frac{\partial s}{\partial x_j} &= \sum_{i=1}^2U_if'(z_i)W_{ij} = \sum_{i=1}^2\delta_iW_{ij} \\ &= \boldsymbol{W}_{\cdot j}^\mathsf{T}\boldsymbol{\delta} \end{align*} \] 那么按照前面标量对向量/矩阵的求导法则有 \[ \frac{\partial s}{\partial \boldsymbol{x}} = \boldsymbol{W}^\mathsf{T}\boldsymbol{\delta} \]

从矩阵微分看如何计算梯度

如果对矩阵/向量的微分法则记得比较清楚，就可以不用上述比较繁琐的推导过程。具体规则表可以见Wiki词条：Matrix calculus，或者参考Towser大神的《机器学习中的矩阵/向量求导》。求导过程中，时刻检查各变量的维度，并记住标量对矩阵/向量求导，最后得到同维度的矩阵/向量就可以。由 \[ \begin{align*} s &= \boldsymbol{U}^\mathsf{T}\boldsymbol{a} \\ \boldsymbol{a} &= f(\boldsymbol{z}) \\ \boldsymbol{z} &= \boldsymbol{Wx} + \boldsymbol{b} \end{align*} \] 可知 \[ \begin{align*} \frac{\partial s}{\partial \boldsymbol{a}} &= \boldsymbol{U} = \boldsymbol{\delta}_1\\ \frac{\partial s}{\partial \boldsymbol{z}} &= \frac{\partial s}{\partial \boldsymbol{a}}\cdot \frac{\partial \boldsymbol{a}}{\partial \boldsymbol{z}} = \boldsymbol{\delta_1} \odot f'(\boldsymbol{z}) = \boldsymbol{\delta} \\ \frac{\partial s}{\partial \boldsymbol{W}} &= \frac{\partial s}{\partial \boldsymbol{z}}\cdot \frac{\partial \boldsymbol{z}}{\partial \boldsymbol{W}} = \boldsymbol{\delta}\boldsymbol{x}^{\mathsf{T}} \\ \frac{\partial s}{\partial \boldsymbol{b}} &= \frac{\partial s}{\partial \boldsymbol{z}}\cdot \frac{\partial \boldsymbol{z}}{\partial \boldsymbol{b}} = \boldsymbol{\delta} \\ \frac{\partial s}{\partial \boldsymbol{x}} &= \frac{\partial s}{\partial \boldsymbol{z}}\cdot \frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}} = \boldsymbol{W}^\mathsf{T}\boldsymbol{\delta} \end{align*} \]

激活函数

本小节对激活函数的比较部分来自于CS231n讲义

神经网络的精髓在于激活函数的使用。激活函数通常是非线性的，否则堆叠多个线性隐藏层的网络效果等同于一个线性模型。假设对于某个隐藏层节点，该节点与前面一层所有节点都连接（称为全连接，例如前面示例图中的\(a_1\)节点。如果这一层中所有节点都是全连接的，那么这一层可以称为全连接层），那么该节点的输入权重可以看作是对前一层所有节点的组合。而非线性激活函数的效果可以非形式化地理解为，给定前一层节点的输入和权重，该节点被“打开”的程度。因此，使用非线性激活函数以后，神经网络每一个隐藏层的节点都可以看做是一个组合特征的提取器：对某些输入，节点打开，该组合特征有效；对某些输入，节点关闭，该组合特征无效；对某些输入，节点半开，该组合特征起一定作用

常见的激活函数包括以下几种：

sigmoid激活函数，形式为\(\sigma(x) = (1+e^{-x})^{-1}\)，值域为\((0, 1)\)。这个激活函数非常经典，但是存在一些比较严重的问题：
- 容易饱和（saturate），进而杀死梯度。当sigmoid函数值接近0或1时，由于其导数为\(\sigma'(x) = \sigma(x)(1-\sigma(x))\)，所以梯度接近0。而反向传播实际上会对多个梯度做连乘（参见上面的推导过程），因此当激活函数的梯度为0时，很容易将梯度“杀死”，使得底层神经元接收不到更新信号。此外，如果初始化不当使得权重的初始值比较大，那么使用sigmoid函数会非常容易出现饱和的现象，神经网络几轮之后就学不到东西了
- 输出不以零为中心。使用sigmoid激活函数会让网络靠近输出层部分的神经元接收到的数据不以0为中心。如果神经元的输入总是大于0的，那么权重的梯度在反向传播中要么全都是正的，要么全都是负的，因此会造成学习过程中权重更新量的抖动。当然，如果用的是小批量梯度下降更新权重，那么一个批次内这样的更新量会正负抵消一些，因此会有些为正有些为负，所以这个问题相比而言不是那么严重了
双曲正切函数，形式为\(\tanh(x) = (e^x-e^{-x})/(e^x+e^{-x})\)，值域为\((-1, 1)\)。这种激活函数也存在饱和问题，但是输出会以0为中心。因此在应用时，总是应该优先考虑tanh而不是sigmoid。此外，tanh也可以看作是经过缩放的sigmoid函数，因为\(\tanh(x) = 2\sigma(2x) - 1\)
整流线性单元，形式为\({\rm ReLU}(x) = \max(0, x)\)。这种激活函数在近几年受到了广泛的重视和应用，效果很好
- 相比于sigmoid/tanh，ReLU可以加速SGD的收敛。怀疑是因为其线性、非饱和的性质
- ReLU的计算特别简单
- 但是，当\(x<0\)时，ReLU的前向传播结果和梯度都为0，因此这个神经元就永远不会被激活了。如果适当地设置学习率，这种情况发生的频率可能会低一些
Leaky ReLU，形式为 \[ {\rm LeakyReLU}(x) = \begin{cases}\alpha x & {\rm if\ }x < 0 \\ x & {\rm elsewhere}\end{cases} \] 其中\(\alpha\)通常是一个特别小的值，例如0.01。Leaky ReLU提出的初衷是为了解决ReLU单元容易死掉的问题，一些人的工作中也表明能观察到这样的效果，但是并没有系统研究表明这种做法总是奏效的。何恺明等人提出的PReLU是让每个神经元都有不同的\(\alpha\)，不过也没有证据说明其它任务能有同样好的效果
maxout，形式为\(\max(\boldsymbol{W}_1^\mathsf{T}\boldsymbol{x}, \boldsymbol{W}_2^\mathsf{T}\boldsymbol{x}, \ldots)\)。原有的两层之间只有一组参数，maxout则是训练\(k\)组参数，这样可以得到\(k\)组向量。然后，在每个维度上，选择最大的那一个。这种做法取了ReLU的精华（方便计算，没有饱和问题），弃了ReLU的糟粕（不会有神经元死亡），不过要学习的参数成倍增加

原始讲义推荐使用ReLU，不过要小心设置学习率。如果神经元死亡是个问题，转用Leaky ReLU或者maxout。永远不要尝试sigmoid，可以试试tanh，但是tanh一般要比ReLU及其变种差。不过花书指出RNN、许多概率模型和一些自编码器会有一些额外要求因此不能使用分段线性激活函数（例如ReLU），因此可以尝试sigmoid

更多的激活函数比较可以参见相关维基词条

自动微分

由于反向传播的过程中涉及大量梯度的计算，计算起来会比较复杂，容易出错。而且有一些值会重复计算，如果每次都重新算一遍，效率也是问题。一般来讲，编程框架会把计算过程组织成一个计算图，然后使用自动微分的方法完成两个步骤：第一个步骤是通过拓扑顺序遍历节点做一个前向计算，得出实际结果；第二个步骤是以“反拓扑”的顺序做一个后向计算，得到梯度

关于自动微分的具体细节将在之后的补充文章中介绍

神经网络语言模型

假设词汇表大小为\(|V|\)，要训练一个三元Loglinear语言模型，那么通常会训练两个\(|V| \times |V|\)的权重矩阵\(\boldsymbol{W}^{(1)}\)和\(\boldsymbol{W}^{(2)}\)（也可以看作是一个\(|V| \times 2|V|\)的权重矩阵），然后根据上文两个单词的ID从矩阵中选出对应的列，将两者与训练出来的截距\(\boldsymbol{b}\)求和，最后计算一个softmax得到下一个词的概率分布，即 \[ \begin{align*} \boldsymbol{s} &= \boldsymbol{W}^{(1)}_{\cdot,{\rm ID}_1} + \boldsymbol{W}^{(2)}_{\cdot ,{\rm ID}_2} + \boldsymbol{b} \\ \boldsymbol{p} &= {\rm softmax}(\boldsymbol{s}) \end{align*} \]

神经网络语言模型也要训练权重和偏置，不过通常来讲，需要至少一个隐藏层和一个非线性变换（激活函数），也就是要训练两套权重，以及一个词嵌入矩阵。最简单的含有一个隐藏层的网络结构如下： \[ \begin{align*} \boldsymbol{m} &= {\rm concat}(\boldsymbol{M}_{\cdot, {\rm ID}_1}, \boldsymbol{M}_{\cdot, {\rm ID}_2}) \\ \boldsymbol{h} &= \tanh (\boldsymbol{W}_{mh}\boldsymbol{m} + \boldsymbol{b}_h) \\ \boldsymbol{s} &= \boldsymbol{W}_{hs}\boldsymbol{h} + \boldsymbol{b}_s \\ \boldsymbol{p} &= {\rm softmax}(\boldsymbol{s}) \end{align*} \] 其中\(\boldsymbol{M}\)是词嵌入矩阵，形状为\(L_m \times |V|\)，\(L_m\) 是一个超参数。\(\rm concat\)是向量的拼接操作，适用于位置信息重要的情况（如果位置信息不重要，也可以考虑引入加权求和）。尽管直觉上\(L_m\)应该越大越好，但是[Britz2017]通过实验指出在机器翻译领域128维的词向量已经足以给出不错的效果。这样，矩阵的每一列都是词表\(V\)中一个单词的向量表示，或者说是嵌入，其中词向量的每个维度可以看作是数值表示了单词某个特征（不过并不好说具体是什么特征，可以说，每个特征都是魔幻的）

回忆前面介绍的独热编码方式，可以看出那是一种稀疏表示：每个词的编码长度都是 \(|V|\)，但是只有一个维度是1其余维度都是0。在这种方式下，所有单词都是独立的——对于两个向量\(\boldsymbol{u}, \boldsymbol{v}\)，通常使用余弦距离来衡量两个向量的相似度： \[ {\rm sim}(\boldsymbol{u}, \boldsymbol{v}) = \cos \theta = \frac{\boldsymbol{u} \cdot \boldsymbol{v}}{\|\boldsymbol{u}\|\cdot\|\boldsymbol{v}\|} \] 显然，如果使用独热编码表示单词，那么任意两个单词的内积都是0，所以此时词向量构成的空间里所有词向量都是两两正交的。但是使用神经网络语言模型训练出的词向量是一种稠密表示，向量的每个维度都是一个实数，并代表了一定的意义（尽管是什么意义很难解释）。而且，词向量训练的结果会使得意思相近的词对应的向量的距离也比较小，因此使得模型对上下文的泛化能力更强。例如，假设模型在预测阶段见到的上文是horses consume，这个词组在训练阶段没有见过，但是训练集里有大量类似于cow eats grass这样的词组，那么传统的N元语法就会束手无策。然而对于神经网络语言模型来说，一方面cow-cows, cows-horses, eats-eat, eat-consume这些单词对的词向量存在着某种相似性，另一方面隐藏单元实际上起到了特征提取器的效果，隐含做了特征组合（线性模型无法学到这些知识，除非手动表示特征之间的交互并建立成新特征送给模型），因此模型就会推断出来后面应该是grass。此外，模型甚至可以学到非相邻词之间的关系（例如中心词可能是受到倒数第二个和倒数第五个单词的影响，与倒数第一、三、四个单词无关）。因此，神经网络语言模型兼具了更好的鲁棒性和灵活性

不过，泛化是一把双刃剑，在某些情况下，过度的泛化能力会造成意想不到的不好的后果。例如，假设训练集里有很多brown horse, white horse, black horse的搭配，而评测时要给blue horse一个概率。传统的N元语法倾向打个低分，但是神经网络语言模型可能会因为blue与其他颜色词的相似性给出一个不太低的分数，从而偏离人们的预期。因此，机器翻译中如果同时使用统计语言模型（例如Kneser-Ney平滑的模型）和神经模型，可以提高翻译质量：神经模型提供泛化能力，处理训练时没见到的情况，而传统模型对过于泛化的情况进行惩罚

尽管在多数情况下，使用稠密表示的单词向量比稀疏表示的独热编码效果要好，但是两者之间也有一个潜在的联系：大部分情况下，神经网络接受的输入还是一个独热编码，但是会使用该独热编码从嵌入矩阵中获得对应的词向量（这个过程也称为“查找过程”，是TensorFlow里tf.nn.embedding_lookup这个函数所完成的功能）。此外，不仅是单词可以做嵌入表示，其它在传统方法里使用独热编码的元素，例如POSTAG等，也都可以使用类似的思想做成稠密向量

经典词向量算法

尽管神经网络语言模型在2003年就被[Bengio2003]首先提出，词的稠密向量表示方法也在2010年被[Turian2010]讨论，但是词向量真正受到广泛关注还是在2013年Mikolov的标志性论文提出以后。本篇文章接下来将介绍Mikolov 2013年提出的经典的词向量算法word2vec，以及CS224n里提到的GloVe。近几年涌现的新的算法将在后续补充文章中介绍

Word2Vec

在最初始的Word2Vec论文[Mikolov2013a]中，神经网络语言模型和词向量两者是分开训练的。其中，词向量的训练并没有用到隐藏层，所以实际上就是根据中心词和上下文单词训练一个loglinear模型。这里背后蕴含的思想是，词的意思可以由语境确定，如果你能预测出这个单词在什么语境下出现，你就理解了这个单词的意思

文章提出了两种不同的模型结构

连续词袋模型（Continuous Bag-of-Words Model, CBOW）的输入是某个单词上下文共\(N\)个词（文章中给出的是前四个词和后四个词）。模型从词嵌入矩阵中找到这8个单词id对应的向量，做一个简单求和，然后用和向量去预测中间词，因此模型的计算复杂度为\(Q = N \times D + D \times \log_2(V)\)，其中\(D\)为词向量长度，\(V\)为词表大小。取对数的原因是因为投影层作者没有使用普通的softmax，而是采用了分层softmax的方法。这个方法在后面介绍。可以注意到，上下文单词的顺序对模型没有影响，因为模型使用了一个求和过程，该过程与顺序无关。这也是模型里”词袋“一词的意义
连续skip-gram模型（Continuous skip-gram Model）的输入是某个单词本身。不同于CBOW使用上下文单词预测中心词的做法，skip-gram的做法是利用中心词预测一定范围内的上下文单词。CBOW利用的是多个单词，skip-gram用的是一个单词。由于距离越远的词与中心词关系也越远，因此通常在采样时减少取到这些单词的概率。该模型的计算复杂度为\(Q = 2R \times (D+D\times \log_2(V))\)。假设\(C\)是上下文单词数量，则\(R = {\rm randrange}(1, C + 1)\)。文中给出的\(C=10\)

上图给出了CBOW和skip-gram的示意图。注意前面计算的\(Q\)都是计算复杂度，而不是参数数量。两个算法的参数数量都是\(2VD\)，其中一半是输入单词的词向量表示，一半是输出单词

在提出CBOW和skip-gram两种词向量训练方法以后，Mikolov等人又在[Mikolov2013b]中对skip-gram做了一些扩展。文章首先更加形式化定义了skip-gram模型训练时用到的目标函数：给定一串训练时用到的单词序列\(w_1, w_2, \ldots, w_T\)，skip-gram模型是要最大化概率对数值的平均值，即 \[ \frac{1}{T}\sum_{t=1}^T\sum_{-c \le j \le c, j\not=0} \log p(w_{t+j}|w_t) \] 其中\(c\)是训练时上下文单词的个数（可以是中心词\(w_t\)的一个函数）。\(c\)越大，模型的准确率越高，但是训练时间越长。原始的skip-gram模型里将\(p(w_{t+j}|w_t)\)定义为一个softmax函数 \[ p(w_O|w_I) = \frac{\exp\left(\boldsymbol{v}_{w_O}'^\mathsf{T}\boldsymbol{v}_{w_I}\right)}{\sum_{w=1}^W\exp\left(\boldsymbol{v}_{w}'^\mathsf{T}\boldsymbol{v}_{w_I}\right)} \] 其中\(\boldsymbol{v}_w\)和\(\boldsymbol{v}_w'\)是\(w\)的”输入向量表示“和”输出向量表示“，\(W\)是词表大小。通常情况下因为\(W\)很大（\(10^5\)到\(10^7\)项）且梯度的计算量正比于\(W\)，因此不会直接这么做，会引入一些优化

分层Softmax

采用分层softmax（hierarchical softmax）可以把算法的复杂度从\(O(W)\)降低到\(O(\log W)\)，方法是在输出层构建一棵二叉树，把每个单词当做是叶子节点，并在构建树时隐含地表示子节点之间的相对概率关系：每个单词\(w\)都存在唯一一条可以到达树根的路径，那么令\(n(w, j)\)是从根到单词\(w\)路径上的第\(j\)个节点，\(L(w)\)是路径的长度（因此\(n(w, 1) = {\rm root}\)，\(n(w, L(w)) = w\)）。对所有内部结点\(n\)，令\({\rm ch}(n)\)为其某个孩子，并令\([\![x]\!]\)在\(x\)为真时为1否则为-1，则使用分层softmax方法，\(p(w_O|w_I)\)定义为 \[ p(w|w_I) = \prod_{j=1}^{L(w)-1}\sigma\left([\![n(w, j+1) = {\rm ch}(n(w, j))]\!] \cdot \boldsymbol{v}_{n(w,j)}'^\mathsf{T}\boldsymbol{v}_{w_I}\right) \] 其中\(\sigma\)是sigmoid函数。使用分层softmax的方法可以使得\(\log p(w_O|w_I)\)和\(\nabla \log p(w_O|w_I)\)的计算代价都正比于\(L(w_O)\)，平均情况下不会大于\(\log W\)。而且对一般的softmax方法，每个单词会对应两个不同的嵌入表示\(\boldsymbol{v}_w\)和\(\boldsymbol{v}_w'\)，而分层softmax只有一个\(\boldsymbol{v}_w\)，另外对二叉树的每个内部结点\(n\)会有一个嵌入表示\(\boldsymbol{v}_n'\)。文章使用的二叉树为Huffman树

负采样

Gutmann和Hyvärinen曾经在[Gutmann2012]中提出过一种“噪声对比估计”（Noise Contrastive Estimation, NCE）的方法，思想是好的模型应该能够通过logistic回归这些手段将数据从噪声中分辨出来。Skip-gram采用了这种方法的简化形式，称为负采样（Negative sampling, NEG），并将其作为分层softmax的一种替代方案。采用负采样的算法将skip-gram目标函数中所有\(\log P(w_O|w_I)\)替换成如下形式 \[ \log \sigma(\boldsymbol{v}_{w_O}'^\mathsf{T}\boldsymbol{v}_{w_I}) + \sum_{i=1}^k \mathbb{E}_{w_i \sim P_n(w)}\left[\log \sigma(-\boldsymbol{v}_{w_i}'^\mathsf{T}\boldsymbol{v}_{w_I})\right] \] 也就是要把目标单词\(w_O\)与使用噪声分布\(P_n(w)\)生成的其它词利用logistic回归方法来分开，其中对每条数据使用\(k\)个负样本。对小数据集，\(k\)一般取5到20，而大数据可以是2到5。NEG与NCE最大的区别是NCE在需要噪声分布的样本的同时还需要概率值，但是NEG只需要负样本。实验中给出最好的\(P_n(w)\)是一元词概率的3/4次方，即\(U(w)^{3/4}/Z\)（文章中没有指明\(Z\)的意义，应该是归一化项）

[Goldberg2014]对负采样的过程做了更详细的解释。首先需要再次明确的是，使用负采样的skip-gram实际上优化的是一个不同的目标函数。记\(w\)为一个中心词，\(c\)是一个目标词，\(D\)是从语料库中抽取的所有单词-上下文对，令\(p(D=1|w, c)\)是\((w, c)\)出现在训练语料中的概率，\(p(D=0|w,c)=1-p(D=1|w,c)\)是\((w, c)\)没有出现在训练语料中的概率，模型参数为\(\boldsymbol{\theta}\)，那么新的目标是找到最好的参数\(\boldsymbol{\theta}\)，满足 \[ \begin{align*} &\mathop{ {\rm arg}\max}_\boldsymbol{\theta} \prod_{(w,c) \in D}p(D=1|w,c;\boldsymbol{\theta}) \\ = &\mathop{ {\rm arg}\max \log}_\boldsymbol{\theta} \prod_{(w,c) \in D}p(D=1|w,c;\boldsymbol{\theta}) \\ = &\mathop{ {\rm arg}\max}_\boldsymbol{\theta} \sum_{(w,c) \in D} \log p(D=1|w,c;\boldsymbol{\theta}) \\ \end{align*} \] 其中 \[ p(D=1|w,c;\boldsymbol{\theta}) = \frac{1}{1+\exp\{-\boldsymbol{v}_c^\mathsf{T}\boldsymbol{v}_w\}} \] 因此新的目标函数就是 \[ \mathop{ {\rm arg}\max}_\boldsymbol{\theta} \sum_{(w,c) \in D}\log \frac{1}{1+\exp\{-\boldsymbol{v}_c^\mathsf{T}\boldsymbol{v}_w\}} \] 对于这个目标函数，如果找到一个参数\(\boldsymbol{\theta}\)，使得对每个单词对\((w, c)\)都有\(p(D=1|w,c;\boldsymbol{\theta})\)，那么效果肯定特别好。具体地，只要这个\(\boldsymbol{\theta}\)使得对所有\(\boldsymbol{v}_c\)和\(\boldsymbol{v}_w\)有\(\boldsymbol{v}_c = \boldsymbol{v}_w\)且\(\boldsymbol{v}_c^\mathsf{T}\boldsymbol{v}_w = K\)（其中\(K\)是一个足够大的数，40就可以），那么就能达到前面说的效果。但是，肯定不希望所有向量都相等，因此需要加入一些方法来做限制，比如禁掉某些单词对，即告诉模型对某些\((w,c)\)，\(p(D=1|w,c;\boldsymbol{\theta})\)一定非常低，这样的单词对一定不会在数据集中出现。因此，可以通过随机生成一些\((w, c)\)对，构成新的数据集\(D'\)，并假设\(D'\)这里的数据都是“不正确的”。这样，模型的目标变为 \[ \begin{align*} &\mathop{ {\rm arg}\max}_\boldsymbol{\theta} \prod_{(w,c) \in D}p(D=1|w,c;\boldsymbol{\theta}) \prod_{(w,c) \in D'}p(D=0|w,c;\boldsymbol{\theta}) \\ = &\mathop{ {\rm arg}\max}_\boldsymbol{\theta} \prod_{(w,c) \in D}p(D=1|w,c;\boldsymbol{\theta}) \prod_{(w,c) \in D'}(1-p(D=1|w,c;\boldsymbol{\theta})) \\ = &\mathop{ {\rm arg}\max}_\boldsymbol{\theta} \sum_{(w,c) \in D} \log p(D=1|w,c;\boldsymbol{\theta}) + \sum_{(w,c) \in D'}(1-p(D=1|w,c;\boldsymbol{\theta})) \\ = &\mathop{ {\rm arg}\max}_\boldsymbol{\theta} \sum_{(w,c) \in D}\log \frac{1}{1+\exp\{-\boldsymbol{v}_c^\mathsf{T}\boldsymbol{v}_w\}} + \sum_{(w,c) \in D'}\log \left(1 - \frac{1}{1+\exp\{-\boldsymbol{v}_c^\mathsf{T}\boldsymbol{v}_w\}}\right) \\ =&\mathop{ {\rm arg}\max}_\boldsymbol{\theta} \sum_{(w,c) \in D}\log \frac{1}{1+\exp\{-\boldsymbol{v}_c^\mathsf{T}\boldsymbol{v}_w\}} + \sum_{(w,c) \in D'}\log \left(1 + \frac{1}{1+\exp\{\boldsymbol{v}_c^\mathsf{T}\boldsymbol{v}_w\}}\right) \end{align*} \] 引入sigmoid符号，则最后目标变为 \[ \mathop{ {\rm arg}\max}_\boldsymbol{\theta} \sum_{(w,c) \in D}\log \sigma(\boldsymbol{v}_c^\mathsf{T}\boldsymbol{v}_w)+ \sum_{(w,c) \in D'}\log \sigma(-\boldsymbol{v}_c^\mathsf{T}\boldsymbol{v}_w) \] 如果引入Mikolov原文构建\(D'\)的方法，并对每个正样本引入\(k\)个负样本，就可以得到前面的目标函数 \[ \log \sigma(\boldsymbol{v}_{w_O}'^\mathsf{T}\boldsymbol{v}_{w_I}) + \sum_{i=1}^k \mathbb{E}_{w_i \sim P_n(w)}\left[\log \sigma(-\boldsymbol{v}_{w_i}'^\mathsf{T}\boldsymbol{v}_{w_I})\right] \] 可以看出，使用负采样的skip-gram模型建模的不是\(p(c|w)\)，而是\(w\)和\(c\)的联合分布。如果固定所有中心词的词向量，只学习上下文的词向量；或者固定上下文的词向量，只学习中心词的词向量，问题都会退化成logistic回归，进而可以使用凸优化方法求解。但是，由于模型中是联合学习两个向量，因此问题是非凸的

频繁词的降采样

在非常大规模的语料库中，某些频繁词（例如“the”、“a”等）可能会出现上百万次，而且这些词提供的信息有限，反而是罕见词传递的信息更多。为了在频繁词与罕见词之间做个平衡，可以使用一种简单的降采样方法，即训练集中的每个单词以概率\(P(w_i)\)被丢弃，其中 \[ P(w_i) = 1-\sqrt{\frac{t}{f(w_i)}} \] 其中\(f(w_i)\)是单词\(w_i\)出现的频率，\(t\)是给定的阈值（通常是\(10^{-5}\)）

GloVe

在word2vec之后，[Pennington2014]提出了一种新式的词嵌入训练方法GloVe（Global Vectors），期望综合两种模型的优点：潜在语义分析模型（latent semantic analysis, LSA）丰富的统计信息，和word2vec隐含的语言学性质（即word2vec可以蕴含king - queen = man - woman的规律）。GloVe背后蕴含的思想是，词与词之间的共现信息不应该被忽视，不应该仅依赖词窗口所传递的知识（word2vec关注的就是一个长度为\(2R\)的窗口），而要把握语料库的全局统计信息

假设单词共现的信息存在矩阵\(\boldsymbol{X}\)中，其中\(X_{ij}\)代表单词\(j\)在单词\(i\)的上下文中出现的次数。令\(X_i = \sum_k X_{ik}\)为单词\(i\)上下文中所有单词出现的总次数，\(P_{ij} = P(j|i) = X_{ij} / X_i\)为单词\(j\)出现在单词\(i\)上下文中的概率。这些共现数据就可以传递很多信息：假设对单词\(i = {\rm ice}, j ={\rm steam}\)，对不同类型的词\(k\)，\(P_{ik}/P_{jk}\)应该不同：

若\(k\)与ice相关但不与steam相关，例如\(k={\rm solid}\)，那么\(P_{ik}/P_{jk}\)会很大
若\(k\)与steam相关但不与ice相关，例如\(k={\rm gas}\)，那么\(P_{ik}/P_{jk}\)会很小
若\(k\)与steam相关也与ice相关，例如\(k={\rm water}\)；或者与两者都不相关，例如\(k={\rm fashion}\)，那么\(P_{ik}/P_{jk}\)会接近于1

由于这种概率比可以很好地找出相关词，而且可以对不同的相关词做出区分，因此词向量学习的切入点应该是共现概率，而不是单词概率本身。因此，模型本身应该满足如下形式： \[ F(\boldsymbol{w}_i, \boldsymbol{w}_j, \tilde{\boldsymbol{w}}_k) = \frac{P_{ik}}{P_{jk}} \] 其中，\(\boldsymbol{w} \in \mathbb{R}^d\)是词向量，\(\tilde{\boldsymbol{w}} \in \mathbb{R}^d\)是上下文词向量。由于\(F\)要能在词向量空间里编码\(P_{ik}/P_{jk}\)所蕴含的信息，而向量空间有线性结构，因此可以使用向量的差，即 \[ F(\boldsymbol{w}_i - \boldsymbol{w}_j, \tilde{\boldsymbol{w}}_k) = \frac{P_{ik}}{P_{jk}} \] 接下来，因为要把向量映射为标量，因此可以直接使用内积，即 \[ F\left((\boldsymbol{w}_i -\boldsymbol{w}_j)^\mathsf{T}\tilde{\boldsymbol{w}}_k\right) = \frac{P_{ik}}{P_{jk}} \] 由于词共现信息矩阵是一个对称矩阵，因此也需要模型有这种对称性。首先要求\(F\)是\((\mathbb{R}, +)\)和\((\mathbb{R}_{>0}, \times)\)两个群的群同构。先回顾一下群同构的概念：给定两个群\((G, \ast)\)和\((H, \odot)\)，群同构\(f\)是双射函数\(f: G \rightarrow H\)使得对\(G\)中所有的\(u\)和\(v\)有\(f(u \ast v) = f(u) \odot f(v)\)。那么，由于\(F\)是群同构，且“在加法群里a减b相当于a加b的逆元；在乘法群里a除以b相当于a乘以b的逆元”，所以有（这里感谢stackexchange的回答） \[ \begin{align*} F\left((\boldsymbol{w}_i - \boldsymbol{w}_j)^\mathsf{T}\tilde{\boldsymbol{w}}_k\right) &= F(\boldsymbol{w}_i^\mathsf{T}\tilde{\boldsymbol{w}}_k - \boldsymbol{w}_j^\mathsf{T}\tilde{\boldsymbol{w}}_k) \\ &= F(\boldsymbol{w}_i^\mathsf{T}\tilde{\boldsymbol{w}}_k + (- \boldsymbol{w}_j^\mathsf{T}\tilde{\boldsymbol{w}}_k)) \\ &= F(\boldsymbol{w}_i^\mathsf{T}\tilde{\boldsymbol{w}}_k) \times F( - \boldsymbol{w}_j^\mathsf{T}\tilde{\boldsymbol{w}}_k) \\ &= F(\boldsymbol{w}_i^\mathsf{T}\tilde{\boldsymbol{w}}_k) \times F( \boldsymbol{w}_j^\mathsf{T}\tilde{\boldsymbol{w}}_k)^{-1} \\ &= \frac{F(\boldsymbol{w}_i^\mathsf{T}\tilde{\boldsymbol{w}}_k)}{F( \boldsymbol{w}_j^\mathsf{T}\tilde{\boldsymbol{w}}_k)} \end{align*} \] 联立上式，有 \[ F(\boldsymbol{w}_i^\mathsf{T}\tilde{\boldsymbol{w}}_k) = P_{ik} = \frac{X_{ik}}{X_i} \] 因此需要\(F\)是指数函数，或者 \[ \boldsymbol{w}_i^\mathsf{T}\tilde{\boldsymbol{w}}_k = \log(P_{ik}) = \log(X_{ik}) - \log(X_i) \] 这里\(X_{ik}\)是对称的，而\(\log(X_i)\)独立于\(k\)，因此可以引入一个偏置\(b_i\)，再引入一个\(\tilde{b}_k\)就能彻底得到对称性 \[ \boldsymbol{w}_i^\mathsf{T}\tilde{\boldsymbol{w}}_k + b_i + \tilde{b}_k = \log(X_{ik}) \] 由于对数函数在\(X_{ik}=0\)时无定义，因此需要加一个小的偏移量：\(\log(X_{ik}) \rightarrow \log(1+X_{ik})\)。考虑\(X_{ik}=0\)时加了偏移量以后对数值为0，因此这样的做法是合理的

这个模型的问题是，所有共现词组的权重都是相等的，但是罕见的共现实际上应该被看做是噪声。如果把之前的模型看作是一个最小二乘问题，并在代价函数中引入一个权重函数\(f(X_{ij})\)，那么可以得到问题求解的最终目标函数 \[ J = \sum_{i,j=1}^V f(X_{ij})\left(\boldsymbol{w}_i^\mathsf{T}\tilde{\boldsymbol{w}}_j + b_i + \tilde{b}_j - \log X_{ij}\right)^2 \] 其中\(V\)是词表大小，\(f\)应该满足如下性质

\(f(0) = 0\)，且当\(x\)接近于0时\(f(x)\)快速接近于0
\(f(x)\)是非减的，使得罕见共现词组不会被给一个过高的权重
\(f(x)\)对太大的\(x\)反而应该较小，因此高频共现词组也不会被给一个过高的权重

经过考量发现\(f\)应该满足如下形式 \[ f(x) = \begin{cases}(x/x_{\max})^\alpha & {\rm if\ }x<x_{\max} \\ {\phantom-\phantom-}1 & {\rm elsewhere}\end{cases} \] 两个超参数的经验值为\(x_{\max} = 100, \alpha=3/4\)

论文接下来讨论了GloVe和word2vec之间的联系，以及算法的复杂度。这里就不做介绍了

词向量的评估

由于词向量的训练本质上是一种无监督的方法，因此需要一些直观有效的方法来对训练出的词向量的效果作出评估。[Schnabel2015]首先做出了这方面比较系统的研究，该文献将词向量的评估方法分成两块，分别是内涵评估和外延评估：

在外延评估（extrinsic evaluation）中，词向量被用作下游任务的输入特征。好的词向量应该对使用其的任务（例如词性标注POSTAG、命名实体识别NER等）有正面影响（但是这种影响为什么存在人们并不是很清楚），但是不同的任务对词向量的偏好可能是不同的，因此也应该为特定的目标训练特定的词向量。此外，使用词向量再为其它任务训练一个模型的时间也比较长，因此外延评估是否有效一直是一个争论点

在内涵评估（intrinsic evaluation）中，可以观察词向量承载了多少词之间语义上的联系。做内涵评估通常需要一个查询库（query inventory），同时需要一些人工标注。[Schnabel2015]对内涵评估分成了两类，但是这两类方法都是为比较不同方法训练出的词向量而设计，尤其是比较评估法是直接让人来选哪种词向量更容易接受，因此这里暂时不做讨论；绝对评估法是对每种词向量单独评估，又可以划分为四项评估方式

相关性（relatedness）：对于一对相关度比较高的词，它们的词向量的余弦相似度也很高吗？这里作为标准的相关度评分由人工给出。其中，文章提出了一种新的方法，称为一致性检查：给出一组单词，看词向量能否找出类别不同的那一个
类比性（analogy）：对给定的词\(y\)，能否找到一个对应的词\(x\)，使\(x\)与\(y\)的关系能够类比另两个已知词\(a\)与\(b\)之间的关系。例如比较经典的king-queen与man-woman之间的关系
类别化（categorization）：对词向量进行聚类，看每个簇与有标记数据集各类相比纯度如何
选择倾向（selectional preference）：判断某些名词是更倾向做某个动词的主语还是宾语，例如一般顺序是people eat而不是eat people

[Bakarov2018] 做了进一步的分类，也是分为四组

有意识评估（conscious evaluation）
潜意识评估（subconscious evaluation）
基于词典的评估（thesaurus-based evaluation）
语言驱动的评估（language-driven evaluation）

其中后三种评估方法或者缺少数据集，或者有点像神经科学/生物学的方法，需要人的配合，很难用代码直接解决，这里就不介绍了。有意识评估方法又可以细分为如下几类

语义相似度。这种做法最常见，但主观性太强，不同人对不同单词对给出的相似度可能不同
类比测试。这种方法的问题是缺乏一个准确的评估标准
主题拟合。对于给定的动词和一个角色，能否找出最符合这个角色的名词？另外一些该类别下的评估方法更像是前面提到的“选择倾向”方法
概念分类，或称为单词聚类。但是聚类问题本身就不太好评估效果
同义词检测。给定一个单词和另一个单词列表，从单词列表中找到与给定单词意思最近的词。这种方法的问题类似于语义相似度的问题，而且评估集的构造更复杂
离群词检测，类似前面提到的“一致性检查”

最后，可以参考GitHub上一套公开的benchmark，这个仓库不仅提供了评估代码，也提供了原始数据集做检查

词向量的陷阱与缺陷

尽管词向量现在得到了非常广泛的应用，但是嵌入表示方法仍然存在一些自身的局限性：

相似性的度量。如前面所述，相似性存在一定主观性。例如，猫、狗、虎这三个词，即可以说“猫”和“狗”相似性更高（因为两者都是宠物），也可以说“猫”和“虎”相似性更高（因为两者都是猫科动物）。嵌入表示法（有时候也称为分布式训练法）并不能控制引入的相似性是哪个层面的
“black sheep现象”。有一些“平凡”的意思并不能在文本中表现出来，因此可能不会被嵌入表示捕捉到。人们在沟通过程中可能更不会去提到已知的信息：当人们提到“white sheep”（败类中的规矩人）的时候，更多倾向于“sheep”传递的意思；当人们提到“black sheep”（害群之马）的时候，更多倾向于“black”传递的意思。这些信息会对词向量造成误导
反义词的处理。反义词出现的语境通常相似，因此分布表示训出的向量可能会导致一组反义词的词向量反而很接近
语料偏见。用来训练的文本里通常会引入一些隐含的偏见，例如欧美人名字可能与褒义词关系更近，而黑人的名字会更偏向于贬义。有时候，把“医生”和“男性”关联和把“护士”和“女性”关联可能是期望的，但是有时候需要消除这种偏见
语境的缺乏。词向量的学习会考虑单词的所有语境，最后学出的向量反而是语境无关的。然而，单词的具体含义往往与语境相关，尤其是当有些单词传递多个意思的时候，例如“bank”

此外，尽管现在有很多开放的、训练好的词向量可以下载，但是仍然建议不要盲目下下来以后当做黑盒使用，因为训练用的语料和其他参数都会对结果造成影响。最好将下下来的结果在验证集上做些实验，同时使用同样的tokenization方法和规范化方法

参考文献

[Britz2017] Britz D, Goldie A, Luong M T, et al. Massive exploration of neural machine translation architectures. arXiv preprint arXiv:1703.03906, 2017.

[Bengio2003] Bengio, Y., Ducharme, R., Vincent, P., & Jauvin, C. (2003). A neural probabilistic language model. Journal of machine learning research, 3(Feb), 1137-1155.

[Turian2010] Turian, J., Ratinov, L., & Bengio, Y. Word representations: a simple and general method for semi-supervised learning. In Proceedings of the 48th annual meeting of the association for computational linguistics (pp. 384-394). Association for Computational Linguistics. 2010

[Mikolov2013a] Mikolov T, Chen K, Corrado G, et al. Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781, 2013.

[Mikolov2013b] Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., & Dean, J. Distributed representations of words and phrases and their compositionality. In Advances in neural information processing systems (NIPS) (pp. 3111-3119). 2013

[Gutmann2012] Gutmann, M. and Hyvärinen, A. Noise-contrastive estimation of unnormalized statistical models, with applications to natural image statistics. The Journal of Machine Learning Research, 13 (pp. 307–361). 2012

[Goldberg2014] Goldberg, Y., & Levy, O. word2vec Explained: deriving Mikolov et al.'s negative-sampling word-embedding method. arXiv preprint arXiv:1402.3722. 2014

[Pennington2014] Pennington, J., Socher, R., & Manning, C. Glove: Global vectors for word representation. In Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP) (pp. 1532-1543). 2014

[Schnabel2015] Schnabel, T., Labutov, I., Mimno, D., & Joachims, T. Evaluation methods for unsupervised word embeddings. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing (EMNLP) (pp. 298-307). 2015

[Bakarov2018] Bakarov, Amir. "A Survey of Word Embeddings Evaluation Methods." arXiv preprint arXiv:1801.09536. 2018