通过堆叠RBM学习特征层
本讲开始,先不提sigmoid信念网(SBN),回过头看看受限玻尔兹曼机RBM。前面提到,学习RBM有一种相对来讲比较简单的方法,可以学出一层非线性特征(隐藏状态)。受此启发,可以将这层特征作为新的输入,再学出一个RBM的非线性特征,如此持续下去,最后可以得到一个由若干RBM堆叠起来的深度网络。但是,这实际上不只是一个简单的多层玻尔兹曼机,Hinton的学生G. Y. Tay指出它实际上是一个深度sigmoid信念网络。可以证明,每次这样添加一层特征,实际上是改善了生成训练数据的概率的对数值的变分下界
假设现在可见向量为\(\bf v\),经过学习,可以得到第一层RBM,其隐藏状态为\({\bf h}_1\),权重为\({\bf W}_1\)。然后,将\({\bf h}_1\)作为输入,学习可以得到第二层RBM,其隐藏状态为\({\bf h}_2\),权重为\({\bf W}_2\)。注意如果\({\bf W}_2\)的初始值为\({\bf W}_1^\mathsf{T}\),且\({\bf h}_2\)的节点数与\(\bf v\)的节点数相同,那么第二个RBM实际上就是\({\bf h}_1\)一个不错的模型,因为它是第一个RBM翻转而成的,而RBM不太在乎哪个是隐藏单元哪个是可见单元。学到这两个RBM以后,可以将它们组合起来得到一个新的模型,它的上面两层是RBM,也就是第二个隐藏层和第一个隐藏层之间是一个无向模型,连接对称;而底下两层(第一个隐藏层和输入)之间是有向模型,像一个SBN。也就是说,对\(\bf v\)和\({\bf h}_1\)之间的对称连接,舍弃那些从\(\bf v\)指向\({\bf h}_1\)的边。这样就得到了一个深度信念网(DBN)。如果DBN由三个RBM堆叠而成,那么最上面两层(沿用前面的记法,是\({\bf h}_3\)和\({\bf h}_2\))形成一个RBM,下面三层形成两个SBN。
对于这样三个RBM堆叠生成的DBN,生成数据的过程是:首先,在\({\bf h}_2\)和\({\bf h}_3\)之间往复运动,达到平衡态(这个过程使用的是交替吉布斯采样方法,即先平行更新所有\({\bf h}_3\)中的神经元,然后平行更新所有\({\bf h}_2\)中的神经元,再平行更新所有\({\bf h}_3\)中的神经元,交替执行这样一个漫长的过程。最后,顶层的RBM实际上定义了\({\bf h}_2\)的先验分布,当这个RBM达到稳态以后,使用\({\bf W}_2\)生成\({\bf h}_1\),再使用\({\bf W}_1\)生成数据。整个结构如下图所示
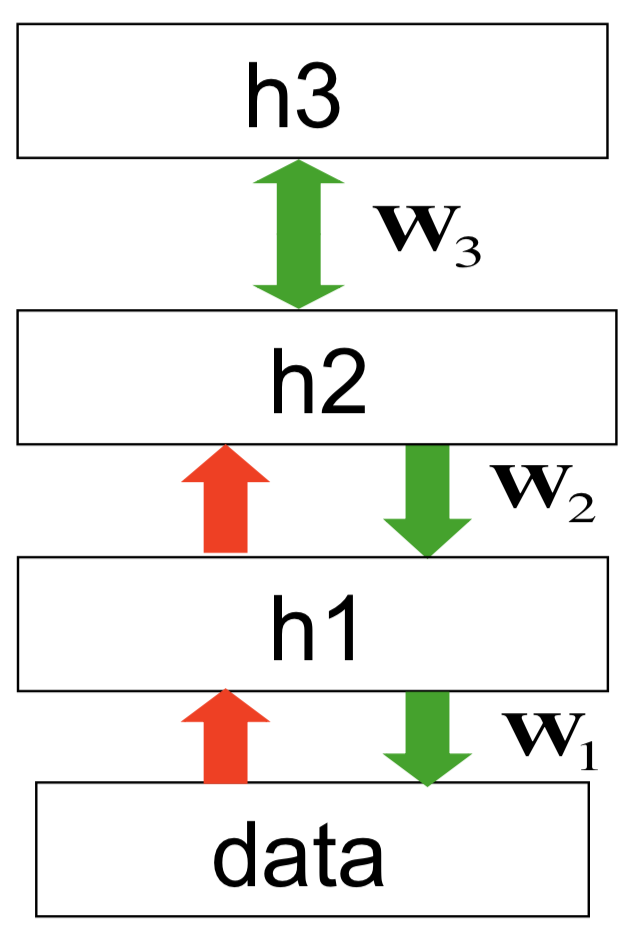
注意这里红色的箭头不是生成模型的一部分,它们是对应\({\bf W}_i\)的转置,在推断时候用到
这里需要插一句的是,阶乘分布的均值不再是阶乘分布。假设RBM有4个隐藏单元,给定一个可见向量,这4个隐藏单元上的后验分布是阶乘的。假设对输入向量\({\bf v}_1\),隐藏单元被打开的概率分别为0.9、0.9、0.1和0.1,对输入向量\({\bf v}_2\),隐藏单元被打开的概率分别为0.1、0.1、0.9和0.9。那么这两个平均(聚合)以后的概率为0.5、0.5、0.5和0.5。现在,假设隐藏单元的状态为(1, 1, 0, 0),如果该状态处于\({\bf v}_1\)的后验分布中,则\(P((1, 1, 0, 0)) = 0.9^4 = 0.6561\)(讲义这里好像算错了……);如果该状态处于\({\bf v}_2\)的后验分布中,则\(P((1, 1, 0, 0)) = 0.1^4 = 0.0001\),在聚合的后验分布下,\(P((1, 1, 0, 0)) = (0.6561 + 0.0001) / 2 = 0.3281\)。但是,如果这个聚合的后验分布也是可分解为阶乘的,那么就应该是\(0.5^4 = 0.0625\)
接下来回到主线:为什么这种贪婪的学习方法(学一个RBM,再学一个新的RBM来对第一个RBM的隐藏单元的行为模式建模)是可行的呢?先学出来的RBM的权重\({\bf W}\)实际上定义了五个不同的分布:前两个是\(P({\bf v}|{\bf h})\)和\(P({\bf h}|{\bf v})\),使用这两个分布可以通过交替马尔可夫链,在给定隐藏状态的条件下更新可见状态,再在给定可见状态的条件下更新隐藏状态。如果这个链运行的时间足够长,就可以获得一个来自于联合分布\(P({\bf v},{\bf h})\)的样本,因此\(\bf W\)也定义了联合分布\(P({\bf v},{\bf h})\)(当然,它也通过\(-E\)的形式更直接地定义了联合分布,但是因为网络里有太多单元,这个值无法计算)。对于这个联合分布,如果忽略\(\bf v\),就得到了\(\bf h\)的分布,也就是由RBM定义的\({\bf h}\)的先验分布。同理,也可以得到RBM定义的\(\bf v\)的先验分布。接下来,定义 \[ P({\bf v}) = \sum_{\bf h}P({\bf h})P({\bf v}|{\bf h}) \] 不看求和项里的\(P({\bf v}|{\bf h})\),只学习一个\(P({\bf h})\)的更好的模型(能更好拟合聚合后验的先验),就也会改进\(P({\bf v})\)的模型(这里聚合后验aggregated posterior指对训练集中的所有\(\bf v\)求\(P({\bf h}|{\bf v})\)的平均)。所以,真正做的事情是,使用第一个RBM来获得这个聚合后验,然后用第二个RBM来为此聚合后验构建一个更好的模型。假设第二个RBM的初始状态就是把第一个颠倒过来,那么初始模型就是第一个RBM所得到的聚合后验,如果调整权重只能让系统更好
将RBM堆叠得到DBN以后,实际上可以对整个系统使用唤醒-睡眠算法的一个变种继续微调(fine-tune):
- 首先,做一个随机的自底向上的计算,调整底层的生成权重,使得底层可以长于重构特征(类似于标准的唤醒-睡眠算法)
- 在顶层的RBM中,做若干次正向和反向的计算,对RBM的隐藏状态和可见状态做若干次抽样,然后做对比差异学习(第12章中所讲述)
- 做一个随机的自顶向下的计算,通过底下的SBN生成数据,进而调整顶层的权重,使得顶层可以长于重构特征(即唤醒-睡眠算法的睡眠阶段)
DBN的一个应用是可以对MNIST手写数字和对应标签的联合分布建模,示意图如下所示
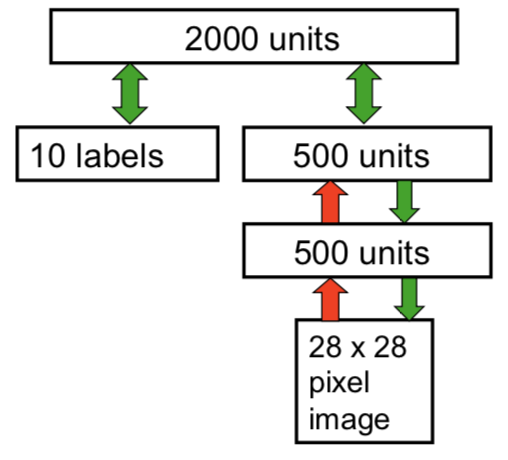
图中,右侧下方由两层RBM堆叠生成的SBN是无监督学习产生的。将最上层的500个隐藏单元和10个标签(实际上是一个softmax单元)连接起来,送入一个大的,有2000个隐藏单元的隐藏层,训练顶层的RBM来对连接向量建模。顶层的RBM训练好以后,用前面介绍的改进版唤醒-睡眠算法微调整个系统,这样整个系统既可以识别数字,也可以很好地生成样本——这也就是导论章节里demo的来源
通过微调使DBN做判别学习
前面说到,DBN的每一层其实都是学习好的RBM,那么连接层与层之间的权重就可以看作是经过预训练得到的权重的初始值。在前一节里,通过唤醒-睡眠算法的一个变种,微调过的权重可以善于生成数据。在这一节,将使用反向传播算法来微调模型,来使它善于判别数据
为什么使用反向传播来微调预训练模型能收到不错的效果呢?对此的解释可以分成两个方面
- 从最优化的方面,如果网络比较大,而且每一层有自己的局部性,那么每一次学习一层效果会比较好。假设现在解决的是计算机视觉的问题,每一层都有一些局部感受野,那么相隔比较远的几块区域不会有什么相互作用,所以并行学出一个很大的层是很容易的。预训练的时候,先学出一些比较合理的特征检测器,然后再进行反向传播,可以让这些特征检测器有助于做判别,因为此时初始的梯度比随机的更合理,反向传播也不需要再做一个全局的搜索
- 从泛化的角度,使用与训练的网络能更好地降低发生过拟合的风险。因为最终学到的权重中包含的信息大部分来自于对输入向量分布的建模,而输入向量(如果做CV)包含的信息通常比标签包含的信息多很多。由于使用预训练模型已经得到了很多特征检测器,就不用再利用标签中包含的信息从头学习了,这些信息已经足够用来把这些检测器微调到类别边界上的合适位置。这里还有一点值得注意,就是因为反向传播已经不再用来发现新特征,因此甚至不需要特别多的有标签数据,使用无标签的数据已经能够发现好的特征了。尽管在没有标签的时候,由于系统不知道学到什么样的特征会对之后的判别任务有帮助,因此会学到比较多无用的特征,但是如果某些特征有用,它们肯定比原始输入有用得多(也就是说,使用生成学习学到的特征肯定有那么几个特别有用,比从头训练一个判别特征要好)
(后面都是讲模型效果怎么好,略)
判别微调时发生了什么
首先,根据Bengio组的工作,第一个隐藏层的特征检测器的感受野在微调前后并没有发生太大的变化,但是效果就是对判别类任务有帮助,而且网络越深,帮助越大。此外,没有经过预训练的网络随着训练epoch的增多,权重最后会陷入不同局部最小值,而有预训练的网络的权重最后相对会集中一些
(上面略去了一些对实验比较具体的讲解)
所以为什么预训练很靠谱呢?假设生成图像-标签对的方式是,让一个现实生活中的人去生成一张照片(例如拍照),然后我们自己去给这张照片根据其像素点的关系贴一个标签,不依赖于拍照的人,那么试图学习一个从图像到标签的映射是合理的,因为此时标签直接依赖于图像本身。但是实际上,更合理也更常见的是,让照片的生成者自己去给生成的图像附加一个标签,那么此时标签就跟图像的生成者有关系,不再跟像素点有关了。而且,照片的生成过程一般是,当你看到一只奶牛,你把它照下来,然后说这张图片是奶牛的图片。因此此时照片的拍摄者和图片之间有很高的带宽,标签不再依赖于图像而依赖于拍摄者,而且两者之间的带宽比较低(不知道这张照片是否被上下颠倒了,不知道奶牛的颜色、死活、大小等等)。因此,比较靠谱的做法是试着先顺着高带宽的通路找到那个拍摄者,再由拍摄者决定标签——预训练的过程,就是从表象追溯本原的过程,而微调的过程就是从本原寻找标签的过程
使用RBM对实数值数据建模
对于手写数字,图片上的某个像素点可能只沾上了一点墨水,因此可以用概率很好地建模——沾上了多少墨水,被激活的概率就是多少。但是对于真实的图像来说,这种做法不会特别奏效,因为真实图片中每个点的像素密度几乎总是它邻居的平均值,这种现象不能用logistic单元建模,它不能表示类似于“像素密度很可能是69,但是不可能是71或67”这样的事实,所以需要另一种单元,通常是用带有高斯范数的线性单元。这样,可以把像素点使用高斯变量建模。对此,仍然可以使用交替吉布斯采样法来运行马尔可夫链,来进行对比散度学习,不过需要设置一个更小的学习率。等式如下所示 \[ E({\bf v}, {\bf h}) = \sum_{i \in {\rm vis}}\frac{(v_i - b_i)^2}{2\sigma_i^2} - \sum_{j \in {\rm hid}}b_jh_j - \sum_{i, j}\frac{v_i}{\sigma_i}h_jw_{ij} \] 右边的第一项是一个向下凹的抛物线,防止能量值过大,其最小值点在第\(i\)个单元的偏置处取到。第\(i\)个单元的值离\(b_i\)越远,能量加得越多,呈二次项关系,因此是要让第\(i\)个可见单元离\(b_i\)尽可能近。第三项表示可见单元和隐藏单元之间的交互项,如果把这一项对\(v_i\)求梯度,可以得到一个常量\(\sum_j (h_jw_{ij}/\sigma_i)\)
能量函数写出来比较容易,也容易求导,但是学习时还是有问题。很多文章都说这种高斯二元RBM很难运转起来,而且也难以学到可见单元比较紧的方差。找到这个问题的原因花了很久,可以参看下图
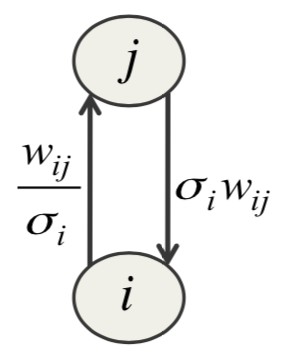
考虑可见单元\(i\)对隐藏单元\(j\)施加的效果,当单元\(i\)的标准差\(\sigma_i\)很小的时候,它会放大自底向上的权重,同时降低自顶向下权重的效果。结果是,或者自顶向上的效果太大,或者自顶向下的结果太小,隐藏单元趋近饱和,要么被永远开启,要么被永远关闭。解决方法是将隐藏节点个数设置得比可见单元数多很多,因此它们之间小的权重也可以有大的自顶向下的效果(人多力量大)
这里,介绍一种单元,称为阶梯sigmoid单元(stepped sigmoid unit)。核心思想史,对每个随机的二元隐藏单元都创造很多拷贝,每个拷贝有相同的权重,也有基本的偏置\(b\),但是对\(b\)施加一些固定的偏移量:第一个单元偏移量为-0.5,第二个-1.5,第三个-2.5,以此类推。这样,如果\(\frac{w_{ij}}{\sigma_i}\)特别小,没有单元被激活,但是随着这个值的变大,被激活的单元数也会线性增多。也就是说,当\(\sigma_i\)变小时,被激活的拷贝单元会变多,使得自顶向下的影响效果不会变小。但是,这种做法代价太昂贵,不过可以做一些快速的近似,有 \[ \langle y \rangle = \sum_{n=1}^\infty \sigma(x+0.5-n) \approx \log(1+e^x) \approx \max(0,x+{\rm noise}) \] 这就是前面提到过的ReLU单元\({\rm ReLU}(x) = \max(0, x)\),计算起来很快
ReLU的一个性质是,如果参数的偏置为0,那么就会有缩放不变性,这种性质对处理图像很好。也就是说如果对图像\(\bf x\),把所有像素密度乘以一个标量\(a\),那么 \[ {\rm ReLU}(a{\bf x}) = a{\rm ReLU}({\bf x}) \] 但是ReLU并不是完全线性的,即 \[ {\rm ReLU}(a+b) \not= {\rm ReLU}(a) + {\rm ReLU}(b) \] 这一性质有点像卷积神经网络展示出来的平移不变性
(14.5节是可选视频,这里跳过了)
