反向传播优劣论
反向传播算法在70年代到80年代被不同的研究组独立发现了几次,不过追根溯源可以到60年代。在1969年,Bryson和Ho在控制论领域发明了反向传播算法的线性版本。Paul Werbos意识到可以将这种算法推广到非线性范畴,并在1974年发表的论文中提出了可能是反向传播的第一个正式版本。1981年,Rumelhart、Williams和Hinton在不知道Werbos的工作的情况下也发明了反向传播算法,但是经过实验没有达到预想的效果,所以就先放弃了。1985年,David Parker和Yann LeCun分别又各自发现了这种算法,Hinton也重新进行了尝试,发现效果不错。1986年,Hinton等人发表了一篇论文,并在文中提出了一个令人信服的例子以说明算法的能力
尽管反向传播算法让人们看到了学习多层非线性特征探测器的希望,但是在90年代末,大部分机器学习界的研究人员都放弃了这种算法。尽管它仍然还受心理学家和实际应用(例如构建信用卡欺诈检测模型)的青睐,但是在机器学习领域,大部分人都认为SVM要更好一些。对此有一些比较流行的解释,比如神经网络不能很好地利用多层非线性特征(CNN是个例外)、RNN和深度自动编码器效果不好,等等。而SVM不需要使用者有太多经验,能产生可复现的结果,还有更好的理论支持,因此当红一时
现在来看,90年代末反向传播不受重视的原因有如下几点:当时的计算机太慢,计算能力太弱,有标签的数据集太少。神经网络太小,也没有得到合适的初始化(一般会初始化太小),因此梯度在反向传播的过程中很容易消失。不过为什么对视觉和语音这样的问题神经网络能获得成功呢?关键问题是,机器学习的任务可以分为两种类型,一种更像统计学界人们研究的问题,另一种是人工智能界人们研究的问题:
| 统计问题 | 人工智能问题 | |
|---|---|---|
| 数据维度 | 低,通常少于100维 | 比较高 |
| 噪声强度 | 噪声多,如何处理很重要 | 噪声不是主要问题 |
| 数据的结构 | 不多,可以被简单模型描述 | 数据中有大量结构,而且比较复杂 |
| 主要问题 | 将真实结构从噪声中剥离。这种问题不适合非贝叶斯神经网络处理,而应该试用SVM或高斯过程 | 找到一种复杂结构的表示方法。适用于反向传播,因为多层神经网络的计算能力很强 |
为什么SVM不适合表示复杂结构呢?总体来看,看待SVM有两种不同的视角。第一种观点是,SVM就是感知机的一个转世化身,只不过应用了一种比较精巧的技巧,即核技巧。这种方法的核心思想是将原始输入映射到一个非常大的非线性、非自适应的特征空间。然后,在这个空间中,学习一个权重。由于使用了最大边界分离超平面法,SVM能用一种有效的方法学习权重,还能防止过拟合。第二种观点仍然把SVM看作是感知机的转世化身,但是对其使用的特征有不一样的角度来思考。在这种观点下,训练集中的每个输入向量都可以用来定义一个“特徵”(原文为pheature。Hinton特意使用了一种不同的拼写方法来区别feature(特征))。每个特徵相当于是对测试输入和这个训练输入做了一次全局匹配,也就是说,定义了测试输入与该训练数据有多相似。然后,有一种很聪明的方法来同时学出如何向这些特徵分配权重来做出正确决策,并同时做特征选择。尽管两个看问题的角度不一样,但是总而言之,SVM都是使用了非适应的特征和一个可适应的权重层——这也就是SVM的限制:你不能使用SVM学出多层表示。一件逸闻是1995年,贝尔实验室自适应系统研究组的老大Larry Jackel和SVM的提出者Vladimir Vapnik打赌。前者赌2000年的时候人们会从理论层面上理解为什么大规模神经网络在大规模数据集上能有良好的效果;而后者打赌在2005年没人会使用反向传播和神经网络。现在看来两个人都错了,限制反向传播训练出的大规模神经网络的根本因素是没有快的电脑和大的数据集,而不是理论基础不完善
信念网
Hinton在20世纪90年代放弃反向传播的一个原因是需要太多有标签的数据集,但是现实生活中很难找到这么多有标签的数据集。但是,使用梯度下降学到权重的方法又比较好,不太让人容易放弃,所以接下来的问题就是能否找到另一种目标函数,可以既使用梯度下降又使用无标签的数据呢?这启发我们使用一种称为“生成模型”的模型,其目标函数是对输入数据建模,而不是预测某个标签。这与统计学和人工智能学界发展出来的新方向图模型相得益彰,这种模型是将离散的图结构组合进来,使用图来表示变量之间的依赖关系,进而可以根据给定的,其它变量的观察值,推出某个变量取值的概率分布。玻尔兹曼机就是一种图模型,不过是无向图模型。1992年,Radford Neal提出可以在玻尔兹曼机的基础上使用有向图,进而提出了sigmoid信念网的概念
深度网络的第二个问题是训练时间太长。当隐藏层很多时,学习过程特别慢。关于这个问题的原因众说纷纭,但是Hinton认为是因为无法找到一个比较合理的权重初始化方法。此外,反向传播算法可能会陷入不太好的局部极值点。如果初始化的随机权重离最优解太远,那么就更容易出现这样的问题。尽管可以使用更简单的模型,然后使用凸优化求解,但是这是一种妥协,逃避了真实数据的复杂度。克服这些反向传播的限制因素的最好方法是使用无监督学习算法,这样做是为了保留梯度下降和SGD的有效性和简洁性,不过是对输入建模,不再对输入和输出之间的关系建模。此时,权重的作用是最大化生成模型生成给定输入的概率,即最大化\(p(x)\)而非\(p(y|x)\)
那么接下来的问题是,应该学习什么样的生成模型呢?是学习基于能量的模型(例如玻尔兹曼机),还是学习由理想化的神经元组成的因果模型呢?还是学习两者的混合模型呢?在讲解因果信念网之前,先来看一下关于人工智能和概率的背景关系:20世纪70年代和80年代早期,人工智能学界的研究人员对概率论有强烈的抵触心态。在那时,如果研究AI的人提到概率,那就会被认为是朽木不可雕,愚不可及,没有摸到AI的门。(中间两段引用略)。进入到20世纪80年代,出现了很多关于专家系统的工作,例如医疗诊断或者矿藏勘探等。这些系统使用了大量的规则,由于要解决实际问题,因此要处理不确定性。由于前面学界共识的影响,大部分AI研究人员仍然不愿意使用概率论作为工具。不过由Pearl、Heckman、Lauritz等人提出的图模型还是拥抱了概率论,并且系统的确比专家系统使用的一个萝卜一个坑的方法要好。具体说来,离散的图可以表示变量之间的依赖关系,而有了图以后,需要做一些计算,来根据给定节点的观察值计算其它节点的期望值。信念网是图模型领域里对某种特殊子图的称呼,这种图是有向无环图,而且连接比较稀疏。在这种情况下,可以有效计算出未观察到的节点的概率。不过这种算法不适合稠密连接的图
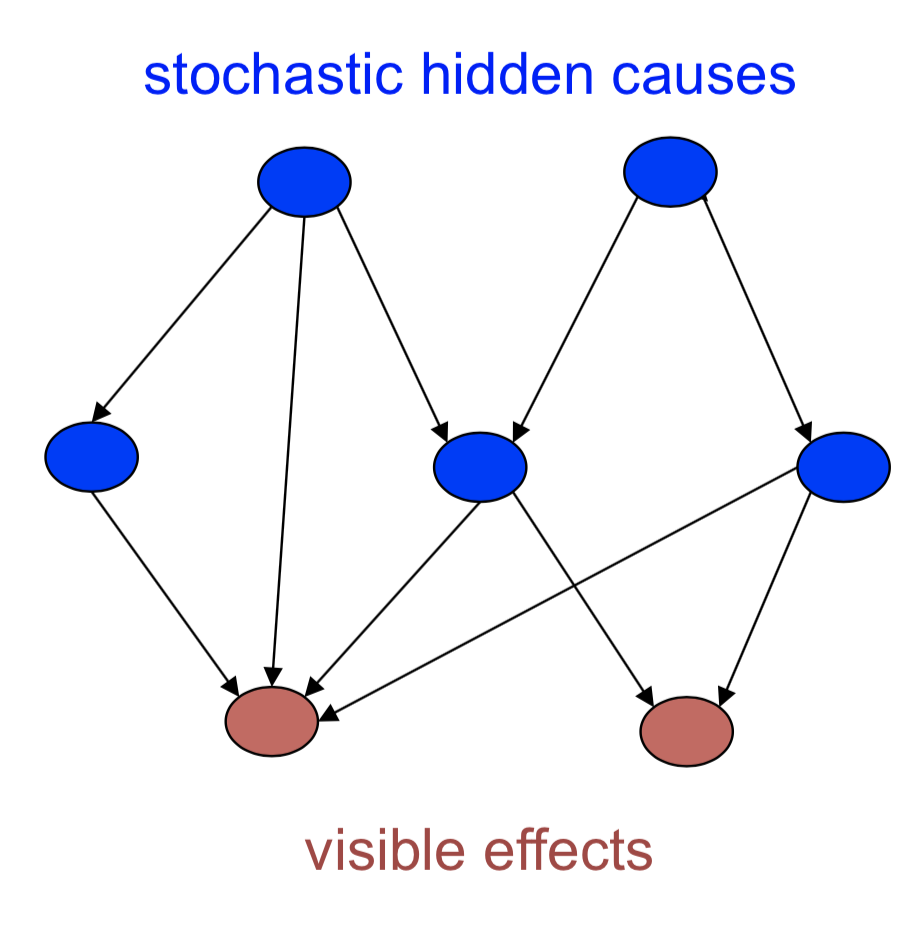
上图给出了一个信念网的示意图。尽管实际可能观察到任何变量,但是这里假设只能观察到叶子节点(没有边流出),即蓝色节点是随机的,隐藏单元;红色的节点是可观察的单元,其中隐藏节点可以看做是可见节点的“因”。当我们观察到变量时,就有两个问题可以解决
- 推断问题:推断隐藏变量的状态(概率分布)
- 学习问题:给定训练集,如何调整变量之间的连接,使得网络更可能生成训练数据?这里对连接的调整包含两项内容:其一是节点之间谁影响谁,其二是这种影响的强度
我们接下来来看一下图模型与神经网络的比较。早期的图模型使用专家来定义(稀疏连接的)图结构和条件概率,因此主要问题是如何正确推断,而不关注学习问题,因为这里隐含了来自于专家的知识。但是对于神经网络,学习永远是核心问题,基本不存在对知识进行硬编码这么一说。尽管CNN里某些基本属性是人工配置的,但是总体来讲,神经网络的知识来源于对训练数据的学习,不是专家的经验。神经网络的目标不是为了提供解释能力,以及稀疏的连接性来让推断变得容易(尽管有神经网络版的信念网)
总体来讲,有两种生成模型可以训练。一种是基于能量的模型,使用对称连接连接器一些二元的随机神经元,这样可以得到玻尔兹曼机。玻尔兹曼机不好训练,但是如果加上对连接性的限制,得到的RBM比较好训练,但是这样只能学习到一个隐藏层,为了训练的容易而放弃了多个隐藏层组成的神经网络的强大能力。另一种是因果模型,是由二元随机神经元组成的有向无环图,也就是sigmoid信念网。1992年,Neal提出了这种模型,并说明其比玻尔兹曼机更容易训练。由于sigmoid信念网的所有神经元都是0-1随机变量,要生成数据,先从最顶层开始,根据偏置值决定这些神经元是0还是1,这样就消除了随机性。得到了第一层的状态,就可以一层层推出下一层的状态,得到一个因果序列,租后就可以得到网络的“信念”,即一个无偏的对可见单元值向量的采样。因此,因果模型比玻尔兹曼机要更容易生成采样结果
(课件中的第三讲“sigmoid信念网的学习”在这次课程中被略去了)
唤醒-睡眠算法
唤醒-睡眠算法(wake-sleep algorithm)是一种有效学习sigmoid信念网的算法,它背后的思想属于一个比较新的机器学习领域——变分学习(variational learning)。这种想法听上去比较疯狂:如果计算正确的后验分布比较难,那么可以算出一些简单的近似值,然后做最大似然学习
给定数据向量的情况下,学习诸如sigmoid信念网这类的复杂模型是比较难的,因为很难从隐藏配置的真是后验分布上取样,不好获得无偏的取样样本。所以一种疯狂的想法是,从某些其它分布取样,然后希望学习过程能正常进行。我们假设隐藏配置上的后验分布能被分解为每个独立隐藏单元分布的连乘,也就是说,假设数据已经给定,每个隐藏层单元都相互独立。这种假设在RBM中是正确的,但是在sigmoid信念网中是错误的
来快速看一下这种“阶乘分布”的例子。假设我们有三个隐藏单元,各自被激活的概率是0.3、0.6和0.8,那么隐藏状态为(1, 0, 1)的概率就是\(0.3 \times (1-0.6) \times 0.8 = 0.096\)。通常情况下,长度为\(N\)的二值向量的自由度是\(2^N\)(实际上是\(2^{N-1}\),因为概率值相加必须为1),但是阶乘分布的自由度只有\(N\)
接下来来看一下分解-睡眠算法。在该算法里,神经网络有两套权重,如图所示
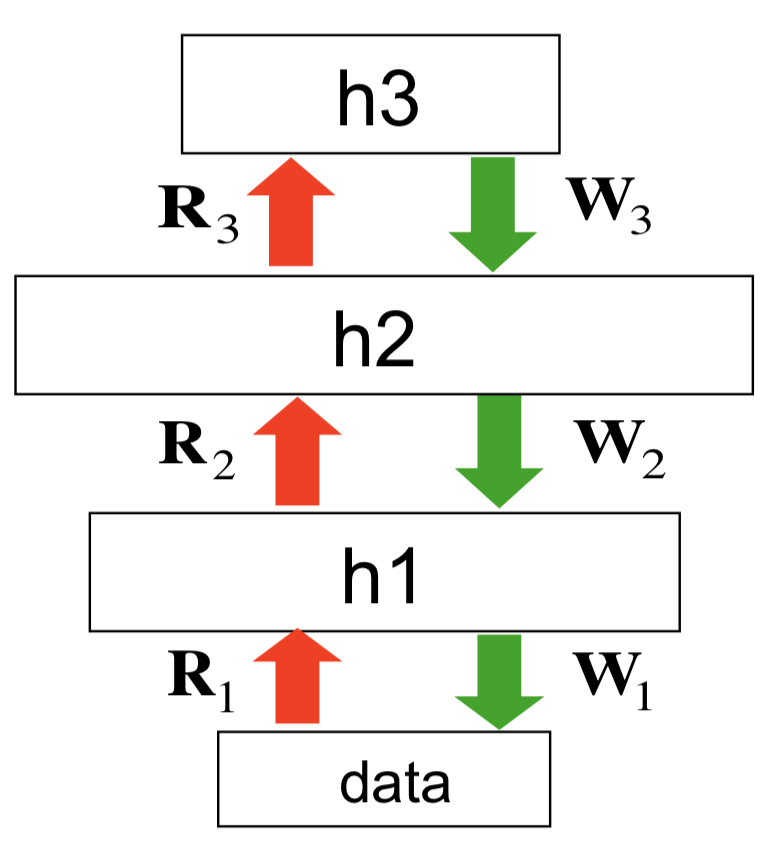
模型本身是一个生成模型,因此绿色箭头是模型本来的权重,称为生成权重(generative weights),用来定义数据向量上的概率分布。此外,还有一些额外的权重,称为识别权重(recognition weights),以红色箭头表示。这些权重用来获得后验分布的近似值,即用来获得每个隐藏层的阶乘分布以(不是很好地)逼近后验分布。如算法名称所示,算法分成两个阶段:
- 唤醒阶段。在这个阶段,把数据放在可见层(最底层),然后使用识别权重做一个前向传播。在每个隐藏层,独立为每个隐藏单元做一个随机的二项决策,决策是应该打开还是关闭。所以,前向过程可以得到所有隐藏单元的随机二元状态,我们将它看作是从给定数据的情况下真实后验分布中的一个取样,并用它来做最大似然学习,不过学习的是生成权重
- 睡眠阶段。在这个阶段,做的事情都反了过来:在顶层,生成一个随机向量,根据隐藏单元的先验分布独立生成状态,然后一路走下来,每次生成一层的状态,最后生成模型的一个无偏抽样。拿到这个抽样以后,就可以看是否可以从数据恢复隐藏状态,也就是说,在这个阶段,使用生成权重做传播计算,学习识别权重
尽管实践上看,如果权重是随机初始化的,那么经历过几次唤醒-睡眠阶段的切换,能学习到一个很好的模型,但是算法仍然有瑕疵
- 识别权重学的是把生成模型“反过来”。但是在学习的开始阶段,它们是在没有任何数据的空间里学着吧生成模型反过来。因为最开始使用模型生成数据时,权重不好,生成的数据与真实数据相比差别很大。所以这是一种浪费——当然咯,这是个小问题
- 识别权重并不遵循数据对数概率的梯度,甚至也不遵循该概率变分界(variational bound)上的权重。由于没有遵循正确的梯度,因此会得到错误的模式平均(mode averaging)——这是个严重的问题。模型平均的概念下文会解释
- 我们知道,由于相消解释作用(explaining away effect),最上面的隐藏层上的真实后验分布远非独立的,但是为了简单起见,我们假设分布独立。不过这种近似估计对中间的隐藏层可能不是一个很差的选择
尽管如此,Karl Friston认为这就是大脑工作的原理,但是Hinton认为应该还有更好的算法
最后来看一下模式平均。不过这里,笔者补充一个来自于原先13.3节中的例子,这个例子在讲模式平均时用到了,而且还可以用来对相消解释作用做说明。所谓相消解释,指的是即便两个隐藏状态(可以看做是事件发生的原因)在先验上是独立的,当我们观察到它们都能影响到的某件事的结果时,这两个原因也变得彼此相关了。例如,无论是卡车撞到房子还是发生地震,房子都会产生剧烈的抖动,而且发生地震和卡车撞击两件事是独立的。但是如果我们发现房子抖动了,而且观测到了地震,那么“发生了卡车撞击”这件事的概率实际上降低了。现在再来看这个例子,如下图所示
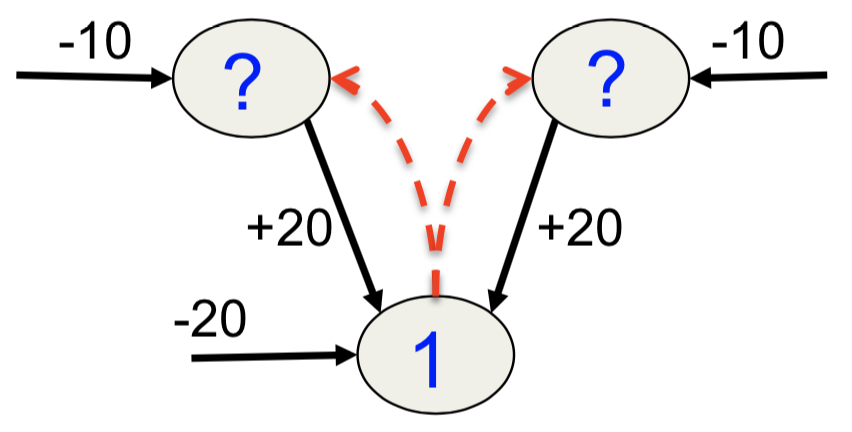
假设首先运行睡眠阶段的算法,通过模型产生数据,大多数情况下,顶部的两个单元都是关闭的,因为按照先验分布两件事发生的概率不大。因为它俩是关闭的,而且可见单元的偏置是-20,因此可见单元也是被关闭的。假设在很偶然的情况下(大概十亿分之一)两个隐藏单元中的一个被打开(两者被打开的概率相等),那么可见单元有一半的可能性会被打开。换句话说,如果看到可见单元被打开,那么有一半概率是左边的隐藏单元被打开,另一半是右边的被打开,但几乎不可能是两个都被打开或被关闭。那么来看看识别权重会学到什么:一半情况下,可见单元被置为1,两个隐藏单元被激活的概率相等,因此两者的概率都是0.5。最后,识别单元会在隐藏层上学习生成一个对(0.5, 0.5)的阶乘分布,最后会是有1/4的概率得到配置(1, 1),另有1/4的概率得到配置(0, 0),但是这两者在可见单元被激活时都是很不可能的配置。实际上,最好的识别模型是只选择一个模式,例如只打开左边或只打开右边
