(视频和讲义中的第二节“More efficient ways to get the statistics”由于是可选章节,被略去了)
玻尔兹曼机学习
玻尔兹曼机学习算法不是一个有监督学习算法,没有期望输出。给定一个输入向量(实际上更应该是看做输出向量),算法试图构造一个模型,模型会为训练集中每个二进制向量计算一个概率,而学习的目标是让这些概率的乘积最大化,也就是让概率的对数和最大化。此外,这个概率也是通过如下方式得到训练集里所有\(N\)条训练数据的概率:令网络在没有外部输入的情况下进入稳定状态,对可见向量做一次抽样,如此重复\(N\)次
玻尔兹曼机的学习过程是比较难的,这里以一个简单模型来做一个示例。模型结构如下图所示
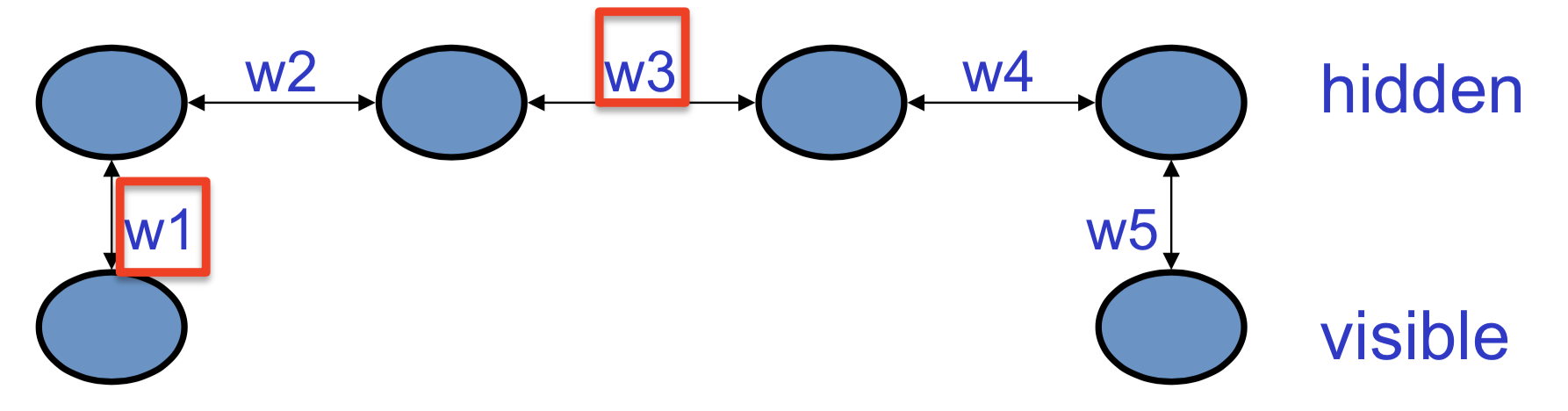
这里,四个隐藏单元链式相连,两端各自接一个可见单元。给这个网络的训练集是(0, 1)和(1, 0),也就是说,我们希望两个可见单元处于各自相反的状态——这就要求所有权重的乘积为负。因为,比如说所有权重都是正的,让\(w_1\)为正就会让第一个隐藏单元为正,这会使第二个隐藏单元也为正,以此类推,因此第四个隐藏单元会让另一个可见单元也为正
(这里我试图展开一点来讲这个事情。由于前面学得不是太扎实,因此可能存在偏差。如果我的想法的确有问题,请及时纠正我!
在前一讲,有一个给定可见单元配置\(\bf v\)和隐藏单元配置\(\bf h\)时整个网络能量的计算公式,为 \[ -E({\bf v},{\bf h}) = \sum_{i \in {\bf v}}v_ib_i + \sum_{k \in {\bf h}}h_kb_k + \sum_{i< j}v_iv_jw_{ij} + \sum_{i,k}v_ih_kw_{ik} + \sum_{k<l}h_kh_lw_{kl} \] 这里没有截距,可见单元之间也没有权重连接,因此可以简写为 \[ -E({\bf v}, {\bf h}) = \sum_{i,k}v_ih_kw_{ik} + \sum_{k<l}h_kh_lw_{kl} \] 为了让这个式子尽可能大,给定\(v_1\)和\(w_{11}\)都为正,那么\(h_1\)应该为正。由于\(w_{12}\)也为正,那么\(h_2\)为正才能使\(h_1h_2w_{12}\)为正。这样推导下去,在\(v_1\)为正且所有\(w_{ij}\)都为正的情况下,\(v_2\)也应该为正才能是能量最大化)
如果把其中某个权重变为负数,那么就可以得到两个隐藏单元之间的反相关关系。这意味着学习\(w_1\)的时候要知道其他权重,例如要想知道如何修改\(w_1\)就要知道\(w_3\)的值,因为\(w_3\)为正的时候对\(w_1\)的修改和\(w_3\)为负的时候对\(w_1\)的修改是不一样的。不过这种看似复杂的情形实际有一种很简单的学习算法,而且这种算法只需要局部信息。实际上,任意权重对其它所有权重和数据要了解的内容都包含在两个相关性的差里。或者换种方式说,如果将玻尔兹曼机给某个可见向量\(\bf v\)的概率的对数值\(\log p({\bf v})\),对权重\(w_{ij}\)求偏导数,其等于如下两者的差 \[ \frac{\partial \log p({\bf v})}{\partial w_{ij}} = \langle s_is_j\rangle_{\bf v} - \langle s_is_j \rangle_{\rm model} \] 其中
- \(\langle s_is_j \rangle_{\bf v}\)是将可见单元限制为\(\bf v\),当系统进入热平衡状态时,状态乘积的期望值
- \(\langle s_is_j \rangle_{\rm model}\)是不对可见单元做限制,当系统进入热平衡状态时,状态乘积的期望值
将第一项命名为\(\langle s_is_j \rangle_{\rm data}\),可以得到 \[ \Delta w_{ij} \propto \langle s_is_j \rangle_{\rm data} - \langle s_is_j \rangle_{\rm model} \] 第一项说明表示数据时,增加权重的量等比于活动单元状态的乘积;而第二项则用来加以控制,当你对模型分布做采样时,它降低权重的量等比于两个单元一起被激活的频率。可以如此理解:第一项对应于Hopfield网的记忆存储,第二项对应于避免陷入伪最小值点——这条规则其实是在说明“忘却”(unlearning)过程是如何进行的
那么为什么这个偏导数的形式如此简单呢?热平衡是全局配置的概率是能量的指数函数,即\(p \propto e^{-E}\)。所以当达到热平衡时,可以得到概率对数与能量函数的一个线性关系。由于能量函数与权重也是线性关系,因此权重和概率对数是线性关系,所以有 \[ -\frac{\partial E}{\partial w_{ij}} = s_is_j \] 实际上,系统最后稳定到热平衡的过程就是传播权重信息的过程。这里不需要一个显式的反向传播,而是要分成两个阶段:有数据情况下的稳定阶段和无数据情况下的稳定阶段。不过网络在这两个阶段的行为基本类似,只是边界条件不一样(如果用反向传播算法,正向传播的计算过程和反向传播的计算过程完全不同)
为什么要有一个无数据情况下的稳定阶段(这里称为负向阶段)?前面提到这就像Hopfield网避免陷入伪最小值点的忘却过程,不过这里稍作进一步解释:对于某个可见向量,其概率可以写为 \[ p({\bf v}) = \frac{\sum_{\bf h}e^{-E({\bf v}, {\bf h})}}{\sum_{\bf u}\sum_{\bf g}e^{-E({\bf u}, {\bf g})}} \] 看分子(正向阶段,注意这里“正向”对应的是英文的“positive”),其实是降低求和项里能量大的项,使得系统在可见单元已经为\(\bf v\)的情况下,到达热平衡时可以找到适合\(\bf v\)的隐藏向量\(\bf h\),从而使\(\bf v\)的能量足够小。调整权重的过程实际上是让分子变大,能量变小的过程。学习的第二个阶段是对分母(划分函数)做同样事情的过程。对于其它能让系统能量比较低的全局配置(其实是可见状态和隐藏状态的组合),算法试图提升它们的能量。也就是说,正向阶段是增大分子,负向阶段是减小分母
为了将这些学习规则跑起来,需要收集统计信息,包括正向统计信息和负向统计信息两种。一种比较基本、效率低下的方法是:
- 在正向阶段,将可见单元设置为数据向量,然后将隐藏单元设为随机的二元状态。每次更新网络中的一个隐藏单元,直到网络达到温度为1的热平衡。然后,对每对相连的单元,抽样求\(s_is_j\)的期望。将这个过程应用于训练集里的每条数据,然后求均值
- 在反向阶段,不做任何限制,将所有单元设为随机二元状态,然后每次更新一个单元,直到网络达到温度为1的热平衡。然后,对每对相连的单元,抽样求\(s_is_j\)的期望。重复以上过程很多次
现在的问题是,在反向阶段,究竟要重复前述操作多少次(后面大概说了一下,但是最后也没说清需要采样多少次……)
以上介绍的是一种比较低效的收集统计信息的方法。更高效的方法是可选内容,这里不做介绍
受限玻尔兹曼机(RBM)
受限玻尔兹曼机(RBM)对普通玻尔兹曼机施加的限制有两点:一是隐藏层只有一层,二是隐藏单元之间没有连接(所以画出来的图是一个二部图),因此给定可见单元的情况下,可以很容易得到平衡分布(原因是隐藏节点相互独立)。这使得RBM的学习过程和推断过程都很容易——给定可见单元的向量以后,一步就可以达到热平衡。即给定可见单元向量以后,可以计算出每个隐藏节点\(h_j\)被激活的概率,进而计算\(v_ih_j\)的期望值(其中\(v_i\)是某个可见节点)。其中\(h_j\)被激活的概率为 \[ p(h_j = 1) = \frac{1}{1+\exp\{-\left(b_j + \sum_{i \in {\rm vis}}v_iw_{ij}\right)\}} \] 由于该值独立于其他所有隐藏节点,因此可以把这个概率并行求出。如果训练集里有多条数据,可以使用Tieleman在2008年给出的PCD算法。算法仍然分为两个阶段
- 正向阶段:对每条数据,将可见单元设置为给定的向量,计算所有隐藏节点和可见节点对的\(v_ih_j\)。对所有相连的节点对,\(\langle v_ih_j \rangle\)是mini-batch上所有数据的平均值
- 负向阶段:准备一些“幻想粒子”(fantasy particle),这些幻想粒子实际上是一些全局的配置。然后,对每个幻想粒子,做几次如下的“交替并行更新”:每次更新权重以后,对幻想粒子也做一点更新,把它们往平衡态拉一点。对每对连接的单元对,求所有幻想粒子的平均\(v_ih_j\),得到负统计数据
这个算法能达到不错的效果,而且允许RBM构建密度比较好的模型。不过,还有一种更快的学习算法。在此之前,先看一种效率比较低的学习算法:在最开始的时候,将可见单元设为一条训练数据,称此时为\(t_0\)时刻。给定可见单元以后,更新隐藏单元,可以算出\(t_0\)时刻状态乘积的期望值,记为\(\langle v_ih_j \rangle^0\),与\(t_0\)对应。得到新的隐藏单元以后,返回来并行更新所有可见单元,得到\(t_1\)时刻的可见单元,再并行更新所有隐藏单元,得到\(\langle v_ih_j \rangle^1\),从而完成一次重构过程。在漫长的往复更新以后,在第\(\infty\)时刻,系统达到热平衡,按照上面的记法,可以得到\(\langle v_ih_j \rangle^\infty\)。此时得到了幻想粒子。接下来学习规则就比较简单了,为 \[ \Delta w_{ij} = \epsilon(\langle v_ih_j \rangle^0 - \langle v_ih_j \rangle^\infty) \] 这个算法的问题是要运行太久的时间才能达到热平衡,得到幻想粒子。令人惊愕的是,实际上只需要走一步(更新两次隐藏单元和一次可见单元),就可以获得需要的统计值,然后使用如下方法更新权重 \[ \Delta w_{ij} = \epsilon(\langle v_ih_j \rangle^0 - \langle v_ih_j \rangle^1) \] 这种做法肯定不是最大似然法,因为负统计数据是错的,不过这种方法在实践中可用。这是为什么呢?马尔可夫链会以给定数据为起点开始向着平衡分布游走,因此经过少数几步以后就可以看到游走的方向。如果初始权重不好,走到平衡态实际就是浪费时间。我们不用等系统进入平衡态就能知道如何修改权重来防止它走到错误的方向,要做的就是降低在完整一步之后生成“虚构(confabulation)”的概率,提升数据的概率,这样模型就不会走错了。一旦数据和模型走了完整一步以后达到的区域有相同的分布,学习过程就会停止
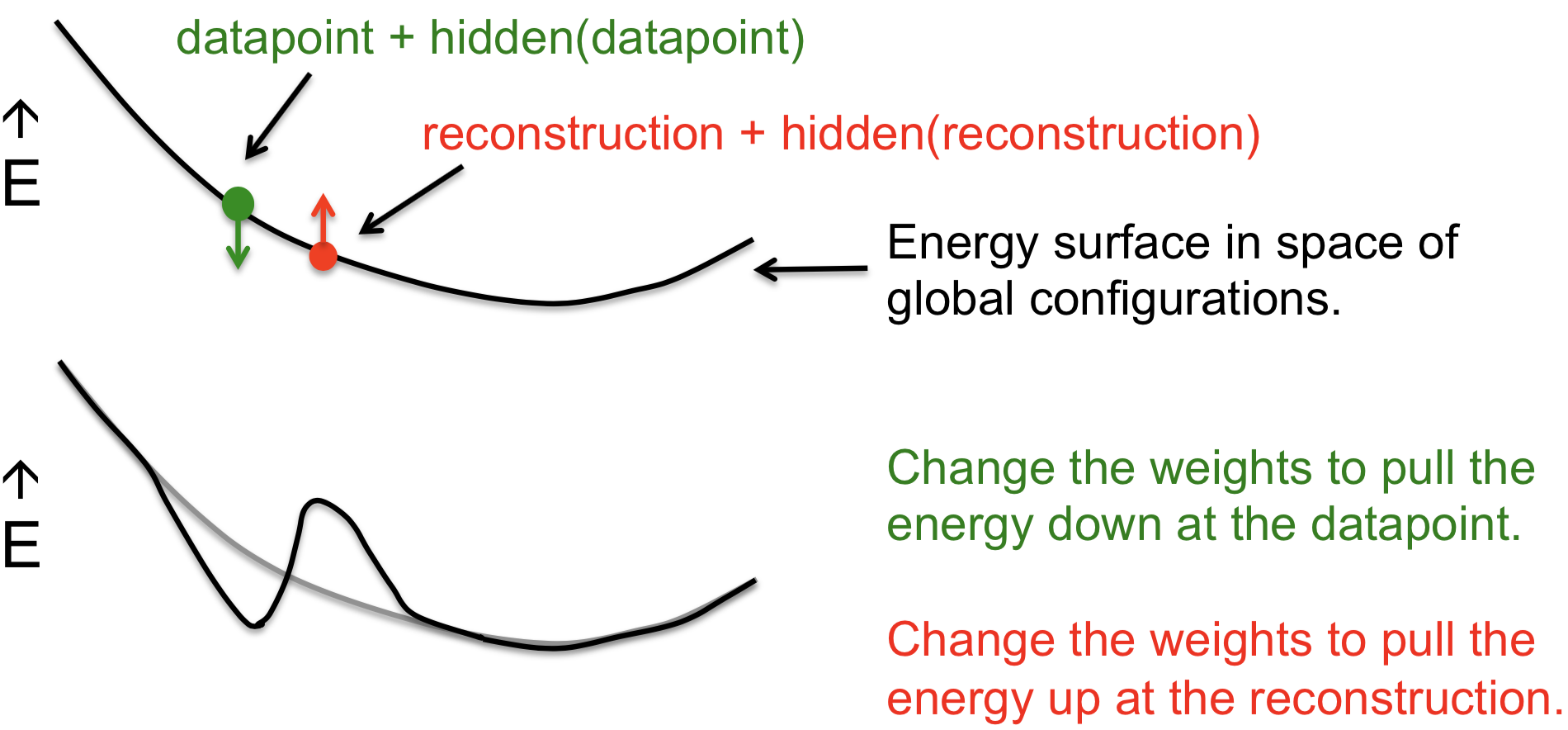
这里给出了一个全局配置空间中的能量表面示意图,用以解释前面介绍的“对比差异学习算法”(contrastive divergence learning,又称为对比散度学习)。绿色的点是一个数据点,也就是可见向量和通过随机更新隐藏单元得到的隐藏向量。从这个点开始,让马尔可夫链经过一个完整的更新步骤,可以得到新的可见向量和相对应的隐藏向量,也就是红色的重构点。然后,修改权重会降低数据点的能量,增大重构点的能量,得到一个经过局部拉伸的新表面。可以看到这样实际上是在数据点创建一个能量最小值,同时让远离数据点的部分保持不变
因此,这种取巧做法对远离数据点的部分会失效,我们需要小心那些里数据空间很远,但是模型很喜欢的区域。这些低能量的孔洞可以导致正则项变得很大,而且如果使用上述取巧法无法感知到。如果使用持久粒子(即它们的状态会被记忆,而且在每次更新以后会被多次更新),这些粒子会找到这些孔洞,掉进去,学习过程变成补洞的过程。所以,更平衡的方法是先使用一些小的权重,然后以CD1算法开始(在一次完整的步骤之后就获取负统计数据),过一段时间,变成使用CD3,再过一段时间,使用CD5……以此类推
RBM学习示例
本讲介绍如何使用RBM学习一系列特征,以重构手写数字2的图像。输入图像是16像素 x 16像素的,有50个二值的隐藏单元来学习特征。接收到数据的时候,先使用权重和节点之间的连接激活特征(也就是对每个隐藏神经元,使用随机决策来看它是否应该被激活),然后使用这些特征重构数据(对每个像素,判断是否应该为1),最后使用重构数据重新激活特征。当网络观察原始数据时,增加活跃像素和活跃特征探测器(隐藏单元)之间的权重,降低原始数据的全局配置的能量;当网络观察重构数据时,减小活跃像素和活跃特征探测器之间的权重,增加重构数据的能量。在学习刚刚开始,权重都随机(使用随机权重来打破网络的对称性)的时候,重构的能量几乎肯定比原始数据的要低,因为重构数据是网络在给定隐藏单元激活状态时倾向在可见单元上产生的值,而它肯定会根据能量函数产生低能量的数据。学习的过程就是降低原始数据能量,提高重构数据能量的过程 (后面学习过程和效果略。大致来说,对没见到的图像,网络可以给出一个不错的重构数据。由于网络把什么都看作是数字2,如果给进一个3,它也会试图重构出一个像2的图像,保持顶部形状不变,但是中间弯折的部分会处理出比较模糊的效果)
使用RBM做协同过滤
(协同过滤的背景略)
可以训练一个“语言模型”,也就是把每条数据写成一个三元组组成的字符串,形式为<用户名 电影名 评分>。这样一来,推荐系统就是要根据元组的第一、二个元素猜测第三个元素是什么。因此可以将每个用户编码成一个向量特征,每个电影也编码成一个向量特征。将这两个向量特征求内积,就可以得到预测的评分(甚至都不用做softmax)。这种模型实际上称作矩阵分解模型,因为如果把用户向量按行排列,电影向量按列排列,就会得到两个矩阵。如果将这两个矩阵相乘,就会得到所有的得分
另一种方法是使用RBM来解决这个问题,但是看上去不那么直观,需要绕一下。假设把每个用户看成是一条训练数据,表现为由电影评分组成的向量,而对每部电影建立一个可见单元,每个单元有五种可能取值(因此可见单元不再是二元的,而是五路softmax得到的结果)。因此网络里有约18000个可见单元,此外还有约100个隐藏单元,每个单元只有0或1两种取值,还带有一个偏置项。由于用户不可能看过所有电影,因此模型要做的事情是预测缺失值(对用户没看过的电影,猜测用户会打多少分)
这里面的隐忧是,网络里如果有18000个可见单元,又要求每个可见单元都与所有隐藏单元全连接,网络的权重数太多了。但是,由于每个用户点评过的电影都只有少数若干个,因此实际可以对每个用户维护一个不同的RBM。这些不同的RBM的可见单元不同(对应于用户评过分的电影),但是隐藏单元都共享,而且从每个隐藏单元到每部电影的权重也被所有为这部电影打过分的用户共享。训练的时候,先使用前面的CD1,过一段时间改为CD3,然后是CD5和CD9。使用RBM解决协同过滤取得的效果跟矩阵分解的总体效果差不多,但是两者犯的错误很不一样。因此同时训练两个模型,然后对模型求平均可能会收效很大
