学习预测下一个单词
本讲将介绍反向传播算法的一个有趣的应用,即可以用它来学出对单词意义的一种特征表示。这种做法可以追溯到20世纪80年代,那时人们使用神经网络来理解家族树(family tree)中所包含的信息。下图给出了家族树的一个示意图
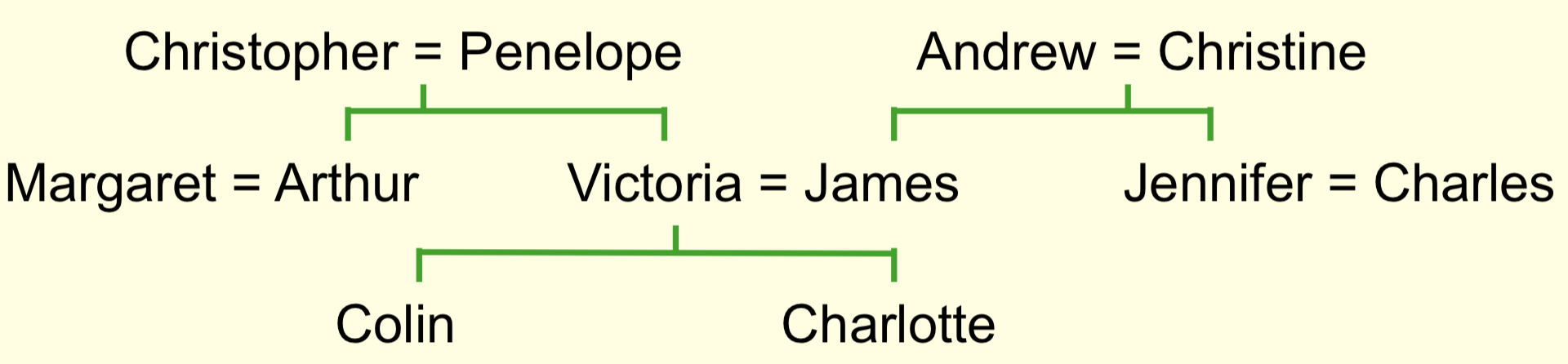
家族树中包含了大量的人名,同时可以定义一些谓词来表示这些人之间的关系,包括父子关系、夫妻关系、叔侄关系/姑侄关系等等。其中,在给定了某些关系的前提下,一些关系可以推导出来。例如: \[ ({\rm colin}\ has{\text{-}}father\ {\rm james}) \land ({\rm colin}\ has\text-mother\ {\rm victoria}) \rightarrow ({\rm james}\ has\text-wife\ {\rm victoria}) \] 因此,具体的学习问题就是,给定大量表示家族树中信息的元组,学习出这些谓词之间的关系。最简单的办法是手写这些规则,但是这样会使得搜索空间变得很大,因此研究人员试图让神经网络在一个由实数权重组成的连续空间中搜索并捕捉信息。如果送给神经网络一个人名和一个关系名称,它能够给出对应的人名,那么就说这个神经网络学成了。例如,对上面的例子,神经网络的输入如果是James和wife,它应该能输出Victoria
设计的时候,网络的输入层对人名和亲属关系都进行了独热编码。对每条数据, 只有两个神经元被激活,分别对应一个人名和一个关系。而输出是24个神经元,对每条数据只有一个神经元被激活。使用独热编码的好处是,对这24个向量组成的集合,其任何子集中的向量都是线性无关的,而且不需要对每个人名有任何先验知识
接下来,对人名部分,会有6个神经元与之相连。因为这一层的神经元数小于输入层神经元数目,因此每个神经元不可能只对应于一个人名。这样,神经网络需要把每个人名表示成这6个神经元的某种行为模式。换句话说,这一层实际上可以学出来每个人名的分布式编码(输入的独热编码则对应地被称为局部编码)
学习到的结果如下图所示

这里一共有6个灰色块,对应着6个神经单元。每一个灰色块里包含了24个大小不一的黑白色块,其中大小表示了权重的绝对值大小,黑色表示负值,白色表示正值。每个灰色块里的第一行对应于英语人名,第二行对应于意大利语人名。图中已经给出了各个英语人名分别对应于第几个色块
从图中可以发现一些学习到的有趣事实
- 右上角的灰色块中,英语人名的权重都是正的,意大利语人名的权重都是负的(第一行都是白的,第二行都是黑的),这说明对于给定的名字,神经网络可以判断其是属于哪种语言。因此对给定英语的输入,它断不会给出意大利语的输出
- 第二行右边灰色块中,有四个大的白块,对应于英语的Christopher, Andrwe, Penelope和Christine(以及意大利语的相应人名);而两个大的黑块对应于英语的Colin和Charlotte(以及意大利语的相应人名)。这里值的符号可以理解为,大的正值意味着人的辈分高,而小的负值(绝对值大的负值)意味着人的辈分低,中坚一代则是在0附近波动。即这个神经元反映了辈分信息
- 第三行左边的灰色块中,Andrew、James、Charles、Christine和Jennifer(甚至包括Charlotte)都是负值,对应于家族树中,这些人都来自树的右侧。也就是说,模型可以学出给定的人来自树的哪一支
令人兴奋的是,以上信息都没有被人编码在数据里,而是由神经网络根据给定数据自己学出,它能自动判定在这个领域里哪些特征是好的特征。当然,这些特征起作用的先决条件是其它信息(例如亲属关系)使用相似的表现形式,以及后面的隐含层能够学到如何使用这些特征预测其它特征
另一种观察神经网络如何工作(以及对其工作进行评估)的方法是,对已有的112条关系随机选出108条来训练,然后看神经网络在剩下4条数据上的表现。这项在20世纪80年代进行的实验最后能得到50%到75%的准确率,对于一项24分类的任务来说,这个结果已经足够可喜可贺,而且如果训练集更大,效果应该会更好
如今,我们有更大的数据库,里面可能有百万条的关系数据,每条数据都可以写成\(A\ R\ B\)的形式(即\(A\)与\(B\)存在关系\(R\))。对于这样的数据,可以训练两种网络
- 一种网络是前面介绍的原型的延展,也是接受\(A\)和\(R\)做输入来预测\(B\),这样可以找到数据库中不太可能出现的元组,即对已有数据进行纠错
- 另一种类似,但是是接受\(A\)、\(R\)和\(B\)做输入,并为这些输入打标记,0为不可能,1为可能,以此来预测某个三元组为真的概率
对家族树例子的简明神经科学解释
本节可能会引起科研人员的兴趣,但是估计不合工程人员的胃口。因此如果你是工程师,可以跳过本节:)
在计算机科学圈子里,有一项争论估计持续了将近一百年,就是概念应该是用一个特征向量来表示,还是用其与其他概念之间的关系所表示
- 特征学派认为,概念实际上就是语义特征组成的一个大集合。这样的定义有助于解释概念之间的相似度,而且对机器学习很方便
- 结构主义理论认为概念的意义寓藏于其与其它概念的关系之中,因此概念知识最好表示为关系图,而不是向量
Hinton认为这两派都错了,因为它们认为这两者是你死我活的,但实际关系并不是这样,比如神经网络就是使用语义特征向量来实现关系图。前面那一小节已经证明,神经网络可以在不给定推导规则的前提下,根据给定的人名和关系,通过一遍正向传播的计算就可以找出对应的人名,其原理是许多概率特征互相影响。这种特征一般被称作“微特征”,来强调说它们并不是显式的,有意识的特征。就像大脑一样,大脑有上百万个神经元,神经元之间还有上百万个交互,因此有的时候人可以“扫一眼”就得出结果。这中间可能没有有意识的思维过程,但是这也是神经元之间通过交互大量计算得到的结果。有时候,人可能会使用一些外在的规律来做一些有意识的、细致的推导,但是有时候也会凭直觉,下意识的思维来做事情
有很多人在考虑如何使用神经网络实现关系图的时候,通常假设一个神经元代表关系图中的一个概念,神经元之间的连接表示一个二元关系。不过这种想法一般不能实用,因为现实中“关系”可能有很多种形式,而神经网络中神经元的连接只有大小,没有类型之分,而且这样也不方便表示三元关系。真正应该怎么使用神经网络来实现关系图还没有一个公认很好的解决方案,但是很大可能是用多个神经元表达某一个概念,而且每个神经元会用来参与表示不同的概念。这种表示法就称为概念的分布表示,也就是说,概念和神经元之间的关系是多对多的
softmax输出函数
softmax输出函数会让神经网络的输出之和变为1,因此可以表示输入样本属于多个互斥离散集合的概率分布。那么为什么不用之前提到的平方误差呢?假设期望输出为1,实际输出为十亿分之一,那么梯度将不会被反向传播来让logistic单元发生变化,因为此时进入了激活函数的饱和区,梯度近似为0。即这样非常大的误差实际上基本不会修改网络中的权重。另外,如果要设计的输出是某个样本属于不同标签(标签间互斥)的概率,那么实际上我们知道输出总和应该是1,这个先验知识应该告知给神经网络。因此,可以修改输出函数来传递这一特征,即使用softmax函数。这个函数可以看作是max函数的软连续(soft continous)版本:记第\(i\)个神经元的输出为\(z_i\)(称为分对数logit),其经过softmax函数转换得到的输出不只依赖于\(z_i\)本身,而是依赖于这一组中所有的\(z\),即 \[ y_i = \frac{e^{z_i}}{\sum_{j \in {\rm group}}e^{z_j}} \] 显然,\(y_i\)满足如下两个性质:
- \(0 < y_i \le 1\)
- \(\sum_i y_i = 1\)
因此\(y_i\)就可以看作是输入属于类别\(i\)的概率值。其对原始输入\(z_i\)的梯度为 \[ \begin{align*} \frac{\partial y_i}{\partial z_i} &= \frac{e^{z_i}\sum_je^{z_j} - e^{z_i}\cdot e^{z_i}}{(\sum_j e^{z_j})^2} \\ &= \frac{e^{z_i}}{\sum_j e^{z_j}} - \left(\frac{e^{z_i}}{\sum_je^{z_j}}\right)^2 \\ &= y_i - y_i^2= y_i(1-y_i) \end{align*} \] 现在的问题是,如果使用softmax函数做输出函数,对应的代价函数应该怎么选择?答案是像往常一样,最合适的代价函数是正确答案的负对数概率,也就是说,要最大化得到正确答案的概率的对数值。因此,如果目标值的某一位为1,其余位为0,则只需要将所有可能答案相加,让错误的答案与0相乘,让正确的答案与1相乘,就能得到正确答案的负对数概率。得到的这个代价函数称为交叉熵代价函数,假设目标值为\(\bf t\),在第\(j\)个维度的分量为\(t_j\),则交叉熵代价函数\(C\)可以写为 \[ C = -\sum_j t_j\log y_j \] 交叉熵代价函数的一个优美性质是当期望目标值为1,输出接近0时,梯度非常大。使用链式求导,有 \[ \frac{\partial C}{\partial z_i} = \sum_j \frac{\partial C}{\partial y_j} \frac{\partial y_j}{\partial z_i} = y_i - t_i \] 尽管\(\partial y_j / \partial z_i\)可能很平,但是\(\partial C/\partial y_j\)会很陡,一定程度上减轻梯度饱和的影响
附:向量化求交叉熵代价函数梯度的过程
(这也是CS224n的一次作业)
假设期望的输出为\(\boldsymbol{y}\),实际输出为\(\boldsymbol{t}\),softmax的输入为\(\boldsymbol{z}\),则有 \[ \begin{align*} \boldsymbol{y} &= {\rm softmax}(\boldsymbol{z}) \\ C(\boldsymbol{t}, \boldsymbol{y}) &= -\sum_i t_i\log(y_i) \end{align*} \] 由于\(\boldsymbol{t}\)是独热编码,不失一般性,假设第\(k\)个分量为1,其余分量均为0,则有 \[ t_i = \begin{cases} 1 & {\rm if\ }i=k \\ 0 & \rm{elsewhere}\end{cases} \] 因此展开交叉熵代价函数为 \[ \begin{align*} -\sum_i t_i\log(y_i) &= -t_k\log(y_k) = -\log(y_k) \\ &= -\log\frac{e^{z_k}}{\sum_ie^{z_i}} = -z_k + \log\sum_ie^{z_i} \end{align*} \] 所以 \[ \begin{align*} \frac{\partial C(\boldsymbol{t}, \boldsymbol{y})}{\partial \boldsymbol{z}} &= \begin{cases} -1 + \frac{e^{t_i}}{\sum_i e^{t_i}} & {\rm if\ }i = k \\ \frac{e^{t_i}}{\sum_i e^{t_i}} & {\rm elsewhere} \end{cases} \\ &= \boldsymbol{y}-\boldsymbol{t} \end{align*} \]
神经概率语言模型
利用前面提取姓名特征的方法,可以得到单词的特征向量表示,得到的向量称为词向量。词向量在语音识别领域非常有用(笔者注:现在词向量基本已经成了NLP各个问题的基石,不再被语音识别所独享):如果背景音比较嘈杂,那么很难单纯从原始的声音输入辨别音素。对于同样的声音信号,可能有多个不同的单词都能与之很好对应。例如,如果背景音嘈杂,就很难分辨beach和speech这两个词。人能做到这一点是无意识的,但是同样的方法不能用在机器上。因此,语音识别的研究人员需要根据给定的上文来判断下一个单词更可能是哪个,即建立一个语言模型
传统的语言模型是使用N元语法,通常N为3。即,采集大量语料,统计所有三元词组出现的频率,然后根据这些频率信息利用相对概率来猜在给定了前两个单词的情况下第三个单词会是什么。例如,假设前面两个词已知是a和b,判断下一个词是c还是d,则有 \[ \frac{p(w_3 = {\rm c} | w_2 = {\rm b}, w_1 = {\rm a})}{p(w_3 = {\rm d} | w_2 = {\rm b}, w_1 = {\rm a})} = \frac{\rm count(abc)}{\rm count(abd)} \] 三元语法的问题是对上文的信息利用有限,它不能利用更多的上文进行推断。其原因一方面在于,使用类似的方法,上文越丰富,需要存储的频率数据越多,可能会压爆内存;另一方面是,词组空间变大会使得大部分词组出现的次数接近于0,因此概率趋近于0。有时,如果三元组不存在或者概率太小,则需要回退到二元语法,考察二元组出现的频率。也就是说,使用这种方法,大部分情况下说“ab后面接c的概率是0”只是因为某个词组出现的频率为0,而这种做法是不正确的
此外,三元语法难以捕获一些更深层的信息。例如,假设看过“the cat got squashed in the yard on Friday”,那么理应可以对“the dog got flattened in the garden on Monday”这样的句子中的词做出不错的预测。但是N元语法做不到这点,因为仅凭统计学上的信息难以得出dog-cat,squashed-flattened,yard-garden,Friday-Monday这样的关系
为了突破N元语法的种种限制,一种解决思路是把单词转化成包含语义和语法特征的向量,然后使用前面若干词的特征来预测后面单词的特征。使用这种特征表示法可以把更大的上文利用起来,例如可以使用前十个词的特征
Bengio等人提出了一种神经网络结构来预测下一个单词,这个结构如图所示
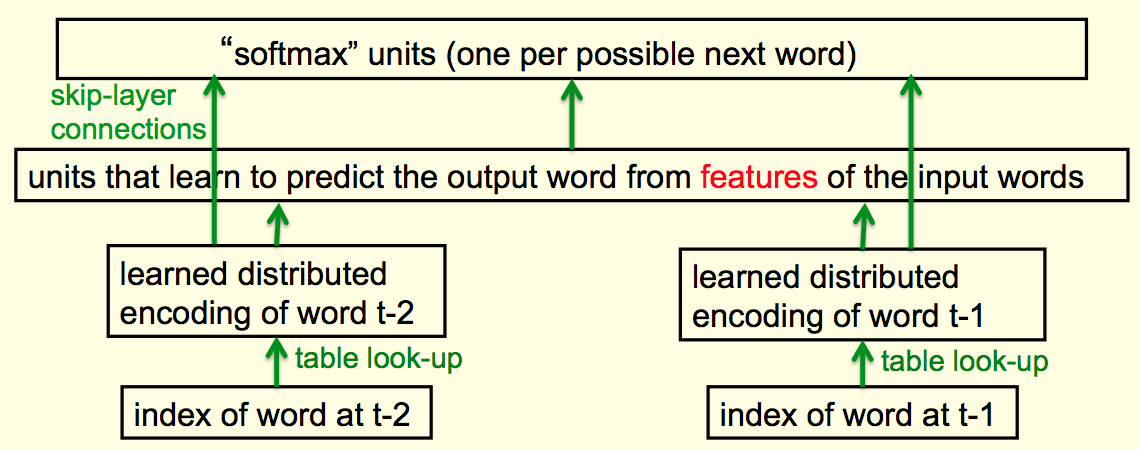
网络的最底层可以看作是单词索引,也可以看作是一组神经元,只是每时每刻都只有一个神经元被激活。这个被激活的神经元会决定接下来这个隐藏层的行为模式,也就是其所对应的单词的分布式表示(即这个单词的词向量)。由于索引和词向量一一对应,因此整个过程等价于查表,但是这个词向量可以通过学习过程来修改
有了词向量,就可以通过另一个隐藏层和softmax层来得出所有单词出现在下一个位置上的概率。不过,更好的做法是是直接用学到的词向量连接到softmax层,因为词向量本身就包含了足够的信息来预测下一个单词
这个结构的问题是最后的输出层很大,需要处理大概十万个单词(因为这种情况下通常一个词的不同形态对应不同单词,例如cat和cats被看做是两个单词),因此整个网络中权重就更多,容易过拟合。如果我们不像Google那样有大量的数据,就需要试着减小隐藏层单元的数量。但是,这样就难以算出这十万个单词的准确概率,会导致大量单词的概率非常小,而这些小概率通常会比较相关。例如,语音识别工具要判断两个罕见词哪个更应该出现,即便两者出现的概率都不大。因此,需要一种方法来处理这样大量的输出
处理神经概率语言模型的大量输出
为了避免在输出层设置十万个输出单元,一种比较有效的方法是使用序列结构。也就是说,前面还是上文单词,但是最后放置要输出单词的一个候选词,这样,神经网络的输出是这个候选词的分对数得分。这种做法的问题是当候选词有多个词的时候需要把神经网络跑好几遍。在得到所有可能候选词的得分以后,可以把这些得分单独送进softmax函数,得到每个单词的概率。使用这个预测概率和目标概率(实际通常是一个某维度为1其余为0的向量)可以计算两者的交叉熵,利用这个误差函数可以反向传播梯度更新权重。如果候选词集合比较小(例如先用N元语法筛一遍),这种做法还是很有效的
另一种做法是使用二叉树,树的叶子节点是所有单词。使用前面单词的上文信息可以得到一个预测向量\(\boldsymbol{v}\),然后将\(\boldsymbol{v}\)与树中的每个内部节点学到的向量\(\boldsymbol{u}_i\)做内积,对得到的内积计算一次logistic函数,则走向右子树的概率为\(\sigma(\boldsymbol{v}^\mathsf{T}\boldsymbol{u}_i)\),走向左子树的概率为\(1-\sigma(\boldsymbol{v}^\mathsf{T}\boldsymbol{u}_i)\)。这样沿着某条确定的路径走下去就可以找到期望的单词。具体做的时候,只需要把上文中单词的词向量加起来就能得到预测向量\(\boldsymbol{v}\)。接下来,对于某个已知的期望单词,要做的就是让从根节点走向这个单词的路径概率尽可能大。例如下图中就要让红色的路径(\(i\rightarrow j\rightarrow m\))的概率尽可能大
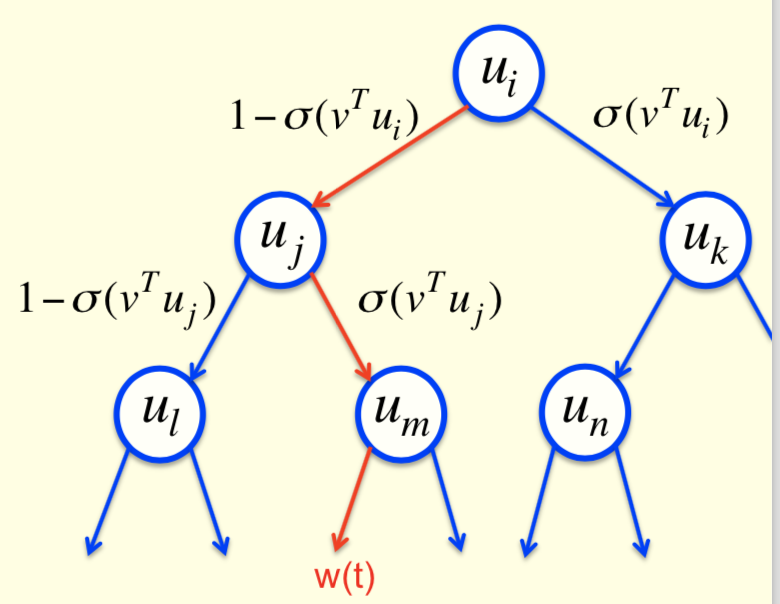
因此,为了让选中正确目标单词的概率最大化,就需要试着最大化选中通向正确单词路径的对数概率和。因此在学习时,只需要关注正确路径上的节点。相比于原来\(O(N)\)的复杂度,这种做法在学习时的复杂度降低到了\(O(\log N)\)。对每个节点,由于知道下一个单词是什么,因此知道正确的路径。而且,通过将预测向量与每个节点的学习向量求内急,可以知道选择每条路径的概率。因此,可以求得误差函数关于\(\boldsymbol{u}_i\)和\(\boldsymbol{v}\)的梯度,所以训练起来会非常快。不过这种做法的问题是测试时仍然很慢,因为此时需要考虑很多单词的概率,所以不能只专注于一条路径
Collobert和Weston提出了一种更简单的学习词向量的方案。他们做的不是预测下一个单词,而是只是学出一些词向量,然后将这些词向量用在一些不同的NLP任务中。此外,他们不只使用上文信息,还是用下文信息,因此实际使用的是一个长度为11的词窗口,其中有5个词出现在上文,5个出现在下文。窗口中间位置他们选择放一个正确的单词(的确出现在这个语境里)或者放一个随机挑选的单词。训练出来的神经网络应该对正确的单词输出高分,对随机的单词输出低分。训练预料均来自于wiki,大概有6亿条数据。得到的词向量使用t-sne降维到二维空间并做出图以后可以展现出令人吃惊的效果,语义上相近的词在空间中也聚集在一起。这意味着上下文信息实际上能够透露很多关于单词意义的信息,事实上,有些人认为这也是人类学习词语意义的主要方式。例如,假如你从未听说过scrommed这个单词,但是看到she scrommed him with the frying pan这句话,应该也能猜出来这是什么意思
(后面具体例子略,毕竟现在词向量已经为人所熟知了:) )
参考文献
Collobert, Ronan, and Jason Weston. "A unified architecture for natural language processing: Deep neural networks with multitask learning." Proceedings of the 25th international conference on Machine learning (ICML). ACM, 2008. (pp. 160-167)
Mnih, Andriy, and Geoffrey E. Hinton. "A scalable hierarchical distributed language model." Advances in neural information processing systems (NIPS). 2009. (pp. 1081-1088)
