本讲原标题有点标题党,只讲了一点关于深度学习的皮毛,还有一部分在讲PCA,不要被误导!
本讲原标题有点标题党,只讲了一点关于深度学习的皮毛,还有一部分在讲PCA,不要被误导!!
本讲原标题有点标题党,只讲了一点关于深度学习的皮毛,还有一部分在讲PCA,不要被误导!!!
深度神经网络
神经网络的核心是一层层的神经元和它们之间的连接关系。一个比较直接的问题,是应该如何设计神经网络?它应该有多少层,每一层各自应该有多少神经元?或者更泛泛地说,应该选择什么样的网络结构?这是神经网络应用时一个非常核心也非常困难的问题。神经网络结构可以粗浅地分成两种:浅层神经网络和深度神经网络,两者区别是前者只有少量的隐藏层,而后者有很多层。浅层神经网络训练起来更有效,关于结构的决定更简单,有足够有力的理论基础。相比而言,深度学习训练起来比较难,也难以决定网络的结构。但是当层数足够多时,网络的能力也会非常强,而且它可以提取出有物理意义的特征
例如,现在要分辨手写的数字是1还是5,那么可以先想办法在笔记里萃取出各个部位的笔画特征,例如中间是竖,底层是不是弯等等。这些特征(笔画)可能通过组合变得更复杂,到最后一步再用来做辨识动作,如下图所示
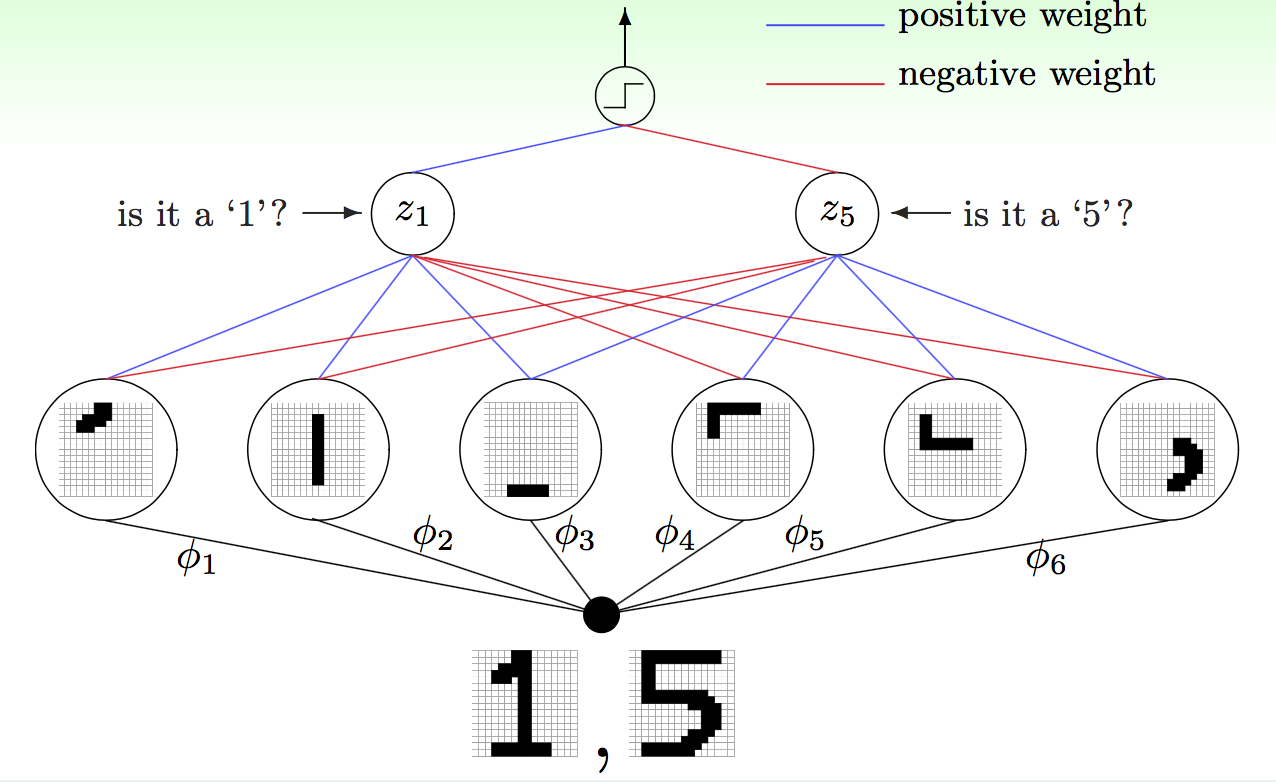
这里实际每一层都可以解读出物理意义。例如要辨识1,可能需要\(\phi_1, \phi_2, \phi_3\),不需要\(\phi_4, \phi_5, \phi_6\)。这样看,第一层其实做的是从像素点提取笔画的功能,第二层则是对第一层做组合,设计不同权重,等等。层数越多,就能表示越多种不同的变化,每层要做的事情也相对来讲变得更加简单。在这种架构下,每一层只需要贡献出一份微薄的力量,做一点微小的工作,就可以使整个网络完成从简单特征到复杂特征的变换。因此,深度学习适用于那些难以从原始特征做学习的任务,例如语音处理
前面提到过深度学习会面临几个难题,目前(2015年)主要采取如下的方式来应对
- 难以决定具体应使用何种网络结构:使用一些领域知识,加入对问题的了解。例如处理图像时使用卷积神经网络(Convolutional NN,CNN),这样让每层神经元都只处理一小块像素
- 模型复杂度很高:如果数据足够大,就不是问题。如果的确想控制模型复杂度,想容忍噪声,就使用一些特有的正则化方法,例如dropout(训练时随机丢弃一部分隐藏层神经元)或者降噪(denoising,后面介绍)
- 难以最优化:谨慎选择初始权重,以避免陷入差的局部最优解(称为预训练)
- 过高的计算复杂度(尤其是在大数据背景下此问题更严重):使用新的硬件和体系结构,例如使用GPU做mini-batch
本讲无法涵盖所有深度学习的技巧,只能介绍一点入门的部分。这里再多说几句,介绍一种比较简单的预训练方法。不像之前提到的神经网络那样上来对所有权重做决定,这里使用了一种分层决定的方法:对第\(\ell = 1,\ldots , L\)层,假设\(w_\ast^{(1)}, \ldots, w_\ast^{(\ell -1)}\)都已经固定,一层一层去对\(\{w_{ij}^{(\ell)}\}\)做预训练。每层权重都预训练好了以后,再使用反向传播来调优所有的\(\{w_{ij}^{(\ell)}\}\)。接下来的问题就是怎么在每一层进行预训练,以及怎么加入正则化来控制模型复杂度
自动编码器
前面讲过,预训练的意义是寻找一个好的初始化权重,那么什么叫“好的”初始化权重呢?这里引发了我们对权重的物理意义的思考。由前面的讲解,可知权重本质上是告知模型如何做特征变换,或者说,怎么把原始数据换一种表示形式(称为经过了一次编码)。做深度学习时,并不知道初始化(预训练得到)的权重在后面会被如何调整。既然如此,不如希望预训练后得到的权重能够(精炼地)保持原始数据的特征:传给后面神经元的数据不是乱七八糟的,而是对相同信息的一种不同表示。例如,对前面的手写数字例子,第一层提取出的笔画特征经过组合,可以还原出原始的数据。那么什么是维持原来数据的特征变换呢?如果使用变换后的数据可以轻易重建原来的数据,就说明原始数据的信息没有什么损失。也就是说,我们希望深度学习预训练时得到的特征变换(初始权重)都是能保持原始信息的
那么如何得到这种能保持原始信息的特征变换呢?一种做法就是仍然使用一个神经网络来解决:把原始的数据通过变换送入到隐藏层神经元以后,这些神经元的输出经过一些变换还能还原成原始的输入(与原始的输入类似)。这个神经网络\(g\)有一个独特的名字,称为自动编码器,它是一个\(d-\tilde{d}-d\)三层的神经网络,从输入层到隐藏层是编码操作,从隐藏层到输出层是解码操作,保证最后输出\(g_i({\bf x}) \approx {\bf x}_i\)(也就是说,此网络是学习逼近一个恒等函数)。其中\(\tilde{d}\)是编码的维度。整个自动编码器的结构如下图所示

其中\(w_{ij}^{(1)}\)称为编码权重,\(w_{ji}^{(2)}\)称为解码权重
那么为什么要设计这么一个复杂的结构,费劲去逼近一个恒等函数(相当于一个什么也不做的函数)?如果真的能得到\(g({\bf x}) \approx {\bf x}\),则它必然依赖了原始数据一些隐藏的特征/结构。如果能通过这个学习过程得到隐藏的特征/结构,那么就可以把这些特征/结构当做特征变换,用在预训练中。这些特征/结构告诉我们如何用一些有效的信息表示原始数据。对于非监督学习问题,自动编码器也有其实际意义。例如如果要做密度估计问题,则对于密度大的区域,编码器能学习得比较好,会更有\(g({\bf x}) \approx {\bf x}\)。那么对应的,如果对于新的数据有\(g({\bf x}_n) \approx {\bf x}_n\),就说明它落在了密度大的区域。如果要做离群点检测,就可以通过\(g({\bf x}_n) \not\approx {\bf x}_n\)来找出离群点。也就是说,学习数据的隐藏特征/结构,也就是在学习什么样的数据是“典型的”数据,自动编码器可以判断数据典型与否
综上所述,自动编码器的目标看似只是学好恒等函数,实际它只是表象。重要意义是看隐含层,看数据有效的表示方式
如前面所述,自动编码器就是一个结构为\(d-\tilde{d}-d\),使用\(\sum_{i=1}^d (g_i({\bf x}) - x_i)^2\)做误差函数的神经网络。它是一种浅层神经网络,因此容易训练。而且,通常\(\tilde{d} < d\),以保证学到的是原始数据的压缩表示。构造的数据集是\(\{({\bf x}_1, {\bf y}_1 = {\bf x}_1), ({\bf x}_2, {\bf y}_2 = {\bf x}_2), \ldots, ({\bf x}_N, {\bf y}_N = {\bf x}_N)\}\)(不看数据集中的标签,因此通常这个学习过程被看做是无监督学习的过程)。有时,还会加入限制条件\(w_{ij}^{(1)} = w_{ji}^{(2)}\)做正则化,不过这样会使最后计算梯度的过程更加复杂
所以,回到上节最后,讲述深度学习如何初始化权重的方法。这个方法里提到说,初始化方法最有效的一招是每一层做一个预训练,这个预训练的过程就是用前一层的输出(对于第一层,是用输入数据)\(\{ {\bf x}_n^{(\ell -1)}\}\)训练一个自动编码器,该自动编码器的隐藏层神经元数\(\tilde{d}\)与深度神经网络中第\(\ell\)层的节点个数\(d^{(\ell)}\)相等
使用不同的体系结构加上不同的正则化,可以得到更精巧的自动编码器,进而得到更好的预训练结果。不过其本质都是相同的
降噪自动编码器
前面讲述了如何在深度学习里做权重的预训练,这一节主要看一看如何加入一些独有的正则化技巧。前面提到过,深度学习里用到的正则化方法包括对结构做出一些限制、加入与权重有关的正则项以及提早结束训练等。但是考虑过拟合的成因,如果数据中噪声太大,也会造成过拟合。因此还可以再独辟蹊径,找到一种方法去降低噪声,这样也可以降低过拟合的风险。最简单的方法是直接做数据清洗,不过一种更疯狂的方法是向数据里加入噪声
在上一节里,自动编码器逼近的是恒等函数,即使得\(g({\bf x}) \approx {\bf x}\)。但是一个足够鲁棒的自动编码器不仅能做到这一点,对于与输入有些微不同的\(\tilde{\bf x}\),还能做到\(g(\tilde{\bf x}) \approx {\bf x}\)。也就是说,送进干净的数据可以产生干净的数据,而送进脏数据也可以出来干净的数据。这意味着足够鲁棒的自动编码器还能起到降噪,清洗数据的功能。因此,训练编码器时,可以故意往训练数据里加入一些人工噪声。即此时输入数据为\(\{(\tilde{\bf x}_1, {\bf y}_1 = {\bf x}_1), (\tilde{\bf x}_1, {\bf y}_2 = {\bf x}_2), \ldots, (\tilde{\bf x}_N, {\bf y}_N = {\bf x}_N)\}\),其中\(\tilde{\bf x}_n = {\bf x}_n + 人工噪声\)。通过这种方法训练出来的自动编码器一般称为降噪自动编码器,在深度学习中通常是使用它,而不是原始的自动编码器。加入人工噪声这种方法告诉了算法我们所需要的性质,得到的模型对噪声容忍度有了很大的增强,因此这种手段也可以看作是一种正则化机制,可以适用到其它模型训练的过程中
主成分分析(PCA)
前面提到的自动编码器实际上是一种非线性模型,但是前面的课程一直都在说模型应该从最简单的,线性的模型试起,为什么这次反其道而行之了?原因是线性编码器是在深度学习预训练权重的背景下提出,而深度学习本身就是一个非线性的问题,因此在这个背景下直接讨论非线性的解决方案更有意义
当然,自动编码器也存在其线性形式,而且线性的自动编码器也有很多适用场合,因此仍然有研究的必要。线性自动编码器类似于前面提到的非线性自动编码器,只不过在对输入\(\bf x\)求出得分以后不需要再做非线性变化\(\tanh\)。这样一来,对\(\bf x\)的第\(k\)个维度,其假设函数形式可以写为 \[ h_k({\bf x}) = \sum_{j=0}^{\tilde{d}}w_{kj}\left(\sum_{i=1}^d w_{ij}x_i\right) \] 注意内层求和项的指标是从1开始计数,因为对常数项逼近一个恒等函数没什么意义。此外,这里加入了前面所提到的正则化手段,即编码器和解码器的权重相等,\(w_{ij}^{(1)} = w_{ji}^{(2)}\),这里统一写成了\(w_{ij}\)。以及,为了避免产生非平凡解,且考虑到实际要得到的是原始数据的压缩表示,还限制编码后数据的维度\(\tilde{d}\)要小于原始维度\(d\)。这样,记所有权重组成的矩阵为\(\rm W\),线性自动编码器假设函数的形式为 \[ h({\bf x}) = {\rm WW}^\mathsf{T}{\bf x} \] 既然假设函数的形式已经被定义好,那么接下来的做法似乎水到渠成:只需要按部就班写出损失函数,就可以让损失函数对\(\rm W\)求偏导,找出最优的\(\rm W\)。损失函数的形式为(由于最后求出来的是一个向量,因此下面公式中用了黑体\(\bf h\)) \[ E_{\rm in}({\bf h})= E_{\rm in}({\rm W}) = \frac{1}{N}\sum_{n=1}^N \left\|{\bf x}_n - {\rm WW}^\mathsf{T}{\bf x}_n\right\|^2,\ \ {\rm W} \in \mathbb{R}^{d\times \tilde{d}} \] 前面讲到的线性问题都可以得到一个解析解,但是这里乍看之下并不容易,因为求和项里实际上是\(w_{ij}\)的四次多项式,求解起来可能要费点周折,需要使用一些线性代数里的工具。由于\(\rm WW^{\mathsf{T}}\)是半正定矩阵,因此可以对它做特征值分解,记为\(\rm WW^\mathsf{T} = V\Gamma V^{\mathsf{T}}\)。这里得到的\(\rm V\)是正交矩阵,即\({\rm VV^\mathsf{T} = V^\mathsf{T}V = I}_d\),而\(\rm \Gamma\)是一个对角矩阵,由特征值组成,对角线上非零元素的数量至多为\(\tilde{d}\)个。因此\({\rm WW^\mathsf{T}}{\bf x}_n = {\rm V\Gamma V}^\mathsf{T}{\bf x}_n\),接下来可通过优化\(\rm V\)和\(\rm \Gamma\)来最小化\(E_{\rm in}\)
在进入下一步之前,先看一下\({\rm WW^\mathsf{T}}{\bf x}_n = {\rm V\Gamma V}^\mathsf{T}{\bf x}_n\)的几何意义。这里原数据左乘一个正交矩阵\({\rm V}^\mathsf{T}{\bf x}_n\)实际上就是对原数据做一个坐标变换,类似于某种旋转或镜像。再左乘\(\rm \Gamma\),由于\(\rm \Gamma\)是对角矩阵且只有至多\(\tilde{d}\)个非零元素,因此这一步是将原数据至少\(d-\tilde{d}\)个维度的分量置为0,然后对其他分量做缩放,得到一个新的坐标。最后再乘\(\rm V\),就是将新的坐标变换到原来的坐标系。因此,类似地,如果对原数据不做任何修改,那么有\({\bf x}_n = {\rm VIV^{\mathsf{T}}}{\bf x}_n\)。原问题就变成了 \[ \min_{\rm V} \min_{\rm \Gamma} \frac{1}{N}\sum_{n=1}^N\left\|{\rm VIV^{\mathsf{T}}}{\bf x}_n - {\rm V\Gamma V^{\mathsf{T}}}{\bf x}_n\right\|^2 \] 首先来看最优的\(\rm \Gamma\)。由于乘以\(\rm V\)和\(\rm V^{\mathsf{T}}\)是旋转和镜像,不改变向量的长度,因此去掉它对最优化问题的解没有影响。即上述问题等价于 \[ \min_{\rm \Gamma}\sum\left\|({\rm I-\Gamma})({\rm some\ vector})\right\|^2 \] 这里\(\rm \Gamma\)是唯一的变量,因此为了让上式小,就要让\(\rm I-\Gamma\)中有尽量多的0。由于\(\rm \Gamma\)是对角矩阵,\(\rm I\)是单位矩阵,那么为了达到效果,就要让\(\rm \Gamma\)的对角线上有尽量多的1。由前面的推导,\(\rm \Gamma\)上最多有\(\tilde{d}\)个1。不失一般性地,最优的\(\rm \Gamma\)可以为 \[ {\rm \Gamma} = \left[\begin{matrix}{\rm I}_{\tilde{d}} & 0 \\ 0 & 0\end{matrix}\right] \] 这样,求解原问题等价于求解如下问题 \[ \min_{\rm V}\sum_{n=1}^N \left\| \left[\begin{matrix}0 & 0 \\ 0 & {\rm I}_{d-\tilde{d}}\end{matrix}\right]{\rm V}^{\mathsf{T}}{\bf x}_n\right\|^2 \] 直观地看,这个问题是在问“对向量\({\rm V}^\mathsf{T}{\bf x}_n\),留下哪几个分量可以使剩下的向量范数最小”。由于原向量是固定的,因此实际上这个问题等价于“对向量\({\rm V}^\mathsf{T}{\bf x}_n\),拿走哪几个分量可以使拿走的向量范数最大”。也就是说,有 \[ \min_{\rm V}\sum_{n=1}^N \left\| \left[\begin{matrix}0 & 0 \\ 0 & {\rm I}_{d-\tilde{d}}\end{matrix}\right]{\rm V}^{\mathsf{T}}{\bf x}_n\right\|^2 \equiv \max_{\rm V}\sum_{n=1}^N \left\| \left[\begin{matrix} {\rm I}_{\tilde{d}} & 0 \\ 0 & 0\end{matrix}\right]{\rm V}^{\mathsf{T}}{\bf x}_n\right\|^2 \] 考虑极端的情况,如果\(\tilde{d} = 1\),此时只与\(\rm V^\mathsf{T}\)的第一个行向量\({\bf v}^\mathsf{T}\)有关。考虑\(\rm V\)是正交矩阵,有\({\bf v}^\mathsf{T}{\bf v} = 1\)。因此可以得到如下最优化问题 \[ \begin{align*} \max_{\bf v}\ \ &\sum_{n=1}^N {\bf v}^\mathsf{T}{\bf x}_n{\bf x}_n^\mathsf{T}{\bf v} \\ {\rm s.t.}\ \ &{\bf v}^\mathsf{T}{\bf v} = 1 \end{align*} \] 使用拉格朗日乘子,可知最优的\(\bf v\)满足 \[ \sum_{n=1}^N {\bf x}_n{\bf x}_n^\mathsf{T} {\bf v} = \lambda {\bf v} \] (推导过程:引入拉格朗日乘子\(\lambda\),可知优化问题转为\(\mathcal{L} = \sum {\bf v}^\mathsf{T}{\bf x}_n{\bf x}_n^\mathsf{T}{\bf v} - \lambda(1-{\bf v}^\mathsf{T}{\bf v})\)。\(\nabla \mathcal{L}_{\bf v} = 2\sum{\bf x}_n{\bf x}_n^\mathsf{T}{\bf v} - 2\lambda{\bf v}\),令\(\nabla \mathcal{L}_{\bf v} = 0\)就可以得到上面这个关系)
而\(\sum_{n=1}^N {\bf x}_n{\bf x}_n^{\mathsf{T}}\)是一个矩阵,如果记为\({\rm X^\mathsf{T}X}\),则根据特征值与特征向量的定义,最优的\(\bf v\)实际上就是\({\rm X^\mathsf{T}X}\)的第一个特征向量。推而广之,最优的\({\rm V} = \{ {\bf v}_j\}_{j=1}^{\tilde{d}}\) 就是\({\rm X^\mathsf{T}X}\)的前\(\tilde{d}\)个特征向量
因此,线性自动编码器就是要把\(\rm X^\mathsf{T}X\)求出来,得到前\(\tilde{d}\)个特征向量的方向,就是应该投影,做特征变换的方向。算法如下
计算\(\rm X^\mathsf{T}X\)的前\(\tilde{d}\)个特征向量\({\bf w}_1, {\bf w}_2, \ldots, {\bf w}_{\tilde{d}}\)
做特征变换\(\boldsymbol{\Phi}({\bf x}) = {\rm W}({\bf x})\)
由上面的推导,可知线性编码器保证输入在投影后的空间里范数总和最大。如果换一个说法,说输入在投影后的空间里方差(变化量)总和最大,那么就是统计学里主成分分析 (PCA) 的做法。PCA算法与线性自动编码器算法大同小异,不过由于其关注的是变化量总和,而变化量实际上是数据相对于平均数的差的平方,因此需要先把数据做一个相对于平均值的变换。PCA算法总体过程如下
令\(\bar{\bf x} = \frac{1}{N}\sum_{n=1}^N {\bf x}_n\),令\({\bf x}_n \leftarrow {\bf x}_n - \bar{\bf x}\)
计算\(\rm X^\mathsf{T}X\)的前\(\tilde{d}\)个特征向量\({\bf w}_1, {\bf w}_2, \ldots, {\bf w}_{\tilde{d}}\)
做特征变换\(\boldsymbol{\Phi}({\bf x}) = {\rm W}({\bf x -\bar{x}})\)
自动线性编码器和PCA都是非常好用的线性维度缩减的工具,可以用来处理数据。不过实践中PCA更常用一些
