AdaBoost决策树
在介绍AdaBoost决策树之前,先回顾一下之前讲过的随机森林。随机森林的核心是,将一些决策树(内层)使用bagging的方法(外层)聚合起来。如果把决策树和AdaBoost算法结合起来,那么就得到了AdaBoost决策树。但是有一点需要注意:AdaBoost算法里要求基算法在训练时能够接受样本的权重,但是之前CART算法不能根据各个样本的权重做调整,因此现在最关键的问题是要对决策树算法作出修改,使其可以接受样本的权重,在每个\(t\)得到不一样的\(g_t\) ,即要实现一个加权的决策树算法\({\rm DTree}(\mathcal{D}, {\bf u}^{(t)})\)
加权算法的核心是,其需要根据权重最佳化根据权重加权过的\(E_{\rm in}\)。因此相对应的有两种处理办法
- 将原有的基算法看作是白盒,查找其在何处修改\(E_{\rm in}\),然后在该处加上对权重的处理逻辑。例如SVM中,就是对应hinge loss的部分。但是决策树算法实现里有很多启发式算法,如果挨个分析哪部分跟\(E_{\rm in}\)有关,就比较麻烦
- 将原有的基算法看作是黑盒,将送入算法的数据做变化。回想之前对bootstrapping的描述,其实质上也隐含了“权重”的概念:权重是3的数据,其实就是该数据复制3份;权重是7的数据,其实就是该数据复制7份。那么,推而广之,对送入算法的数据的变化方法就是根据数据的权重做采样。这样,就可以得到一组大小为\(N'\)的新数据集\(\tilde{\mathcal{D}}_t\),其中每种数据的比例正比于\(\bf u\),也就能体现权重的影响
因此,AdaBoost决策树的核心算法就是,将原始数据集\(\mathcal{D}\)按照\({\bf u}^{(t)}\)做抽样,然后使用得到的新数据集\(\tilde{\mathcal{D}}_t\)按照原有的决策树算法训练。不过这里还有一个矛盾:AdaBoost通常需要一些比较弱的基分类器,而原有的决策树算法初衷是要树完全增长。回想原来AdaBoost里每个基分类器的权重(票数)\(\alpha_t\)是由加权错误率\(\epsilon_t\)决定,即\(\alpha_t = \ln \blacklozenge_t = \ln \sqrt{(1-\epsilon_t)/\epsilon_t}\)。如果决策树\(g_t\)在所有\({\bf x}_n\)上自由生长,且训练数据两两不等,那么就会有\(E_{\rm in}(g_t) = 0\),进而\(E_{\rm in}^{\bf u}(g_t) = \epsilon_t = 0\),即\(\alpha_t = \infty\),这棵树成了一个独裁者!
鉴于上面的情势,考虑AdaBoost的核心思想,为了避免上述状况的发生,还是需要基分类器都足够弱。让基分类器(这里是决策树)足够弱的方法有两种:
- 对决策树进行剪枝,参见前面讲过的剪枝方法。或者一种最简单有效的方法是限制树的高度
- 不送入全部数据,使用前面提到的采样方法。采样概率\(\propto {\bf u}^{(t)}\)
综合以上讨论,可以得到:AdaBoost决策树 = AdaBoost + 采样概率\(\propto {\bf u}^{(t)}\) + 剪枝过的决策树\({\rm DTree}(\tilde{\mathcal{D}}_t)\)
对树做剪枝的极端情况是,树的高度\(\le 1\)。考虑之前讲过的决策树(C&RT算法),树高为1的数只有一个分枝。回顾决策树的分枝条件定义,其要做的是让左右子树各自的不纯度两者加起来的值最小。如果不纯度的定义为二元分类误差,那么实际上此时决策树退化成了一个决策树桩。即前面提到的AdaBoost决策树桩是AdaBoost决策树的一种特殊情况
最优化角度看AdaBoost
之前讲解AdaBoost时,曾经提出过样本权重的更新法则 \[ u_n^{(t+1)} = \begin{cases}u_n^{(t)} \cdot \blacklozenge_t & {\rm if\ incorrect} \\ u_n^{(t)} / \blacklozenge_t & {\rm if \ correct}\end{cases} \] 这个式子可以做进一步化简:考虑之前提到的,如果\(y_n \in \{-1, +1\}\),那么当分类结果正确时,有\(y_ng_t({\bf x}_n) = 1\),否则\(y_ng_t({\bf x}_n) = -1\)。因此上式可以简写为递推式 \[ u_n^{(t+1)} = u_n^{(t)} \cdot \blacklozenge_t^{-y_ng_t({\bf x}_n)} \] 带入\(\blacklozenge_t = e^{\alpha_t}\),可以得到 \[ u_n^{(t+1)} = u_n^{(t)} \cdot \exp(-y_n\alpha_tg_t({\bf x}_n)) \] 将这个递推式展开,有 \[ u_n^{(T+1)} = u_n^{(1)} \cdot \prod_{t=1}^T\exp(-y_n\alpha_tg_t({\bf x}_n)) = \frac{1}{N} \cdot \exp\left(-y_n\sum_{t=1}^T\alpha_tg_t({\bf x}_n)\right) \] 注意最后指数里有一部分可以对应于AdaBoost的总假设函数\(G({\bf x})\) :\(G({\bf x}) = {\rm sign}\left( \sum_{t=1}^T \alpha_tg_t({\bf x})\right)\)。可以将\(\sum_{t=1}^T \alpha_t g_t({\bf x})\)记为\(\{g_t\}\)在\(\bf x\)上的投票得分(voting score)
前面还说过,AdaBoost实际上是一个线性混合的过程:将所有基假设函数看作是对原始数据的一个变换,然后在转换后的空间里学习出一个线性模型,这个线性模型就说明了每个\(g_t\)会占几票。如果将基假设函数的变换过程\(g_t({\bf x}_n)\)写为\(\phi_i({\bf x}_n)\),将每个\(g_t\)的票数写为权重的样子\(w_i\),那么投票得分就可以改写为\(\sum_{i=1}^T w_i\phi_i({\bf x}_n)\)。回顾之前提到的SVM间隔的定义,\({\rm margin} = \frac{y_n \cdot ({\bf w}^\mathsf{T}\phi({\bf x}_n) + b)}{\|{\bf w}\|}\),如果忽略掉这个式子中的常数项\(b\),正则项\(1/\|{\bf w}\|\)和用来判断点是落在分离超平面正确一侧还是错误一侧的\(y_n\),其核心部分\({\bf w}^\mathsf{T}\phi({\bf x}_n)\)其实传递的是点到超平面距离的概念。因此,\(y_n \cdot {\rm voting\ score}\)实际上就是带符号的且没有做过正则化的间隔,我们也希望这个间隔是一个比较大的正数。既然如此,那么\(\exp(-y_n({\rm voting\ score}))\)就应该越小越好,\(u_n^{(T+1)}\)也应该越小越好。实际上,AdaBoost就是在减小\(\sum_{n=1}^Nu_n^{(t)}\),其本质也是要让分离超平面离数据点的间隔变大。也就是说,它要减小的是 \[ \sum_{n=1}^N u_n^{(T+1)} = \frac{1}{N}\sum_{n=1}^N\exp\left(-y_n\sum_{t=1}^T\alpha_tg_t({\bf x}_n)\right) \] 再次搬出之前提到过很多次的线性得分\(s = \sum_{t=1}^T \alpha_t g_t({\bf x}_n)\),以及之前提到的0/1误差函数\({\rm err_{0/1}}(s, y) = [\![ys \le 0]\!]\)。如果将上面的这个式子看作是AdaBoost某种意义上要减小的误差函数,记为\(\widehat{\rm err}_{\rm ADA}\),那么有\({\rm \widehat{err}_{ADA}} = \exp(-ys)\)(称为指数损失函数)也是\(\rm err_{0/1}\)的上界。因此可以说,AdaBoost也是在减小0/1误差函数的凸上限,进而达到解好分类问题的目的
接下来,要证明AdaBoost算法的确可以减小\(\rm \widehat{err}_{ADA}\)。这个证明过程类似于之前提到的梯度下降法(GD),只不过GD是要找到一个向量\(\bf v\)作为下降方向,而AdaBoost是要找到一个基函数\(g_t\)作为下降方向。即在第\(t\)步迭代,为了寻找最优的\(g_t\),就是要求解 \[ \min_h \widehat{E}_{\rm ADA} = \frac{1}{N}\sum_{n=1}^N\exp\left(-y_n\left(\sum_{\tau = 1}^{t-1}\alpha_\tau g_\tau ({\bf x}_n) + \eta h({\bf x}_n)\right)\right) \] 将上式展开,代入\(u_n^{(t)} = \frac{1}{N}\cdot \exp(-y_n \sum_{t=1}^T\alpha_t g_t({\bf x}_n))\),可知 \[ \begin{align*} \min_h \widehat{E}_{\rm ADA} &= \frac{1}{N}\sum_{n=1}^N\exp\left(-y_n\left(\sum_{\tau = 1}^{t-1}\alpha_\tau g_\tau ({\bf x}_n) + \eta h({\bf x}_n)\right)\right) \\ &= \frac{1}{N}\sum_{n=1}^N\exp\left(-y_n\sum_{\tau = 1}^{t-1}\alpha_\tau g_\tau ({\bf x}_n) \right)\cdot\exp(-y_n\eta h({\bf x}_n)) \\ &= \sum_{n=1}^N u_n^{(t)}\exp(-y_n\eta h({\bf x}_n)) \end{align*} \] 将上式在零点附近做泰勒展开,可得 \[ \begin{align*} \min_h \widehat{E}_{\rm ADA} &= \sum_{n=1}^N u_n^{(t)}\exp(-y_n\eta h({\bf x}_n)) \\ &\approx \sum_{n=1}^Nu_n^{(t)}(1-y_n\eta h({\bf x}_n)) \\ &= \sum_{n=1}^N u_n^{(t)} - \eta\sum_{n=1}^N u_n^{(t)}y_nh({\bf x}_n) \end{align*} \] 这就很像之前GD \(\min_{\|v\|=1} E_{\rm in}({\bf w}_t + \eta {\bf v}) \approx E_{\rm in}({\bf w}_t) + \eta {\bf v}^\mathsf{T}\nabla E_{\rm in}({\bf w}_t)\)的形式了!同理,这里\(\sum_{n=1}^N u_n^{(t)}\)是常数项,因此最好的\(h\)会最小化\(\sum_{n=1}^N u_n^{(t)}(-y_nh({\bf x}_n))\)。
由于这里考虑的是二元分类问题,因此\(y_n \in \{-1, +1\}, h({\bf x}_n) \in \{-1, +1\}\)。利用这个性质,展开要最小化的式子,有 \[ \begin{align*} \sum_{n=1}^N u_n^{(t)}(-y_nh({\bf x}_n)) &= \sum_{n=1}^N u_n^{(t)} \begin{cases} - 1 & {\rm if\ }y_n = h({\bf x}_n) \\ +1 & {\rm if\ }y_n \not= h({\bf x}_n)\end{cases} \\ &= - \sum_{n=1}^N u_n^{(t)} + \sum_{n=1}^N u_n^{(t)} \begin{cases} 0 & {\rm if\ }y_n = h({\bf x}_n) \\ 2 & {\rm if\ }y_n \not= h({\bf x}_n)\end{cases} \\ &= -\sum_{n=1}^N u_n^{(t)} + 2\sum_{n=1}^N u_n^{(t)} [\![y_n \not= h({\bf x}_n)]\!] \\ &= -\sum_{n=1}^N u_n^{(t)} + 2E_{\rm in}^{ {\bf u}^{(t)}}(h) \cdot N \end{align*} \] 也就是说,要最小化\(\sum_{n=1}^N u_n^{(t)}(-y_nh({\bf x}_n))\),实质上就是要最小化\(E_{\rm in}^{ {\bf u}^{(t)}}(h)\),而这正是AdaBoost的算法\(\mathcal{A}\)做的事!即\(\mathcal{A}\)找到了一个好的梯度下降的函数方向\(g_t = h\)
根据上面的推导,AdaBoost通过近似最小化\(\widehat{E}_{\rm ADA} = \sum_{n=1}^N u_n^{(t)}\exp(-y_n\eta h({\bf x}_n))\)来找到一个最优的函数\(g_t = h\)。那么在找到\(g_t\)以后,能不能不满足于像原始GD那样每次只移动固定的一小步\(\eta\),而是通过最小化\(\widehat{E}_{\rm ADA} = \sum_{n=1}^N u_n^{(t)}\exp(-y_n\eta g_t({\bf x}_n))\),找一个最优的\(\eta_t\),让这一步迈得大一点?观察求和项里的情况:如果分类正确,即\(y_n = g_t({\bf x}_n)\),则要求和的那一项变为\(u_n^{(t)}\exp(-\eta)\);如果分类错误,就会有\(y_n \not= g_t({\bf x}_n)\),要求和的那一项变为\(u_n^{(t)} \exp(+\eta)\)。因此对求和项分拆并代入\(\epsilon_t\)的定义,有 \[ \begin{align*} \sum_{n=1}^N u_n^{(t)}\exp(-y_n\eta g_t({\bf x}_n)) &= \sum_{n=1}^N \left(u_n^{(t)}[\![y_n = g_t({\bf x}_n)]\!]\exp(-\eta) + u_n^{(t)}[\![y_n = g_t({\bf x}_n)]\!]\exp(+\eta) \right) \\ &= \exp(-\eta)\cdot \sum_{n=1}^N u_n^{(t)}\cdot \frac{\sum_{n=1}^N u_n^{(t)}[\![y_n = g_t({\bf x}_n)]\!]}{\sum_{n=1}^N u_n^{(t)}} + \exp(+\eta)\cdot \sum_{n=1}^N u_n^{(t)}\cdot \frac{\sum_{n=1}^N u_n^{(t)}[\![y_n \not= g_t({\bf x}_n)]\!]}{\sum_{n=1}^N u_n^{(t)}} \\ &= \exp(-\eta) \cdot \sum_{n=1}^N u_n^{(t)}\cdot(1-\epsilon_t) + \exp(+\eta)\cdot \sum_{n=1}^N u_n^{(t)}\cdot\epsilon_t \\ &= \sum_{n=1}^N u_n^{(t)}\cdot \left((1-\epsilon_t)\exp(-\eta) + \epsilon_t\exp(+\eta)\right) \end{align*} \] 求解\(\frac{\partial \widehat{E}_{\rm ADA}}{\partial \eta} = 0\)可以得到最优的\(\eta_t\),而 \[ \begin{align*} &\frac{\partial \widehat{E}_{\rm ADA}}{\partial \eta} = 0 \\ \Leftrightarrow & \sum_{n=1}^N u_n^{(t)}\cdot \left(-(1-\epsilon_t)\exp(-\eta) + \epsilon_t\exp(+\eta)\right) = 0 \\ \Leftrightarrow & -(1-\epsilon_t) + \epsilon_t\exp(+2\eta) = 0 \\ \Leftrightarrow & \exp(+2\eta) = \frac{1-\epsilon_t}{\epsilon_t} \\ \Leftrightarrow & \eta = \ln\sqrt{ \frac{1-\epsilon_t}{\epsilon_t}} = \alpha_t \end{align*} \] 因此,其实\(\alpha_t\)是跨度最大的\(\eta_t\)
综上所述,AdaBoost是沿着近似函数梯度(方向是函数而不是向量),向最优方向做了最大程度的下降
梯度提升
对上一节所讲的内容做一个总结,就是AdaBoost每一步都是在最小化指数误差:每一步找到一个\(h\)作为\(g_t\),然后决定要走多远,这个跨度就是\(\alpha_t\)
既然AdaBoost实际上每一步都是在最小化某个误差函数,那么可否对其进行扩展,让其每一步优化的误差函数可以是之前讲过的那些误差函数?答案是肯定的,扩展以后得到的算法称为梯度提升算法(Gradient Boosting),形式为 \[ \min_\eta\min_h \frac{1}{N}\sum_{n=1}^N{\rm err}\left(\sum_{\tau=1}^{t-1} \alpha_\tau g_\tau ({\bf x}_n) + \eta h({\bf x}_n), y_n\right) \] 在这个框架下,就可以使用不同的\(h\)来做Boosting,解决不同的问题
例如,如果要使用Boosting方法求解回归问题,将\(\sum_{\tau = 1}^{t-1}\alpha_\tau g_\tau({\bf x}_n)\)写成\(s_n\),那么误差函数就应该是平方误差,\({\rm err}(s, y) = (s - y)^2\)。对上式内层求最小\(h\)的问题,在零点做泰勒展开,有 \[ \begin{align*} \min_h \frac{1}{N}\sum_{n=1}^N {\rm err}(s_n + \eta h({\bf x}_n), y_n) &\approx \min_h \frac{1}{N} \sum_{n=1}^N {\rm err}(s_n, y_n) + \frac{1}{N}\sum_{n=1}^N \eta h({\bf x}_n)\frac{\partial {\rm err}(s, y_n)}{\partial s}{\huge|}_{s=s_n} \\ &= \min_h {\rm constants} + \frac{\eta}{N}\sum_{n=1}^N h({\bf x}_n)\cdot2(s_n - y_n) \end{align*} \] 由于是一个最小化问题,因此要让\(h\)越小越好。如果\(s_n - y_n\)为正,那么\(h\)就应该为负;否则\(h\)就应该为正。但是这里没有限制,因此此时有\(h({\bf x}_n) = -\infty \cdot (s_n - y_n)\)。由于要做的只是寻找一个方向,因此这里可以(也应该)对\(h\)的大小做一个限制,\(h\)的大小由\(\eta\)来解决。直观的做法是在求解时对\(h\)的大小做一个限制,例如\(\|h\|=1\),但是有限制的最优化问题求解起来比较麻烦。另一种方法,是借鉴拉格朗日乘子和\(\ell_2\)正则化的思想,将\(h\)的大小作为惩罚项放进要求解的问题中,有 \[ \begin{align*} \min_h &&&{\rm constants} + \frac{\eta}{N}\sum_{n=1}^N(2h({\bf x}_n)(s_n - y_n) + (h({\bf x}_n))^2) \\ &=&&{\rm constants} + \frac{\eta}{N}\sum_{n=1}^N\left({\rm constant} + (h({\bf x}_n) - (y_n -s_n))^2\right) \end{align*} \] 如果将上式所有常数项都去掉(其存在与否不影响结果),那么其实就是要找\(\min_h \sum_{n=1}^N (h({\bf x}_n) - (y_n - s_n))^2\),而这个问题实际上还是一个回归问题,只不过此时目标值从\(y_n\)变成了残差\(y_n - s_n\)。因此用来做回归的梯度提升就是通过对残差做回归,来找到最优的\(g_t = h\)
在有了最优的\(h\)以后,接下来就是要求解最优的\(\eta\)。这个优化问题可以写为 \[ \begin{align*} &\min_\eta \frac{1}{N}\sum_{n=1}^N (s_n + \eta g_t({\bf x}_n) - y_n)^2 \\ = &\min_\eta \frac{1}{N}\sum_{n=1}^N ((y_n - s_n) - \eta g_t({\bf x}_n))^2 \end{align*} \] 其实质是一个单变量的线性回归问题,输入是经过\(g_t\)变换过的原始输入,输出是残差项
将上述内容组合在一起,就可以得到梯度提升决策树算法(GBDT)
\(s_1 = s_2 = \ldots = s_N = 0\)
对\(t=1,2,\ldots, T\)
- 使用\(\mathcal{A}(\{({\bf x}_n, y_n-s_n)\})\)获得\(g_t\),其中\(\mathcal{A}\)是一个最小化平方误差的回归算法,通常是被剪枝过的C&RT决策树
- 计算\(\alpha_t = {\rm OneVarLinearReg}(\{(g_t({\bf x}_n), y_n-s_n)\})\)
- 更新\(s_n \leftarrow s_n + \alpha_t g_t({\bf x}_n)\)
返回\(G({\bf x}) = \sum_{t=1}^T \alpha_t g_t({\bf x})\)
GBDT是AdaBoost-决策树用来求解回归问题的“表亲”,在实践中非常常用
(笔者注:GBDT的两个很有名的实现XGBoost和LightGBM也可以用来求解分类问题,sklearn也有GBDTClassifier)
聚合模型方法综述
至此,所有聚合模型已介绍完毕,这里对它们做一回顾
模型的混合法,是在得到各个不同的\(g_t\)以后做聚合,分为一下三种混合方式
- 均匀混合:每个\(g_t\)票数相同,追求模型的复杂性
- 非均匀混合:实际上就是对输入通过\(g_t\)做一个变换,然后训练一个线性模型。其追求的是模型的复杂性,但是需要小心使用,防止过拟合
- 条件混合:与非均匀混合类似,只不过最后训练的是非线性模型。这种方法通常又称为模型的堆叠法(stacking)。其追求的也是模型的复杂性
模型的学习法,是一边学习\(g_t\)一边做聚合。关系可见下图
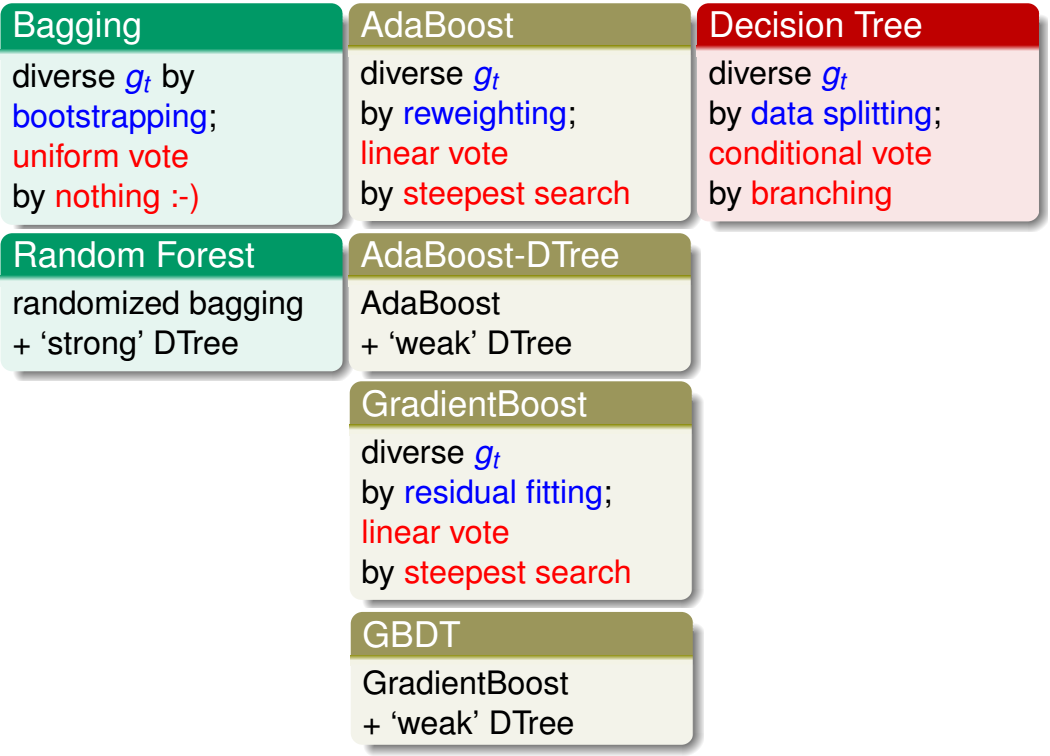
其中随机森林、AdaBoost-DTree和GBDT都是很常用的模型
模型聚合有时可以起到特征变换的作用,使得最后得到的\(G({\bf x})\)很强,避免了欠拟合的问题;有时可以起到正则化的作用,使最后得到的\(G({\bf x})\)不偏不倚,避免了过拟合的问题。总之,适当的模型聚合(有时又称组合ensemble),可以得到更好的效果
