决策树假设
模型聚合总体来讲有两种面向。一种是模型混合法,即在已经知道有哪些基分类器\(g_t\)以后做聚合,返回聚合得到的模型\(G\);另一种是模型学习法,即事前不知道有哪些基分类器,一边求\(g_t\)一边做聚合。聚合这些模型时,总体来讲又有三种方式:将每个\(g_t\)按照等权重聚合、按照重要性分配不同权重聚合,以及按照条件做聚合。决策树就是一种传统的实现条件聚合的学习模型,模仿了人类做决策的过程
之前讲的所有方法可以按照如上的划分方式做出下表
| 聚合形式 | 混合 | 学习 |
|---|---|---|
| 均匀 | 投票法/求均值法 | Bagging |
| 非均匀 | 线性组合 | AdaBoost |
| 条件 | 堆叠法 | 决策树 |
下图给出了一个使用决策树决定是否学习MOOC课程的例子
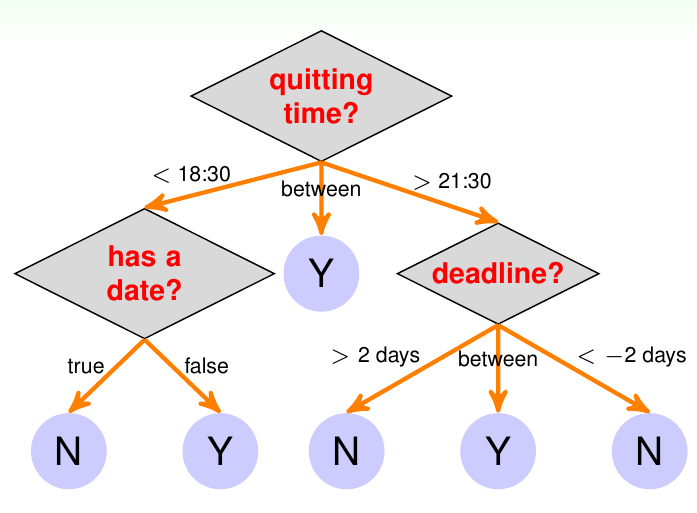
从图中可知,从决策树的树根出发,其到任意一个叶子节点的路径都是一个完整的决策过程
接下来,考虑如何表示决策树的假设模型。如前所述,决策树是一个条件模型,因此可以套用第23讲的内容,将其最基本的形式写出,为 \[ G({\bf x}) = \sum_{t=1}^T q_t({\bf x})\cdot g_t({\bf x}) \] 这里的基假设\(g_t\)其实就是路径\(t\)中最后一个节点(叶子节点)的内容,通常是一个常数。条件\(q_t({\bf x})\)是上图中橘色的箭头,可以写为\([\![{\rm is\ }{\bf x}{\rm \ on\ path\ }t]\!]\),即判断输入是否在某条路径\(t\)上。通常决策的过程(即路径\(t\)上)会有很多简单的决定(在上图中以菱形的内部节点表示)。可以看出,做决定的瞬间并不复杂(即内部节点和叶子节点的操作不复杂),决策树的复杂性是埋藏在条件的抉择中
前面对决策树做出的解释是站在了“决策路径”的角度。从这个角度观察,决策树的假设函数可以写为 \[ G({\bf x}) = \sum_{t=1}^T [\![{\bf x}{\rm\ on\ path\ }t]\!] \cdot {\rm leaf}_t({\bf x}) \] 由于树结构天然的递归性,也可以站在递归的角度对描述决策树。此时,决策树由根节点、分枝条件和子决策树构成。此时决策树的假设函数为 \[ G({\bf x}) = \sum_{c=1}^C [\![b({\bf x})= c]\!] \cdot G_c({\bf x}) \] 这里,\(C\)是由该根节点分出的子树个数,也是该节点的分枝条件数。\(G({\bf x})\)是整棵树对应的假设函数,\(b({\bf x})\)是分枝条件,\(G_c({\bf x})\)是第\(c\)个分枝对应的子树
决策树直观描述了一个做决策的过程,而且跟人的思维方式类似。由于模型的这种可解释性,它被广泛应用在商业和医疗领域的数据分析中。决策树本身算法的实现也不是很难。效率方面,决策树在训练和测试时都非常有效率,因此总体来看决策树是一个很重要的模型。但是决策树没有太多理论解释,其中的原理基本都是来自直觉。决策树的核心算法是一些启发式算法,可能会让初学者感到迷惑,而且没有一个非常有代表性的算法
决策树算法
从上面递归角度定义的决策树的假设函数,可以写出一个基本的决策树算法。记输入数据为\(\mathcal{D} = \{({\bf x}_n, y_n)\}_{n=1}^N\),函数\({\rm DecisionTree}(\mathcal{D})\)的基本思想为:如果其发现满足终止条件,则返回基假设函数\(g_t({\bf x})\),否则递归做如下四步
- 学习分枝条件\(b({\bf x})\)
- 将数据集\(\mathcal{D}\)分为\(C\)个部分,\(\mathcal{D}_c = \{({\bf x}_n, y_n):b({\bf x}_n)=c\}\)
- 对每个分枝条件构建子树\(G_c \leftarrow {\rm DecisionTree}(\mathcal{D}_c)\)
- 返回\(G({\bf x}) = \sum_{c=1}^C [\![b({\bf x})= c]\!] \cdot G_c({\bf x})\)
有上述伪代码可知,具体涉及决策树算法时,需要注意考虑的有四个关键点,包括
- 每一步的分枝数
- 分枝条件
- 终止条件
- 基假设函数
这里要讲的决策树算法是C&RT算法(Classification & Regression Tree,从后文看,其更广为人知的名字应该写作CART算法)。在该算法中,有两点的实现非常简单
- 决策树在每一步都分裂成两棵子树,即\(C=2\)(决策树是一棵二叉树)
- 基假设函数\(g_t({\bf x})\)是一个使\(E_{\rm in}\)最优的常数
- 对分类问题(使用0/1误差函数),返回\(\{y_n\}\)的多数值
- 对回归问题(使用平方误差函数),返回\(\{y_n\}\)的平均值
C&RT在分裂内部节点时使用的是决策树桩算法:选择一个特征,在该特征上选择一个最优分割点切下去,一半判定为正例,另一半判定为负例。那么如何决定怎么切最好呢?算法使用了一种叫做“纯度”的指标来判别。由于C&RT最后每个叶子节点(也就是每个\(g_t\))返回的都是一个常数,显然当这个节点包含的所有数据其\(y_n\)基本相同时(也就是纯度越高时),常数假设函数的效果最好。因此分枝条件的形式为 \[ b({\bf x}) = \mathop{\arg \min}_{ {\rm decision\ stumps\ }h({\bf x})} \sum_{c=1}^2 |\mathcal{D}_c{\rm\ with\ }h|\cdot {\rm impurity}(\mathcal{D}_c{\rm\ with\ }h) \] 上式的意义可以解释为,对所有的决策树桩(每个决策树桩实际对应了一个特征),判断使用该决策树桩将数据集分成两块以后,各个子数据集不纯度的加权总和。不纯度最低的(也就是纯度最高的)决策树桩用来真正做分裂。这里函数\(\rm impurity\)函数用来判定某个数据集的不纯度,后面会定义。不纯度的权重为该数据集的大小
接下来来看算法核心的部分,即数据集的纯度如何定义。由于纯度的作用是为了返回最后最优的那个常数,因此最后返回的常数好还是不好从某种角度就决定了纯度高还是不高。同样的道理,不纯度的也可以由这个常数的\(E_{\rm in}\)来衡量。对于回归问题,不纯度的定义类似于平方误差 \[ {\rm inpurity}(\mathcal{D}) = \frac{1}{N}\sum_{n=1}^N (y_n - \bar{y})^2 \] 其中\(\bar{y}\)是\(\{y_n\}\)的平均值
对于分类问题,做法类似,也可以定义为 \[ {\rm inpurity}(\mathcal{D}) = \frac{1}{N}\sum_{n=1}^N[\![y_n \not= y^\ast]\!] \] 其中\(y^\ast\)是\(\{y_n\}\)的多数值。不过对于分类问题,可以进一步分析:如果使用分类误差,要做的其实是在所有\([\![y_n = k]\!]\)的选择里面,找到最多人资瓷的那个\(K\)。也就是说,分类误差可以写为 \[ 1 - \max_{1\le k \le K} \frac{\sum_{n=1}^N[\![y_n=k]\!]}{N} \] 这个值只有在\(k=y^\ast\)时才能取得最优。进一步地,如果考虑进所有\(k\),可以得到一个新的衡量不纯度的函数,为 \[ 1-\sum_{k=1}^K \left(\frac{\sum_{n=1}^N [\![y_n = k]\!]}{N}\right)^2 \] 该值又称为Gini指数。实际上,在做决策树算法时,如果要解决分类问题,通常用Gini判定不纯度;如果要解决回归问题,通常用回归误差来判定不纯度
最后,考察算法何时终止。事实上,算法在以下两种条件下都会停止
- 所有\(y_n\)都一样,则这个子数据集已经达到了至纯的境地,\(g_t({\bf x}) = y_n\)
- 所有\({\bf x}_n\)都一样,则不会学出决策树桩
使用这种终止条件得到的C&RT决策树,称为一棵完全长成的C&RT决策树
C&RT启发式算法
将上述对四个关键点的设计代回到决策树的基础算法框架中,就能得到一个可用的完整算法。但是这个算法还有一个问题:如果所有\({\bf x}_n\)两两不同,这个算法的\(E_{\rm in}\)必然是0。这意味着这个算法的VC维非常大,很容易有过拟合的危险。尤其是随着分枝的深入,越接近叶子节点时,决策树子树处理的数据实际上越少,这就更增大了过拟合发生的可能性,因此需要向这个算法加入一些正则项
决策树算法中一个很自然的正则项是对树的叶子节点数做一个限制,即\(\Omega(G) = {\rm NumberOfLeaves}(G)\)。这样,带有正则项的决策树要优化的目标函数变为 \[ \mathop{\arg \min}_{ {\rm all\ possible\ }G}E_{\rm in}(G) + \lambda \Omega(G) \] 这样得到的树称作修剪过的决策树
但是注意目标函数里是考虑所有可能的\(G\),这个搜索空间在实际实现时有一些困难,因此需要做一些修改,即实际的搜索空间是
- 完全生长的树\(G^{(0)}\)
- \(G^{(i)} = \mathop{\arg \min}_G E_{\rm in}(G)\),其中\(G\)是从\(G^{(i-1)}\)中拿走一片叶子得到的树(实际上,是将其与其兄弟节点合并得到的树)
此时实际的搜索空间大小就是\(G^{(0)}\)中叶子节点的数目。正则项系数\(\lambda\)仍然是由验证得到
决策树还有一些其他特点。之前考虑的特征基本都是数值特征,分枝时候使用的是决策树桩 \[ b({\bf x}) = [\![x_i \le \theta]\!] + 1,\ \ \theta\in \mathbb{R} \] 但是真正在工作中,可能会遇到大量离散的类别特征,例如性别={男, 女}。对于这种特征,线性模型通常不能直接处理,而决策树不会受到影响,只需要修改一下分枝时用到的模型即可。一般来讲,对类别特征使用的切割方式是使用决策子集 \[ b({\bf x}) = [\![x_i \in S]\!] + 1,\ \ S \subset\{1,2,\ldots, K\} \] (补充一点课堂里没有提到的。对于类别特征,在使用线性模型做处理时,通常的方法是对特征进行独热编码,即:第一步将该项类别特征用数字代替,每一位数字对应一个类别特征的具体值,例如上面性别这一项,将男对应为1,将女对应为0。第二步,假设该项类别特征有\(K\)种不一样的取值,那么就设置一个长度为\(K\)的向量\(\bf k\)。对每个具体的值,假设其在第一步被编码为\(i, i \in \{0, 1, \ldots, K-1\}\),将这个\(\bf k\)的其它项设为0,但是把第\(i\)项设为1。这样,如果样本中”性别“这一列的值是”男“,送进模型之前性别这部分的向量应该是[0, 1];如果是”女“,则应该是[1, 0])
C&RT算法在具体实现时还会对缺失值进行处理。假设有一个分枝条件是\(b({\bf x}) = [\![{\rm weight \le 50kg}]\!]\),但是某些样本没有获取到体重的具体值,应该怎么办?在训练时,C&RT算法会使用一种叫做“替代分枝”(surrogate branch)的方法,即它会寻找一些类似的条件来做近似的分枝判断,例如它可能会使用高度是否小于等于155cm来代替判断体重是否小于等于50kg,而替代特征的选择也会在训练时学习到。其原理是,替代分枝\(b_1({\bf x}), b_2({\bf x})\)等等的分枝效果应该跟最优的分枝效果近似
决策树实战
概括了C&RT算法的好处:解释性强,能比较容易地处理多类别问题、离散特征、缺失特征,而且可以非常有效地训练出一个非线性模型。机器学习里几乎没有其它的模型可以同时具有以上优点
除了C&RT算法,其它决策树算法还包括C4.5和ID3算法,它们使用了一些不同的启发式算法
