最大间隔分离超平面
前面在介绍感知机时,曾经提到线性分类器的表现形式为 \[ h({\bf x}) = {\rm sign}({\bf w}^\mathsf{T}{\bf x}) \] 它在二维空间表现为一条直线,在三维空间表现为一个平面,在\(n\)维空间其维度总为\(n-1\),称作超平面
感知机算法对一个线性可分的数据集,总能找到一个超平面将其分开。然而,绝大多数情况下,这个超平面都有很多种可能性。例如下图所示

对图中的四个点,至少有三条直线可以将它们分开。PLA算法的选择是随机的,所以它们都有可能被选到。而且就VC维来看,这三条线也没什么差别。因为有 \[ E_{\rm out}({\bf w}) \le E_{\rm in}({\bf w}) + \Omega(\mathcal{H}) \] 对这三条直线,都有\(E_{\rm in}({\bf w}) = 0\)。而感知机的假设集合前面已经证明过其VC维为\(d_{\rm vc}=d+1\)。所以它们的\(E_{\rm out}\)上限是相等的
不过,对大部分人来说,可能都会选择第三幅小图中的那一个分类器。从直觉来说,假设原始数据为\({\bf x}_n\),测试数据为\({\bf x}\),由于误差的存在,有\({\bf x} \approx {\bf x}_n\)。学习的目标当然是希望对于学习出来的分类器能将这两条数据归为一类。对于图中所给出的第三个分类器,因为它离所有四个数据点都很远,因此即便这个误差比较大,它也能做出正确的分类。对每条数据,以其为圆心,用灰色标记出分类器可允许的最大误差范围(即测试点落在灰圈之内就可以得到正确的标记),三条直线各自的允许误差如下图所示

也就是说,左边分类器与最右边分类器的最大区别,就是对误差的容忍度有不同。数据\({\bf x}_n\)离分类器越远,模型对误差的容忍度越高。而由前面的讲述,测量误差是噪声的一种,因此模型对误差的容忍度越高,意味着模型对噪声的容忍度越高。又因为噪声的存在是导致过拟合现象的一大诱因,所以模型对噪声的容忍度越高,其本身鲁棒性越强,越不容易过拟合。上面的推理过程反过来也成立,所以最右分类器最优的原因是它最鲁棒,因为它离与它最近的数据最远
前面的讲述是从“点到直线距离”这个角度出发。可以换个角度,再看看从“直线到点距离”这个角度出发有什么结论。如果直线到点的距离越大,那么将直线像两边样本方向移动(直到碰到最接近的正/负例样本),其可移动的距离就越大,可以说这条直线越“胖”。三条直线各自的“胖度”如下图所示
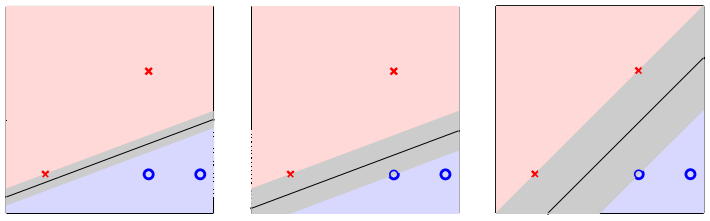
因此,分类器“越胖”,它与离它最近的数据点\({\bf x}_n\)距离越大,鲁棒性越好。我们的目标也就变成了要寻找最胖的分离超平面。假设数据集是线性可分的,那么要解决的最优化问题可以使用如下不严格的语言描述 \[ \begin{align*} \max_{\bf w} \hspace{3ex}&{\rm fatness}({\bf w}) \\ {\rm subject\ to}\hspace{3ex} &{\bf w}{\rm\ classifies\ every\ }({\bf x}_n, y_n){\rm\ correctly} \\ &{\rm fatness}({\bf w}) = \min_{n=1,\ldots,N}{\rm distance}({\bf x}_n, {\bf w}) \end{align*} \] 文献中,这个“胖度”(fatness)通常称为间隔(margin)(有点像排版中“留白”的意味)。另外,“分类正确”意味着\({\bf w^\mathsf{T}x}_n\)与\(y_n\)同号,也就是对每个样本\(n\)有\(y_n{\bf w^\mathsf{T}x}_n > 0\)。因此上面的最优化问题可以写成 \[ \begin{align*} \max_{\bf w} \hspace{3ex}&{\rm margin}({\bf w}) \\ {\rm subject\ to}\hspace{3ex} &{\rm every\ }y_n{\bf w^\mathsf{T}x}_n > 0 \\ &{\rm margin}({\bf w}) = \min_{n=1,\ldots,N}{\rm distance}({\bf x}_n, {\bf w}) \end{align*} \] 问题的目标就变成了:要找到最大间隔分离超平面
标准的最大间隔问题
由上一节最优化问题的定义,可以看到里面有一项是要计算点\({\bf x}_n\)与\(\bf{w}\)之间的距离。所以首先要解决的问题是,这个距离应该如何计算。注意这里算距离时截距项的系数\(w_0\)与其它特征项的系数\(w_1, \ldots, w_d\)是分开计算的,即 \[ \begin{align*} b &= w_0 \\ \left[\begin{array}{c} | \\ {\bf w}\\ | \end{array}\right] &= \left[\begin{array}{c}w_1 \\ \vdots \\ w_d\end{array}\right] ; \left[\begin{array}{c} | \\ {\bf x} \\ | \end{array}\right] = \left[\begin{array}{c}x_1 \\ \vdots \\ x_d\end{array}\right] \end{align*} \] 本讲中的假设函数形式也变为了 \[ h({\bf x}) = {\rm sign}({\bf w^\mathsf{T}x} + b) \] 因此要求解的问题可以定义为
给定超平面\({\bf w^\mathsf{T}x'} + b=0\),求距离\({\rm distance}({\bf x}, b, {\bf w})\)
假设\(\bf x', x''\)是超平面上的两个点,由上面的式子,显然有\({\bf w^\mathsf{T}x'} = -b, {\bf w^\mathsf{T}x''} = -b\)。两者相减,有\({\bf w^\mathsf{T}(x''-x')} = 0\)。而\(\bf x''-x'\)是超平面上的一个向量,\(\bf w\)与这个向量内积为0,说明\(\bf w\)与这个超平面正交。因此空间内任意一点\(\bf x\)到该超平面的距离就是\({\bf x - x'}\)往\(\bf w\)方向的投影,即 \[ {\rm distance}({\bf x}, b,{\bf w}) = \left|\frac{ {\bf w}^\mathsf{T}}{|\!|{\bf w}|\!|}({\bf x - x'})\right| = \frac{1}{|\!|{\bf w}|\!|}|{\bf w^\mathsf{T}x} +b| \] 又因为现在研究的超平面是分离超平面,前面提到过,在数据集线性可分的情况下,分离超平面对数据集中每个点\(n\)都有\(y_n({\bf w^\mathsf{T}x}_n + b) > 0\)且\(y_n = \pm1\)。利用这个性质,距离的计算公式又可以写为 \[ {\rm distance}({\bf x_n}, b,{\bf w}) = \frac{1}{|\!|{\bf w}|\!|}y_n({\bf w^\mathsf{T}x}_n +b) \] 又考虑到平面上同一条线有不同的表示方式,\({\bf w^\mathsf{T}x}+b = 0\)和\(3{\bf w^\mathsf{T}x} + 3b=0\),因此系数可以放缩。如果将其放缩到满足\(\min_{n=1,\ldots,N}y_n({\bf w^\mathsf{T}x}_n + b) = 1\),代入到最开始要求解的最优化问题中的限制条件,就有\({\rm margin}(b, {\bf w}) = \frac{1}{|\!|{\bf w}|\!|}\)。因此该最优化问题就可以写为 \[ \begin{align*} \max_{ {\bf w}, b} \hspace{3ex}&\frac{1}{|\!|{\bf w}|\!|}\\ {\rm subject\ to}\hspace{3ex} &{\rm every\ }y_n{\bf w^\mathsf{T}x}_n > 0 \\ &\min_{n=1,\ldots,N}y_n({\bf w^\mathsf{T}x}_n + b) = 1 \end{align*} \] 而且再仔细分析,两个限制条件中第二个条件比第一个严格,所以可以继续化简 \[ \begin{align*} \max_{ {\bf w}, b} \hspace{3ex}&\frac{1}{|\!|{\bf w}|\!|}\\ {\rm subject\ to}\hspace{3ex} &\min_{n=1,\ldots,N}y_n({\bf w^\mathsf{T}x}_n + b) = 1 \end{align*} \] 这个问题是求最大值,而限制条件里又有最小值,还是不太好解。但是限制条件可以进一步放宽,只需要满足\(y_n({\bf w^\mathsf{T}x}_n + b) \ge 1\)就可以。这里不用担心出现所有点都\(y_n({\bf w^\mathsf{T}x}_n + b) > 1\)的情况,因为如果这种情况发生,假设有\(y_n({\bf w^\mathsf{T}x}_n + b) \ge C, C > 1\),那么对\((b, {\bf w})\)缩放,得到\((b/C, {\bf w}/C)\),则还可以满足\(y_n({\bf w^\mathsf{T}x}_n + b) \ge 1\),但是因为\(\bf w\)被除了一个大于1的正常数,因此\(\frac{1}{|\!|w|\!|}\)会变大,新的解比\((b, {\bf w})\)取得的最优解更好,造成矛盾。最后,再做一点简单的变换,可以得到最终要优化的问题为 \[ \begin{align*} \min_{ {\bf w}, b} \hspace{3ex}&\frac{1}{2}{\bf w^\mathsf{T}w}\\ {\rm subject\ to}\hspace{3ex} &y_n({\bf w^\mathsf{T}x}_n + b) \ge 1{\rm\ for\ all\ }n \end{align*} \]
支持向量机(SVM)
上面得到的这个问题通常称为标准问题,解这个问题返回的\(g\)通常称为支持向量机(Support Vector Machine, SVM)。SVM的来源是这样的:通过分析第一节中的例子,可以发现最大间隔分离超平面完全由离该超平面最近的点定义,其它点如果从数据集中删除掉,对最优超平面的选择没有任何影响。这些决定了最大间隔分离超平面的点通常被称为支持向量,因此SVM的意思就是使用支持向量学习出最优的超平面
SVM并不是一个很容易手工解出的问题。由于限制条件的存在,使用梯度下降也不太方便。不过这个问题要最小化的是一个\(\bf w\)的二次函数,限制条件又都是\({\bf w}\)和\(b\)的一次式,因此这个问题其实是凸优化问题里的二次规划问题(简称QP问题)。接下来的问题就是,如何把这个最优化问题改写成二次规划问题的标准形式。假设变量为\(\bf u\),其二次项系数为\(\rm Q\),一次项系数为\(\bf p^\mathsf{T}\),限制条件的每一项系数为\({\bf a}_m^\mathsf{T}\),常数为\(c_m\),则二次规划问题的标准形式就可以写为 \[ {\rm optimal\ }{\bf u} \leftarrow {\rm QP}({\rm Q}, {\bf p}, {\rm A}, {\bf c}) \\ \begin{align*} \min_{\bf u} & \hspace{3ex}\frac{1}{2}{\bf u}^\mathsf{T}{\rm Q}{\bf u} + {\bf p^\mathsf{T}u} \\ {\rm subject\ to} & \hspace{3ex}{\bf a}_m^\mathsf{T}{\bf u} \ge c_m, {\rm for\ }m =1,2,\ldots, M \end{align*} \] 记\(\bf w\)的维数为\(d\),则对应关系如下 \[ \begin{align*} {\bf u} &= \left[\begin{array}{c}b \\ {\bf w}\end{array}\right] \\ {\rm Q} &= \left[\begin{matrix} 0 & {\bf 0}_d^\mathsf{T} \\ {\bf 0}_d & {\rm I}_d\end{matrix}\right] \\ {\bf p} &= {\bf 0}_{d+1} \\ {\bf a}_n^\mathsf{T} &= y_n\left[\begin{array}{c}1 & {\bf x}_n^\mathsf{T}\end{array}\right] \\ c_n &= 1 \\ M &= N \end{align*} \] 因此可以得到线性硬间隔支持向量机算法为
- 设置\({\rm Q} = \left[\begin{matrix} 0 & {\bf 0}_d^\mathsf{T} \\ {\bf 0}_d & {\rm I}_d\end{matrix}\right];{\bf p} = {\bf 0}_{d+1};{\bf a}_n^\mathsf{T} = y_n\left[\begin{array}{c}1 & {\bf x}_n^\mathsf{T}\end{array}\right] ;c_n = 1\)
- \(\left[\begin{array}{c} b \\ {\bf w}\end{array}\right] \leftarrow {\rm QP}({\rm Q}, {\bf p}, {\rm A}, {\bf c})\)
- 将\(b\)和\(\bf w\)返回为\(g_{\rm SVM}\)
这里“硬间隔”意味着没有点会在“胖的边界”里或者甚至越过分离超平面,而“线性”意味着用的是原始的\(\bf x\)。如果要做非线性的SVM,只需要做非线性转换\({\bf z}_n = \boldsymbol{\Phi}({\bf x}_n)\)就可以
最大间隔分离超平面背后的原理
最后,来看一下SVM模型可以做得好的理论解释:SVM可以跟正则化做连接:正则化最小化的是\(E_{\rm in}\),但是限制了\({\bf w^\mathsf{T}w} \le C\),而SVM最小化的是\({\bf w^\mathsf{T}w}\),限制条件是\(E_{\rm in} = 0\)(当然还有其它条件,但是这里没有包括进去)。尽管两者的最小化目标和限制条件有所交换,但是可以认为两者做的事情是相同的,实际上就是想把两件事都考虑进去,即可以把SVM看作是一种正则化
另一种解释是从VC的角度看。假设现在使用一种“大间隔算法”\(\mathcal{A}_\rho\),如果存在某个\(g\)有\({\rm margin}(g) \ge \rho\),则这个算法返回\(g\),否则返回空。\(\mathcal{A}_0\)(实际上就是PLA)可以打散三个元素,但是如果\(\rho\)比较大,能被\(\mathcal{A}_0\)打散的数据就不一定能被\(\mathcal{A}_\rho\)打散。即SVM的VC维更小,一般化能力更强
可以从概念上推导\(\mathcal{A}_\rho\)的VC维,注意此时VC维依赖于数据。这里假设\(\mathcal{X}\)是\(\mathbb{R}^2\)上的单位圆,如果\(\rho=0\),那算法退化成感知机,\(d_{\rm VC} = 3\)。但是当\(\rho > \frac{\sqrt{3}}{2}\)时,算法不能打散任何3个输入,\(d_{\rm VC} < 3\)。通常来讲,假设\(\mathcal{X}\)在一个半径为\(R\)的超球体里,有 \[ d_{\rm VC}(\mathcal{A}_\rho) \le \min \left(\frac{R^2}{\rho^2}, d\right) + 1 \le d+1 \] 之前课程讲述过超平面和特征变换这两种工具。超平面的假设集不大,但是边界比较简单;而带了特征变换的超平面的假设集变得非常大,不过边界也更加复杂。这两者颇有点鱼和熊掌的意味:假设集不大是件好事,因为\(d_{\rm VC}\)不会太大,有利于一般化;边界复杂也是好事,因为这会使\(E_{\rm in}\)变小。在之前,这两种优点不可兼得,但是SVM的引入使得这两个好处有可能被一个模型同时获得(因为SVM的假设集更小)。这种模型称为非线性SVM,其使用的还是SVM的思想,但是会对数据做一些特征变换\(\boldsymbol{\Phi}\)
