模型选择问题
即便是对二元分类问题,前面也介绍了很多种机器学习算法。这些算法(和算法所需要设置的参数)包括了
- 算法\(\mathcal{A}\)本身,例如PLA、口袋算法、线性回归、Logistic回归
- 算法迭代的步数\(T\)。是100,1000还是10000
- 算法的学习率\(\eta\)。是1,0.1还是0.01
- 特征转换\(\boldsymbol{\Phi}\)。是原始的特征,线性的特征,10次特征还是勒让德多项式10次特征
- 正则项\(\Omega({\bf w})\)。是L2正则项,L1正则项还是其它正则项
- 正则项系数\(\lambda\)。是0,0.01还是1
既然面对了这么多选择,应该如何做决策就成了一个问题,这种问题称为模型选择问题。其可以进一步描述为,给定\(M\)个模型\(\mathcal{H}_1, \mathcal{H}_2, \ldots, \mathcal{H}_M\),每个模型对应的算法为\(\mathcal{A}_1, \mathcal{A}_2, \ldots, \mathcal{A}_M\),选出一个模型\(\mathcal{H}_{m ^ \ast}\)使得\(g_{m^\ast} = \mathcal{A}_{m^\ast}(\mathcal{D})\)有比较低的\(E_{\rm out}(g_{m^\ast})\)。这个问题的难点在于,由于无法知道\(P({\bf x})\)和\(P(y|{\bf x})\),因此\(E_{\rm out}\)是未知的;而选择又是不可避免的,因此这个问题是非常有实际意义的
通过视觉方法做选择已经在第12讲被否定了。那么是否可以根据各模型的\(E_{\rm in}\)来判断?即 \[ m^\ast = \mathop{ {\rm arg} \min}_{1\le m \le M}(E_m = E_{\rm in}(\mathcal{A}_m(\mathcal{D}))) \] 并不可以。回顾之前的各种实验数据,如果采用了这样的设定,\(\boldsymbol{\Phi}_{1126}\)一定好于\(\boldsymbol{\Phi}_1\),\(\lambda=0\)肯定比\(\lambda = 0.1\)好,因此会非常容易过拟合。此外,假设\(\mathcal{A}_1\)是在\(\mathcal{H}_1\)上最小化了\(E_{\rm in}\),\(\mathcal{A}_2\)是在\(\mathcal{H}_2\)上最小化了\(E_{\rm in}\),那么最优的\(g_{m^\ast}\)就会在\(\mathcal{H}_1 \cup \mathcal{H}_2\)上最小化\(E_{\rm in}\),模型选择和学习的过程VC维就是\(d_{\rm VC}(\mathcal{H}_1 \cup \mathcal{H}_2)\)。VC维变大,就会导致一般化问题
综上所述,使用\(E_{\rm in}\)选择模型是非常危险的
或者可以根据各模型在测试集上的表现\(E_{\rm test}\)来判断?即 \[ m^\ast = \mathop{ {\rm arg} \min}_{1\le m \le M}(E_m = E_{\rm test}(\mathcal{A}_m(\mathcal{D}))) \] 这样做可以避免一般化问题,因为根据有限的Hoeffding不等式,有 \[ E_{\rm out}(g_{m^\ast}) \le E_{\rm test}(g_{m^\ast}) + O\left(\sqrt{\frac{\log M}{N_{\rm test}}}\right) \] 但这么做的问题是,测试数据应该是找不到的,或者它应该在你老大那里!所以,这种方法是不可行的,至少是自欺欺人的
既然两种方法都不可行,有没有可能找到一份数据,它能同时满足以下三个要求:
- 与样本\(\mathcal{D}\)中数据独立同分布
- 方便获得
- 干净,没有被\(\mathcal{A}_m\)用来选择\(g_m\)(没有被候选算法偷看过)
答案是肯定的。具体做法是从原始数据中划出一部分数据作为验证数据(或者称为验证集),记为\(\mathcal{D}_{\rm val}\)。然后,将算法用在\(\mathcal{D}_{\rm val}\)上,根据它们在这些数据上的错误\(E_{\rm val}\)来选择模型(有点像是合法地作弊)
验证
前面说到,可以从原始数据\(\mathcal{D}\)中取一部分数据作为验证数据\(\mathcal{D}_{\rm val}\),即有\(\mathcal{D}_{\rm val} \subset \mathcal{D}\),用它来模拟测试集。假设验证集大小为\(K\),为了让验证误差\(E_{\rm val}\)能够逼近\(E_{\rm out}\),这\(K\)个数据需要随机从\(\mathcal{D}\)中抽取。这样,原始大小为\(N\)的数据集被分解成了互不相交的两个集合:大小为\(N-K\),专门用来做训练的数据集\(\mathcal{D}_{\rm train}\)和大小为\(K\) ,专门用来做验证的验证集\(\mathcal{D}_{\rm val}\)。为了保证\(\mathcal{D}_{\rm val}\)的纯洁性,只能把\(\mathcal{D}_{\rm train}\)送进算法\(\mathcal{A}_m\)去训练模型和做模型选择。记通过这种方法得到的最优假设为\(g^-_m\),类比前面给出的不等式,有 \[ E_{\rm out}(g_{m}^-) \le E_{\rm val}(g_{m}^-) + O\left(\sqrt{\frac{\log M}{K}}\right) \] 因此,模型选择的方法是 \[ m^\ast = \mathop{ {\rm arg} \min}_{1\le m \le M}(E_m = E_{\rm val}(\mathcal{A}_m(\mathcal{D}_{\rm train}))) \] 但是这里有一点需要注意:验证集的分出意味着与原来相比训练集变小。由之前的学习曲线可知,使用更少数据训练出来的模型,其\(E_{\rm out}\)会大。因此,合理做法是记录\(m^\ast\)对应模型的超参数(就是前面提到的\(\lambda, \boldsymbol{\Phi}\)等等),然后用整个\(\mathcal{D}\)再把该模型训练一遍
可以使用验证的方法来在五次多项式特征变换假设集\(\mathcal{H}_{\boldsymbol{\Phi}_5}\)和十次多项式特征变换假设集\(\mathcal{H}_{\boldsymbol{\Phi}_{10}}\)之间做选择。得到的图像如下图所示
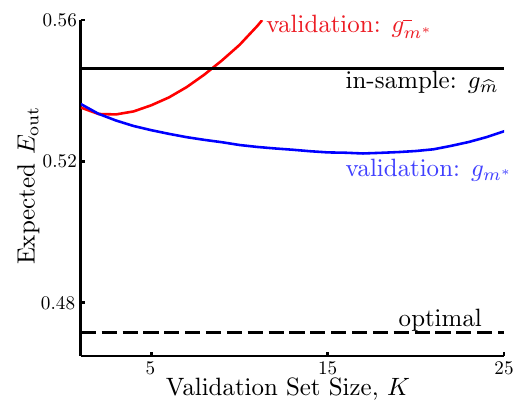
这里四条线分别为:
- 黑实线,表示使用\(E_{\rm in}\)来做选择,得到的最优模型的\(E_{\rm out}\)。记该模型为\(g_{\hat{m}}\)
- 黑虚线(很靠下可能容易被忽略掉),表示使用\(E_{\rm test}\)来做选择,得到的最优模型的\(E_{\rm out}\)(实际上是作弊了)
- 红实线,表示使用\(\mathcal{D}_{\rm train}\)训练,\(\mathcal{D}_{\rm val}\)做模型选择得到的最优模型的\(E_{\rm out}\)。记该模型为\(g_{m^\ast}^-\)
- 蓝实线,表示使用\(\mathcal{D}_{\rm train}\)训练,\(D_{\rm val}\)做模型选择,然后再把最优模型用\(\mathcal{D}\)训练一遍得到的模型的\(E_{\rm out}\)。记该模型为\(g_m^\ast\)
可见蓝实线总是最低的,因此验证法真的在实际工程中可用
注意红线不如黑线的状况是因为\(K\)比较大,因此用来训练模型的数据量变小,所以模型效果就不好了。这也说明在选择验证集大小的时候其实有个两难境地:如果要使\(E_{\rm out}(g) \approx E_{\rm out}(g^-)\),就需要\(K\)比较小才好,因为有足够多的数据训练模型;而要想\(E_{\rm out}(g^-) \approx E_{\rm val}(g^-)\),就需要\(K\)比较大才好,因为这样才能足够模拟未知情况。实际中,常常设\(K = N/5\)
留一交叉验证
对于上面的验证过程,考虑一个极端情况:\(K=1\)。这样,\(g^-\)和\(g\)会非常接近,但是\(E_{\rm out}(g^-) \approx E_{\rm val}(g^-)\)就不能满足了,只有一条数据能够用来验证模型。假设这条数据是第\(n\)条数据,则 \[ \begin{align*} \mathcal{D}_{\rm val}^{(n)} &= \{({\bf x}_n, y_n)\} \\ E_{\rm val}^{(n)}(g_n^-) &={\rm err}(g_n^-({\bf x}_n), y_n) = e_n \end{align*} \] 这一条\(e_n\)显然不能管中窥豹,很好地近似\(E_{\rm out}(g)\)(事实上,如果要解决的是一个二元分类问题,使用一条数据得到的误差值只可能是0或者1,不可能是一个浮点数)。但是,如果验证的过程重复\(n\)遍,依次取出一条数据作为验证集,将它们的\(e_n\)记录下来最后做平均,得到的平均误差可能就是对\(E_{\rm out}\)一个很好的近似。记这个过程为留一交叉验证,则该过程对\(E_{\rm out}\)的近似为 \[ E_{\rm loocv}(\mathcal{H, A}) = \frac{1}{N}\sum_{n=1}^Ne_n = \frac{1}{N} \sum_{n=1}^N {\rm err}(g_n^-({\bf x}_n), y_n) \] 接下来就是要证明,确实有\(E_{\rm loocv}(\mathcal{H, A}) \approx E_{\rm out}(g)\)。设假设集\(\mathcal{H}\)和算法\(\mathcal{A}\)在任意数据集上都用过,所有这些数据集的期望留一交叉验证误差为\(\mathcal{E}_{\mathcal{D}}E_{\rm loocv}(\mathcal{H, A})\),则 \[ \begin{align*} \mathcal{E}_{\mathcal{D}}E_{\rm loocv}(\mathcal{H, A}) =\mathcal{E_D}\frac{1}{N}\sum_{n=1}^Ne_n &= \frac{1}{N}\sum_{n=1}^N\mathcal{E_D}e_n \\ &= \frac{1}{N}\sum_{n=1}^N\mathcal{E}_{\mathcal{D}_n}\mathcal{E}_{({\bf x}_n, y_n)} {\rm err}(g_n^-({\bf x}_n), y_n) \\ &= \frac{1}{N}\sum_{n=1}^N\mathcal{E}_{\mathcal{D}_n}E_{\rm out}(g_n^-) \\ &= \frac{1}{N}\sum_{n=1}^N\overline{E_{\rm out}}(N-1) = \overline{E_{\rm out}}(N-1) \end{align*} \] 即留一交叉验证误差的期望值与\(E_{\rm out}(g^-)\)的期望值的确是近似的,可以看作是\(E_{\rm out}(g)\)几乎无偏差的估计
下图给出了留一交叉验证的一个示例
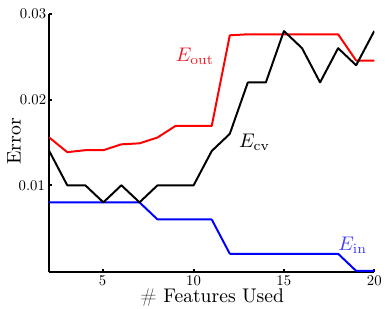
可以看出,交叉验证的误差曲线和\(E_{\rm out}\)非常接近,即在实践中它的确是对\(E_{\rm out}\)一个很好的估计。这张图再次证明,过多的特征会导致过拟合,特征数适量最好
\(V\)折交叉验证
留一交叉验证虽然可以很好地估计\(E_{\rm out}\),但是耗费的时间太多:每次使用\(N-1\)条数据训练,重复\(N\)次。因此除非有个别情况(例如有解析解的情况),否则留一交叉验证不太可行。此外,这种方法还有稳定性的问题。可以看到前一节的图中\(E_{\rm cv}\)曲线有波动,而我们都希望选择的模型是比较可靠的,并不是因为某个实验的波动才导致其\(E_{\rm cv}\)变小
思考留一交叉验证的过程可以发现,计算量变大的主要原因是该方法把数据集切得太碎,验证集太小造成了计算量的增加。因此一个改进的方法就是,只把原始数据集“斩成几大块”。这种方法叫做\(V\)折交叉验证:原始数据集\(\mathcal{D}\)被随机分成\(V\)份,仍然是每次使用\(V-1\)份数据训练模型,1份数据用来验证。这里交叉验证的误差为 \[ E_{\rm cv}(\mathcal{H, A}) = \frac{1}{V}\sum_{v=1}^V E_{\rm val}^{(v)}(g_v^-) \] 选择时,仍然是 \[ m^\ast = \mathop{ {\rm arg}\min}_{1 \le m \le M} (E_m = E_{\rm cv}(\mathcal{H}_m , \mathcal{A}_m)) \] 实践中,\(V\)通常设为10
总结
实践中,如果计算允许的话,一般还是使用\(V\)折交叉验证,而不使用普通的单次验证。而且5折交叉验证或者10折交叉验证效果就不错了,没必要做留一交叉验证
训练模型的过程是在整个假设集上做选择,有点像初赛;而验证的过程是对初赛中选出来的模型再做一次选择,有点像复赛。需要注意的是,只要有选择就会有误差,因此验证的结果还是会比测试结果更乐观。测试结果才是最重要的,不要用验证结果自欺欺人
