感知机假设集合
上回说到机器学习的核心就是,使用算法\(\mathcal{A}\)接收数据\(\mathcal{D}\),从假设集合(所有可能性)\(\mathcal{H}\)中选出一个\(g\),希望\(g \approx f\)。那么我们现在最关心就是,\(\mathcal{H}\)应该是什么样的。
以之前提到的银行审核发放信用卡的场景为例,假设我们把每个使用者定义为向量\(\bf x\),包含\(d\)个维度,例如\(x_1\)代表年龄,\(x_2\)代表年薪,等等。我们可以将这些维度(因素)综合起来给使用者一个整体分数。如果这个分数超过了某个标准,那就给ta发放;否则拒绝发放。这样,我们需要给每个\(x_i, i \in \{1, \ldots, d\}\)来赋一个系数\(w_i\),如果特征对最后的影响是正面的,那么就给\(w_i\)正值,否则给负值。如果我们再规定一个阈值\(\rm threshold\),那么我们的决策方法就可以写为,如果\(\sum_{i=1}^d w_ix_i > {\rm threshold}\),就批准信用卡申请,否则就拒绝。
我们可以进一步地规定输出空间\(\mathcal{Y} \in \{-1, +1\}\),其中\(y = -1\)时表示拒绝,\(y=1\)时表示许可。这样做的好处是我们可以直接使用\(\rm sign\)函数来求出\(y\)的值,具体地说,假设集合\(\mathcal{H}\)中的每个元素\(h \in \mathcal{H}\)都有如下形式 \[ h({\bf x}) = {\rm sign}\left(\left(\sum_{i=1}^d w_ix_i\right) - {\rm threshold}\right) \] 其中\(\rm sign\)函数的定义为 \[ {\rm sign}(x) = \begin{cases} +1 & {\rm if\ } x > 0 \\ -1 & {\rm if\ }x < 0\end{cases} \] 即对用户的所有属性做一个加权打分,看它是否超过阈值。如果超过,则批准;否则就拒绝(如果正好等于阈值,这种情况很少发生,甚至可以随机决定\(y\)是-1还是1)。
这里我们说\(\mathcal{H}\)是一个集合的原因是,不同的\(\bf w\)和\(\rm threshold\)都对应了不同的\(h\),所有这些可能性对应的所有\(h\)构成了最后的假设集合\(\mathcal{H}\)。\(h\)这样的函数类型称为感知机(perceptron),其中\(\bf w\)称为权重。进一步地,假设我们把\(-\rm threshold\)看做是\((-{\rm threshold}) \cdot (+1)\),然后把\(+1\)看作是\(x_0\),那么前面的公式形式可以作进一步的简化,即 \[ \begin{align*} h({\bf x}) &= {\rm sign}\left(\left(\sum_{i=1}^d w_ix_i\right) - {\rm threshold}\right) \\ &= {\rm sign}\left(\left(\sum_{i=1}^d w_ix_i\right) + \underbrace{(- {\rm threshold})}_{w_0}\cdot \underbrace{(+1)}_{x_0}\right) \\ &= {\rm sign}\left(\sum_{i=0}^d w_ix_i\right) \\ &= {\rm sign}({\bf w}^\mathsf{T}{\bf x}) \end{align*} \] 这里\(\bf w\)和\(\bf x\)都看作是列向量,即维度为$ (d+1) 1$
我们可以来看一个图例来加强理解。假如我们顾客的特征数(也就是前面说的属性维度)为2,那么我们可以把任意输入\(\bf x\)画在一个平面\(\mathbb{R}^2\)上(类似的,如果特征数为\(d\),那么每个输入\(\bf x\)都可以在\(\mathbb{R}^d\)空间表示,只是会对我们的可视化造成困难),每个输入对应平面上的一个点。这样,\(\mathbb{R}^2\)上的\(h\)都有如下形式: \[ h({\bf x}) = {\rm sign}(w_0 + w_1x_1 + w_2x_2) \] 可以看出,每个\(h\)其实都对应了\(\mathbb{R}^2\)上的一条直线。感知机规定位于直线某一侧的样本都被判定为正例,另一侧的样本都被判定为负例。不同的权重会产生不同的直线,从而对顾客有不同的分类方式。假设我们用蓝色的圈o表示正例,红色的叉×表示负例,下图给出了两个不同感知机的图
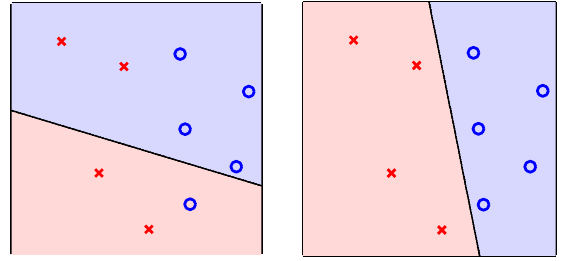
可以看出右边的感知机在训练集上效果更好,因为它对所有例子做出了正确分类。而左侧的感知机在训练集上表现稍逊(一个正例被误判为负,两个负例被误判为正)
由于感知机都对应于一个超平面,因此它也被称为是线性分类器(\(\mathbb{R}^2\)的超平面是一条直线,\(\mathbb{R}^3\)的超平面是一个平面,以此类推)。
感知机学习算法
在我们知道了\(h \in \mathcal{H}\)的形态以后,接下来的问题是设计算法\(\mathcal{A}\)来选出最优的\(g\)来逼近理想的\(f\)。尽管我们不知道\(f\)具体应该是什么,但是我们知道数据\(\mathcal{D}\)是由\(f\)生成。因此我们有理由相信,好的\(g\)满足对所有我们已经收集到的数据,其输出与\(f\)的输出尽可能接近,即\(g({\bf x}_n) = f({\bf x}_n) = y_n\)。因此,我们可以先找一个超平面,至少能够对训练集中的数据正确分类。然而难度在于,\(\mathcal{H}\)的大小通常都是无限的。
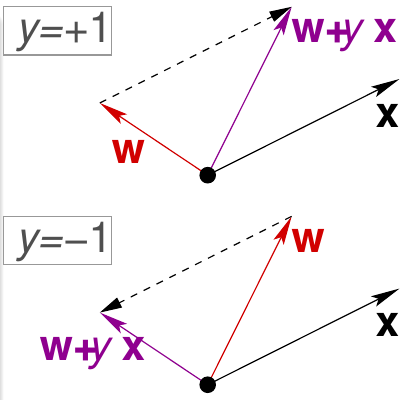
一种解决方案是,我们可以先初始化一个超平面\(g_0\)(为了简单起见,将其以其权重\({\bf w}_0\)代表,称为初始权重)。我们允许这个超平面犯错,但是我们要设计算法,让超平面遇到\(\mathcal{D}\)中的错分样本以后可以修正自己。通常我们可以将\({\bf w}_0\)初始化为零向量\(\bf 0\)。然后,在每一步\(t\),找到一个使\({\bf w}_t\)错分的样本\(({\bf x}_{n(t)}, y_{n(t)})\)。即有 \[ {\rm sign}({\bf w}_t^\mathsf{T}{\bf x}_{n(t)}) \not =y_{n(t)} \] 接下来我们试着修正\({\bf w}_t\)。可以看到错分有两种情况:
- \(y\)本来应该是+1,但是模型判断出来是负值。也就是说此时\(\bf w\)与\(\bf x\)之间的角度太大,因此需要把\(\bf w\)往靠近\(\bf x\)的方向旋转使它们的角度变小。可以通过让\({\bf w}_{t+1} \leftarrow {\bf w}_t + y_{n(t)}{\bf x}_{n(t)}\)达到这个目的
- \(y\)本来应该是-1,但是模型判断出来是正值。也就是说此时\(\bf w\)与\(\bf x\)之间的角度太小,因此需要把\(\bf w\)往远离\(\bf x\)的方向旋转使它们的角度变大。考虑到符号,其实也可以通过让\({\bf w}_{t+1} \leftarrow {\bf w}_t + y_{n(t)}{\bf x}_{n(t)}\)达到这个目的
因此,在第\(t+1\)时刻,我们总可以通过下式来修正\({\bf w}_t\),即 \[ {\bf w}_{t+1} \leftarrow {\bf w}_t + y_{n(t)}{\bf x}_{n(t)} \] 下图给出了这两种情况的示例
感知机学习算法(Perceptron Learning Algorithm, PLA)就是重复上面的过程,直到没有错误发生为止。算法将最后得到的权重\(\bf w\)(记做\({\bf w}_{\rm PLA}\))返回为\(g\)。完整的写法如下
感知机学习算法
对\(t = 0, 1, \ldots\)
1). 找到一个使\({\bf w}_t\)错分的样本\(({\bf x}_{n(t)}, y_{n(t)})\)。即有 \[ {\rm sign}({\bf w}_t^\mathsf{T}{\bf x}_{n(t)}) \not =y_{n(t)} \]
2). 以如下方法修正\({\bf w}_t\): \[ {\bf w}_{t+1} \leftarrow {\bf w}_t + y_{n(t)}{\bf x}_{n(t)} \] 直到遍历了所有样本一遍以后都没有找到错误为止。
注意这里“遍历一遍”不一定非得顺序遍历,只要遍历过样本的一个全排列即可。例如假如样本中有4条数据,可以按照诸如2,3,4,1或者3,2,1,4这样的顺序遍历
讲到这里,我们可能会有以下问题:
- 算法真的会停止吗?
- 能否确定算法返回的\(g \approx f\)?
我们接下来会讨论这些问题。不过我在这里想首先对Fun time中的题目做一个详细解答。为了方便起见,简记\(y = y_{n(t)}, {\bf x} = {\bf x}_{n(t)}, {\bf w} = {\bf w}_t\),代入\({\bf w}_{t+1} \leftarrow {\bf w}_t + y_{n(t)}{\bf x}_{n(t)}\),有 \[ \begin{align*} y{\bf w}_{t+1}^\mathsf{T}{\bf x} &= y({\bf w} + y{\bf x})^\mathsf{T}{\bf x} \\ &= (y{\bf w}^\mathsf{T} + y(y{\bf x})^\mathsf{T}){\bf x} \\ &= y{\bf w}^\mathsf{T}{\bf x} + y{\bf x}^\mathsf{T}y^\mathsf{T}{\bf x} \\ &= y{\bf w}^\mathsf{T}{\bf x} + yy^\mathsf{T}{\bf x}^\mathsf{T}{\bf x} \hspace{3ex} (\because y {\rm\ is\ a\ scalar}) \\ &= y{\bf w}^\mathsf{T}{\bf x} + y^2|\!|{\bf x}|\!|_2^2 > y{\bf w}^\mathsf{T}{\bf x} \end{align*} \]
感知机的有效性与确定终止性
回顾PLA算法的停止条件,它是在没有找到错误的时候才停止,这要求我们的数据可以用一条线将正例样本和负例样本分割开来(如果不存在这条线,PLA肯定是不可能停止的)。这种条件叫做线性可分条件。接下来,我们需要证明:如果数据集的确是线性可分的,感知机是否总能找到一个超平面把数据恰好分开。
假设数据集\(\mathcal{D}\)线性可分,我们先证明存在一个超平面\({\bf w}_f\)使得对任意\(i \in \{1, \ldots, n\}, y_i = {\rm sign}({\bf w}_f^\mathsf{T}{\bf x}_i)\)。这意味着对每个\({\bf x}_i\),它与超平面都有一定距离,即 \[ \min_n y_n {\bf w}_f^\mathsf{T}{\bf x}_n > 0 \] 其中\({\bf w}_f^\mathsf{T}{\bf x}_n\)是点\({\bf x}_n\)到\({\bf w}_f\)的带符号的距离。如果它被放在了相对于超平面的正确一侧,那么这个值与其标签的乘积应该是正数,否则为负数。则在训练过程中遇到的所有错分点\(({\bf x}_{n(t)}, y_{n(t)})\)(假设在时刻\(t\)遇到),肯定有 \[ y_{n(t)}{\bf w}_f^\mathsf{T}{\bf x}_{n(t)} \ge \min_n y_n {\bf w}_f^\mathsf{T}{\bf x}_n > 0 \] 我们可以先证明,\({\bf w}_t\)被\(({\bf x}_{n(t)}, y_{n(t)})\)纠正以后更加接近\({\bf w}_f\)。我们可以通过两个向量的内积来判断它们是否接近:两个向量越接近,内积越大(可以理解为两向量\({\bf u}\)和\(\bf v\)越接近,其夹角\(\theta\)越小,那么\(\cos \theta\)越大,所以两者的内积\({\bf u} \cdot {\bf v} = |\!|{\bf u}|\!||\!|{\bf v}|\!|\cos \theta\)越大),则 \[ \begin{align*} {\bf w}_f^\mathsf{T}{\bf w}_{t+1} &= {\bf w}_t^\mathsf{T}({\bf w}_t + y_{n(t)}{\bf x}_{n(t)}) \\ &\ge {\bf w}_f^\mathsf{T}{\bf w}_t + \min_n y_n {\bf w}_f^\mathsf{T}{\bf x}_n \\ &> {\bf w}_f^\mathsf{T}{\bf w}_t + 0 = {\bf w}_f^\mathsf{T}{\bf w}_t\hspace{3ex}\blacksquare \end{align*} \] 但是这里有一个漏洞,即内积变大不一定说明两个向量接近,因为向量长度变大也会导致内积变大。因此接下来我们要证明,修正\({\bf w}_t\)以后,新的权重长度不会发生太大变化。这里要用到一个性质,即PLA仅在遇到错误的数据时才更新权重,即如果权重\({\bf w}_t\)被订正,意味着\({\rm sign}({\bf w}_t^\mathsf{T}{\bf x}_{n(t)}) \not= y_{n(t)}\),也就是\(y_{n(t)}{\bf w}_t^\mathsf{T}{\bf x}_{n(t)} \le 0\)。考虑到\(y_{n(t)}\)是标量,且取值只可能为1或-1(即\(y_{n(t)}^2 = 1\)),\({\bf w}_t^\mathsf{T}{\bf x}_{n(t)}\)也是标量,因此 \[ \begin{align*} |\!|{\bf w}_{t+1}|\!|^2 &= |\!|{\bf w}_t + y_{n(t)}{\bf x}_{n(t)}|\!|^2 \end{align*} \] 简记\(y = y_{n(t)}, {\bf x} = {\bf x}_{n(t)}, {\bf w} = {\bf w}_t\),则 \[ \begin{align*} |\!|{\bf w}_{t+1}|\!|^2 &= ({\bf w}+y{\bf x})^\mathsf{T}({\bf w}+y{\bf x}) \\ &= {\bf w}^\mathsf{T}{\bf w} + 2y{\bf w}^\mathsf{T}{\bf x} + {\bf x}^\mathsf{T}{\bf x} \\ &\le |\!|{\bf w}|\!|^2 + |\!|{\bf x}|\!|^2\hspace{3ex}(\because y{\bf w}^\mathsf{T}{\bf x} \le 0) \\ &\le |\!|{\bf w}|\!|^2 + \max_n |\!|{\bf x}_n|\!|^2 \end{align*} \] 即权重经过修正以后,其长度最多增加\(\max_n |\!|{\bf x}_n|\!|^2\)
经由上面两个部分,假设权重的初始向量为\(\bf 0\),我们可以求出经过\(T\)步更新最后得到的权重\({\bf w}_T\)与\({\bf w}_f\)之间的夹角余弦值的下界。为了求这个值,只需求两个权重归一化以后内积的下界即可,即 \[ \inf \left(\frac{ {\bf w}_f^\mathsf{T}}{|\!|{\bf w}_f|\!|} \cdot \frac{ {\bf w}_T}{|\!|{\bf w}_T|\!|} \right) \] 先看分子。由于初始\({\bf w}_0 = {\bf 0}\),因此由之前第一个证明的中间步骤,我们可以写出第一次更新、第二次更新……后分子的下界,即 \[ \begin{align*} {\bf w}_f^\mathsf{T}{\bf w}_1 &\ge {\bf w}_f^\mathsf{T}\cdot {\bf 0} + \min_n y_n{\bf w}_f^\mathsf{T}{\bf x}_n \\ {\bf w}_f^\mathsf{T}{\bf w}_2 &\ge {\bf w}_f^\mathsf{T}\cdot {\bf w}_1 + \min_n y_n{\bf w}_f^\mathsf{T}{\bf x}_n \ge {\bf w}_f^\mathsf{T}\cdot {\bf 0} + 2\min_n y_n{\bf w}_f^\mathsf{T}{\bf x}_n \\ &\vdots \\ {\bf w}_f^\mathsf{T}{\bf w}_T &\ge T \min_n y_n{\bf w}_f^\mathsf{T}{\bf x}_n \end{align*} \] 类似地,对分母有 \[ |\!|{\bf w}_T|\!|^2 \le T\max_n|\!|{\bf x}_n|\!|^2 \] 因此, \[ \begin{align*} \frac{ {\bf w}_f^\mathsf{T}}{|\!|{\bf w}_f|\!|} \cdot \frac{ {\bf w}_T}{|\!|{\bf w}_T|\!|} &\ge \frac{T\min_n y_n{\bf w}_f^\mathsf{T}{\bf x}_n}{|\!|{\bf w}_f|\!|\sqrt{T\max_n|\!|{\bf x}_n|\!|^2}} \\ &= \sqrt{T}\cdot \frac{\min_n y_n{\bf w}_f^\mathsf{T}{\bf x}_n}{|\!|{\bf w}_f|\!|\sqrt{\max_n|\!|{\bf x}_n|\!|^2}} \end{align*} \] 按照Fun Time中的记法,记\(R^2 = \max_n |\!|{\bf x}_n|\!|^2, \rho = \min_n y_n \frac{ {\bf w}_f^\mathsf{T}}{|\!|{\bf w}_f|\!|} {\bf x}_n\),则 \[ \frac{ {\bf w}_f^\mathsf{T}}{|\!|{\bf w}_f|\!|} \cdot \frac{ {\bf w}_T}{|\!|{\bf w}_T|\!|} \ge \sqrt{T}\cdot\frac{\rho}{R} \] 由于向量除以其长度得到的是单位向量,长度为1,在这种情况下,两者内积越大一定意味着两者的夹角越小,距离越近。但是这里需要注意的是,两者的距离不会无限接近,到\(\cos \theta=1\)时就会停止。换一个角度看,因为两个单位向量的内积最大值为1,因此从上面的不等式可推出 \[ \sqrt{T} \cdot \frac{\rho}{R} \le 1 \Rightarrow T \le \frac{R^2}{\rho^2} \] 即算法至多更新\(\frac{R^2}{\rho^2}\)步后一定会停止
感知机在线性不可分数据上的应用
由上面的证明,假设数据集是线性可分的,那么PLA算法最后肯定会停止,而且(对训练集)给出正确的分类。该算法非常容易实现,而且结束很快,适用于任意\(\mathbb{R}^d\)空间。但是这个算法最大的问题是,它要提前假设训练集是训练可分的,而且我们不知道算法什么时候会终止(因为上面给出的上限中用到了\({\bf w}_f\),而我们不知道它是多少——甚至不知道是否存在!(在线性不可分的时候该向量不存在))
那么我们来考虑一个最坏的情况,即数据若的确是线性不可分的话,应该如何应对。由于数据产生的过程中可能会混入噪声,这使得原本线性可分的数据也可能因为噪声的存在而不可分。但是,一般情况下,噪声应该是一小部分,即我们可以退而求其次,不去寻找一个完美的超平面,而是去寻找一个犯错误最少的超平面,即 \[ {\bf w}_g \leftarrow \mathop{ {\rm arg}\min}_{\bf w} \sum_{n=1}^N [\![ y_n \not= {\rm sign}({\bf w}^\mathsf{T}{\bf x}_n)]\!] \] 然而,求解这个问题被证明是NP难的,只能采用近似算法求解。例如,我们可以保存一个最好的权重,该权重到目前为止错分的数量最少。该算法称为“口袋法”,其完整细节如下
设定初始权重\(\hat{\bf w}\)
对时刻\(t = 0, 1, \cdots\)
随机寻找一个\({\bf w}_t\)错分的样本\(({\bf x}_{n(t)}, y_{n(t)})\)
试图通过如下方法修正\({\bf w}_t\) \[ {\bf w}_{t+1} \leftarrow {\bf w}_t + y_{n(t)}{\bf x}_{n(t)} \]
如果\({\bf w}_{t+1}\)犯的错误比\(\hat{\bf w}\)少,那么将\(\hat{\bf w}\)替换为\({\bf w}_{t+1}\)
直到足够多次迭代完成。我们将\(\hat{\bf w}\)(称为\({\bf w}_{\rm pocket}\))返回为\(g\)
注意在线性可分集合上也可以使用口袋法,算法也可以返回一个无训练误差的解。但是由于每次更新权重以后,都要在所有数据上使用新旧权重各跑一遍,来计算错分数量,因此口袋法的执行时间通常比原始PLA的计算时间长很多
